0.前言

从本博客开始,以菜菜九天的深度学习课为基础,从零开始学习深度学习,好好地把握知识点,让自己学有所成.

1.单层神经网络

1.1 单层神经网络基础(线性回归算法)

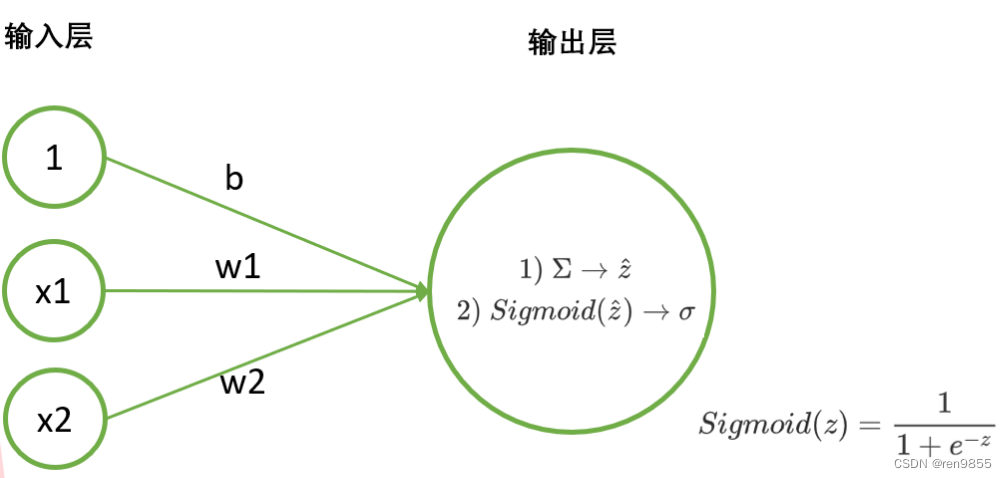
    神经网络是模仿人类大脑结构所构建的算法,在人脑里,我们有轴突连接神经元,在算法中,数据从神经网络的左侧输入,让神经元处理之后,从右侧输出结果.如下图所示:

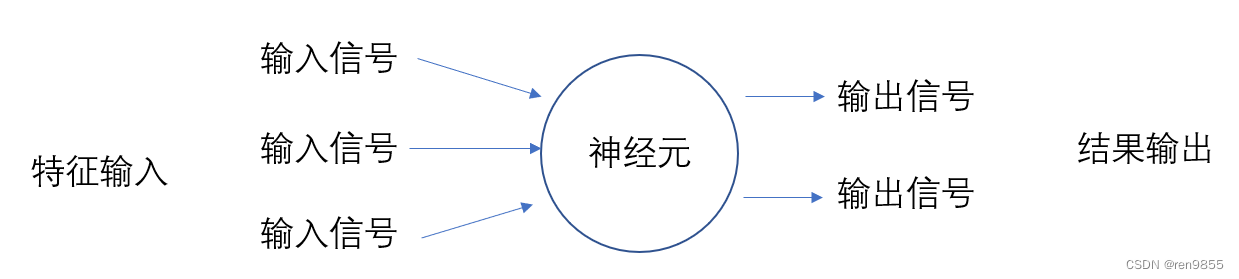
    线性回归算法是机器学习中的回归类算法，多元线性回归指的就是一个样本对应多个特征的线性回归问题。假设我们的数据现在就是二维表，对于一个有特征的样本而言，它的预测结果可以写作一个方程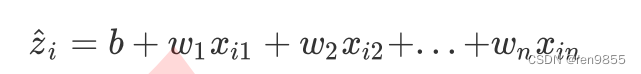：   w和b被统称为模型的权重,其中b被称为截距,也叫做偏差，w₁到w_n被称为回归系数，也叫作权重，x_i1到x_in是样本i上的不同特征。线性回归的任务，就是构造一个预测函数来映射输入的特征矩阵和标签值的线性关系上图的式子转换一下,就变成了单层神经网络:

---

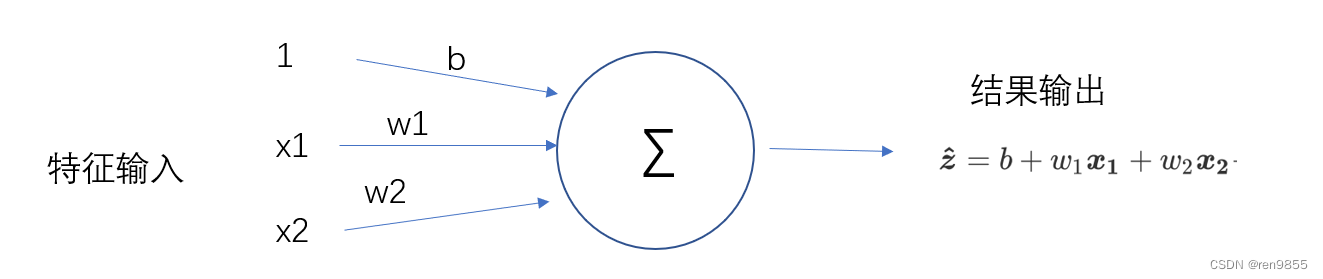
     在上述过程中，左侧的是神经网络的输入层。输入层由众多承载数据用的神经元组成，数据从这里输入，并流入处理数据的神经元中。在所有神经网络中，输入层永远只有一层，且每个神经元上只能承载一个特征或一个常量（通常都是1).
  右侧的是输出层,输出层由大于等于一个神经元组成，我们可以从这一层来获取预测结果。输出层的每个神经元上都承载着单个或多个功能，可以处理被输入神经元的数据。在线性回归中，这个功能就是“加和”，当我们把加和替换成其他的功能，就能够形成各种不同的神经网络.

1.2 torch.nn.Linear实现单层回归神经网络的正向传播

特征和标签数据如下所示:

x0	x1	x2	Y
1	0	0	-0.2
1	1	0	-0.05
1	0	1	-0.05
1	1	1	0.1

import torch

X = torch.tensor([[0,0],[1,0],[0,1],[1,1]], dtype = torch.float32)

output = torch.nn.Linear(2,1)

# output.weight #查看生成的w
# output.bias #查看生成的b
# output = torch.nn.Linear(2,1,bias=False) //如果我们希望不拟合常量b，在实例化时将参数bias设置为False即可

# torch.random.manual_seed(420) #人为设置随机数种子

zhat = output(X)

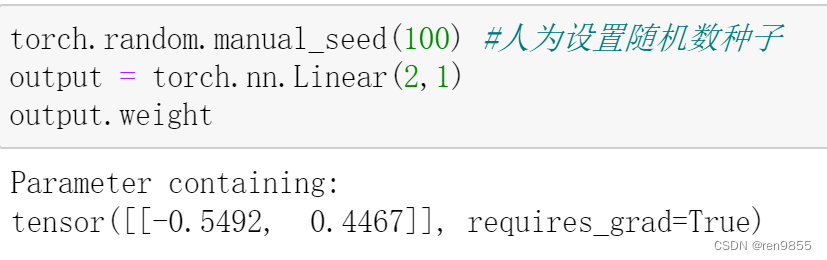
注意事项:

1.nn.Linear需要输入两个参数，分别是（上一层的神经元个数，这一层的神经元个 数）。上一层是输入层，因此神经元个数由特征的个数决定（2个）。这一层是输出层，作为回归神经网络，输出层只有一个神经元。因此nn.Linear中输入的是（2，1）   2.只定义了X，没有定义w和b。所有nn.Module的子类，形如nn.XXX的层，都会在实例化的同时随 机生成w和b的初始值.   3.output.weight #查看生成的w output.bias #查看生成的b   4.torch.random.manual_seed(100) #人为设置随机数种子   5.人为设置随机数种子中间空间的值可以随便填写,设置随机数的目的在于随机生成的W和b会固定下来,不然在调用Linear函数时,每次运行都会产生不同的随机数

2.二分类神经网络：逻辑回归

     线性回归是统计学经典算法，它能够拟合出一条直线来描述变量之间的线性关系。但在实际中，变量之间的关系通常都不是一条直线，而是呈现出某种曲线关系。为了更好的拟合曲线,其中提到了Sigmoid函数,图像如下图:

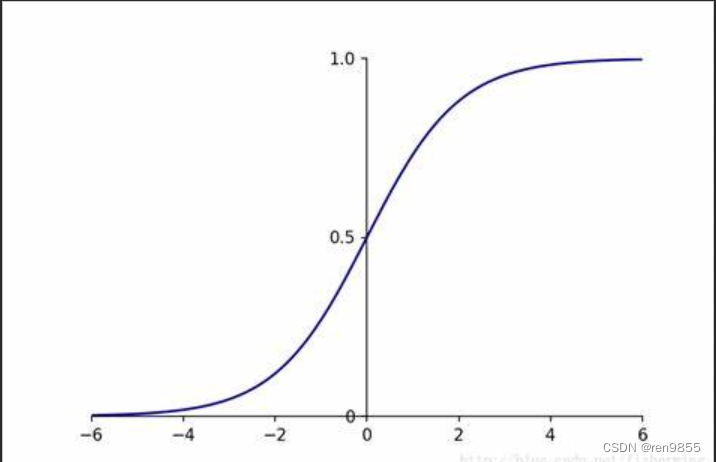
   从图像上就可以看出,当自变量 趋近正无穷时,因变量趋近于1,而当趋近负无穷时， 趋近于0，这使得sigmoid函数能够将任何实数映射到(0,1)区间,让sigmoid函数能够将连续性变量转化为离散型变量，也就是化能够将回归算法转化为分类算法.
   将线性回归方程的结果作为自变量带入sigmoid函数，得出的数据就一定是(0,1)之间的值。此时，只要我们设定一个阈值(比如0.5),规定大于0.5时,预测结果为1类,小于0.5时,预测结果为0类,则可以顺利将回归算法转化为分类算法.此时,我们的标签就是类别0和1了.这个阈值可以自己调整,在没有调整之前,一般默认0.5.

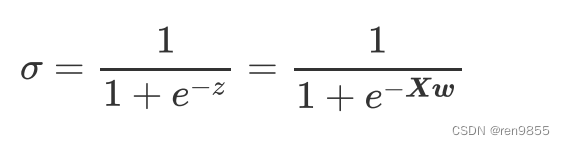
2.1 逻辑回归与门代码实现

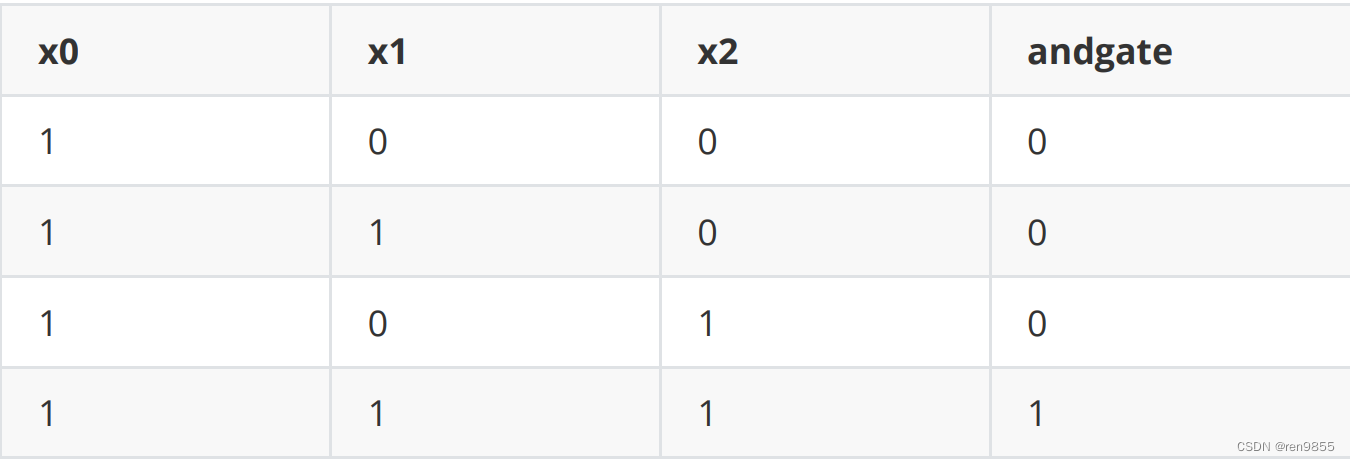
给定特征和标签

import torch

#特征张量X，定义数据类型
X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]], dtype = torch.float32)

#标签Y
andgate = torch.tensor([0,0,0,1], dtype = torch.float32)

#定义w，预定义的一组值,更好的看出结果
w = torch.tensor([-0.2,0.15,0.15], dtype = torch.float32)

def LogisticR(X,w):
    zhat = torch.mv(X,w)  #矩阵与向量相乘得到z
    
    #设置阈值为0.5, 使用列表推导式将值转化为0和1
    andhat = torch.tensor([int(x) for x in sigma >= 0.5], dtype = torch.float32) 
	
    return sigma, andhat

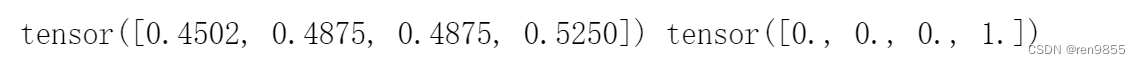
2.2 符号函数

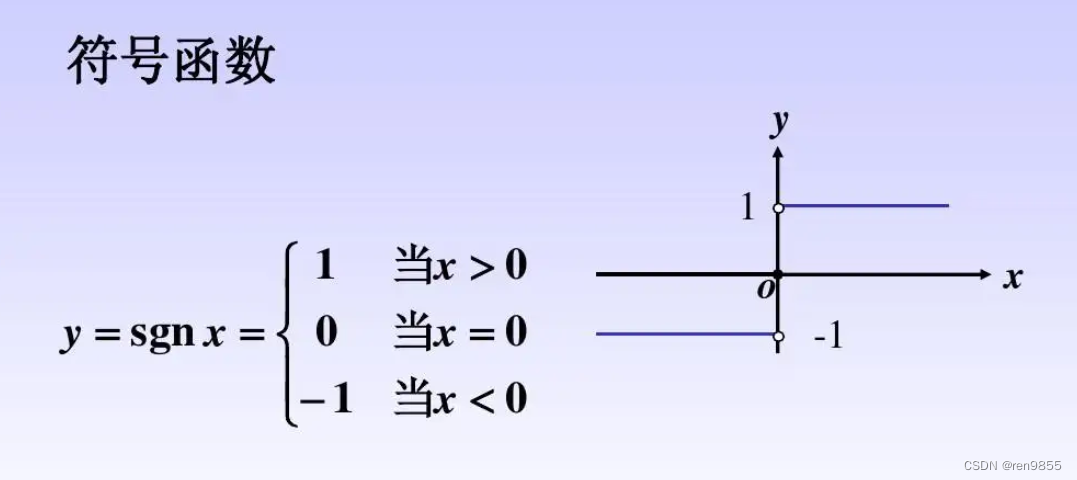
     在上述的代码中,我们知道了Sigmoid实现了将连续型数值转换为分类型数值的作用，除了Sigmoid函数之外，还有许多其他的函数可以被用来将连续型数据分割为离散型数据，如下面的图片所示.

2.2.1 sign函数

2.2.2 Relu函数

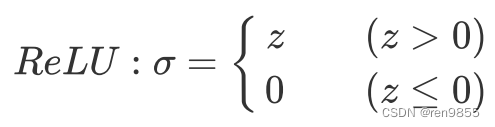
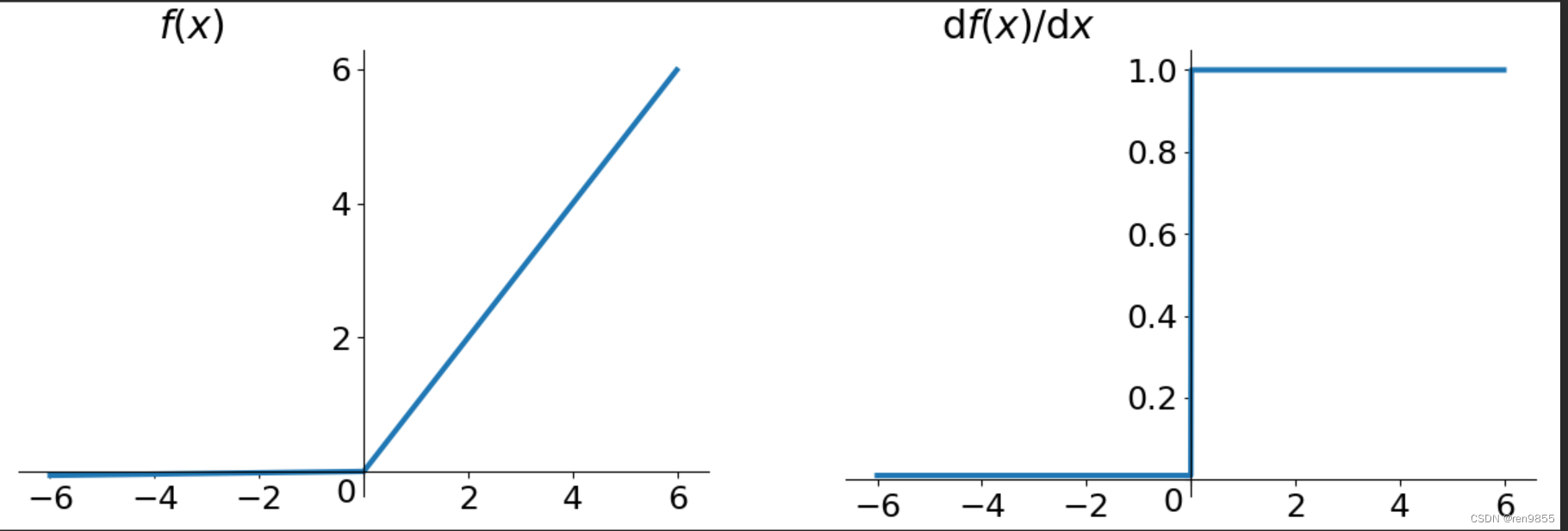
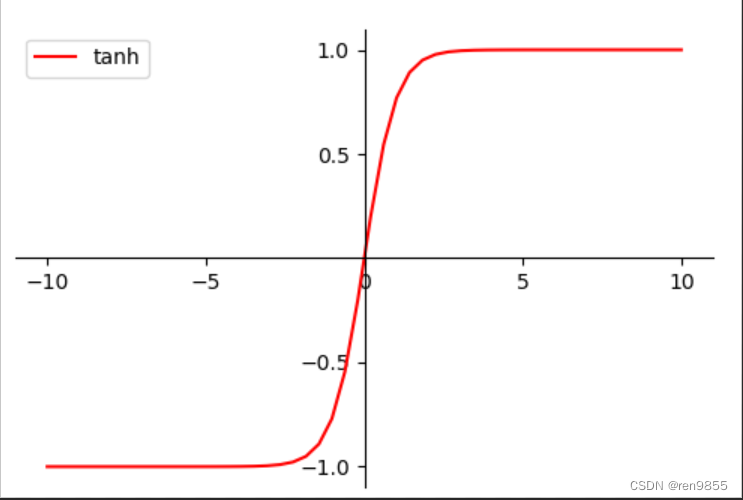
2.2.3 tant函数

3. 多分类神经网络：Softmax回归

    之前介绍分类神经网络时，我们只说明了二分类问题，即标签只有两种类别的问题(0和1,猫和狗,虽然在实际应用中许多分类问题都可以用二分类的思维解决，但依然存在很多多分类的情况.
    最典型的就是手写数字的识别问题。计算机在识别手写数字时，需要对每一位数字进行判断，而个位数字总共有10个,所以手写数字的分类是十分类问题，一般分别用0~9表示。
     真实使用的神经网络往往是一个庞大的算法，建立一个模型就会耗费很多时间，因此必须建立很多个模型来求解的方法对神经网络来说就不够高效,我们有更好的方法来解决这个问题,那就是softmax回归。

     Softmax函数是深度学习的基础，它是神经网络进行多分类时，默认放在输出层中处理数据的函数。假设现在神经网络是用于三分类数据，且三个分类分别是苹果，香蕉和橘子，序号则分别是分类1、分类2和分类3。则使用softmax函数的神经网络的模型会如下所示：

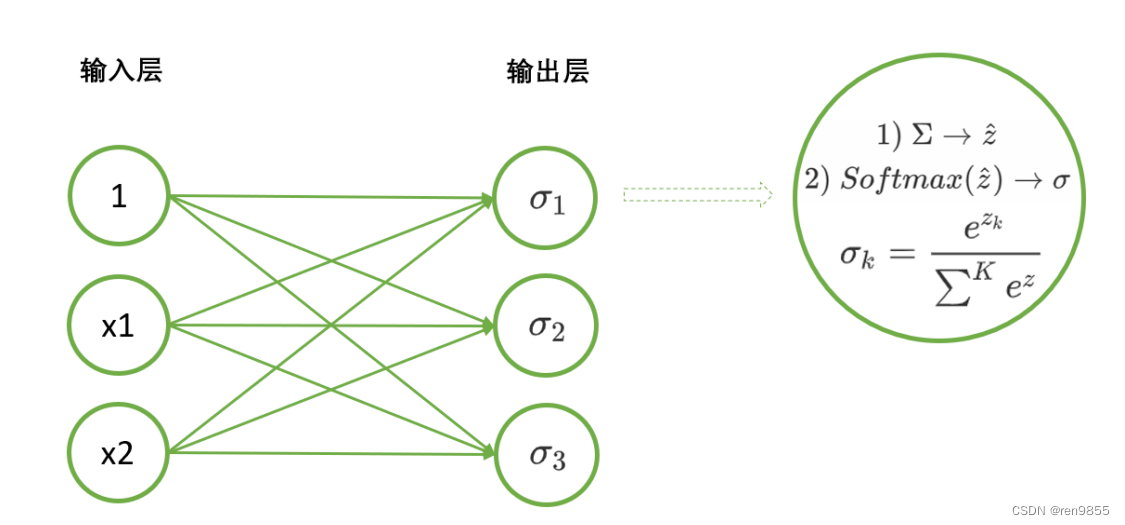
     与二分类一样，我们从左侧输入特征，从右侧输出概率，通过softmax函数来进行计算。softmax的输出层有三个神经元，分别输出该样本的真实标签是苹果和香蕉和橘子的概率 。在多分类中，神经元的个数与标签类别的个数是一致的，如果是十分类，在输出层上就会存在十个神经元，分别输出十个不同的概率。此时，样本的预测标签就是所有输出的概率中最大的概率对应的标签类别。

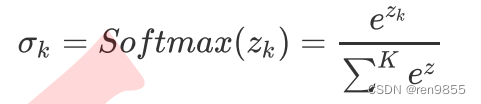
     当我们有三个分类，分别是苹果,橘子和香蕉的时候，样本i被分类为橘子的概率为：