2022-11-20 每日打卡：Leetcode第 320 场周赛

题解主要参考：https://www.bilibili.com/video/BV1A3411f7H3/?spm_id_from=333.999.0.0&vd_source=6fcf135348bf11256bcd756a96851533

6241. 数组中不等三元组的数目

对于排列组合问题，关注“顺序是否影响结果”。这个题目的注意看起来是说顺序会影响结果，但实际上（0，2，4）和（2，0，4）指的就是同一个三元组，而该三元组只能加进去一次。
所以我们就可以【排序+统计】，对于每个相同的数字，比他小的可以选一个，比他大的可以选一个。复杂度O(nlogn)。

class Solution:
    def unequalTriplets(self, nums: List[int]) -> int:
        nums.sort()
        ans = start = 0
        for i in range(len(nums)-1):
            if nums[i]!=nums[i+1]:
                # start 前面可以选的数
                # (i-start+1) 重复的段
                # (len(nums)-1-i) 后面可选的数
                ans += start * (i-start+1) * (len(nums)-1-i)
                start = i+1
        return ans

6242. 二叉搜索树最近节点查询

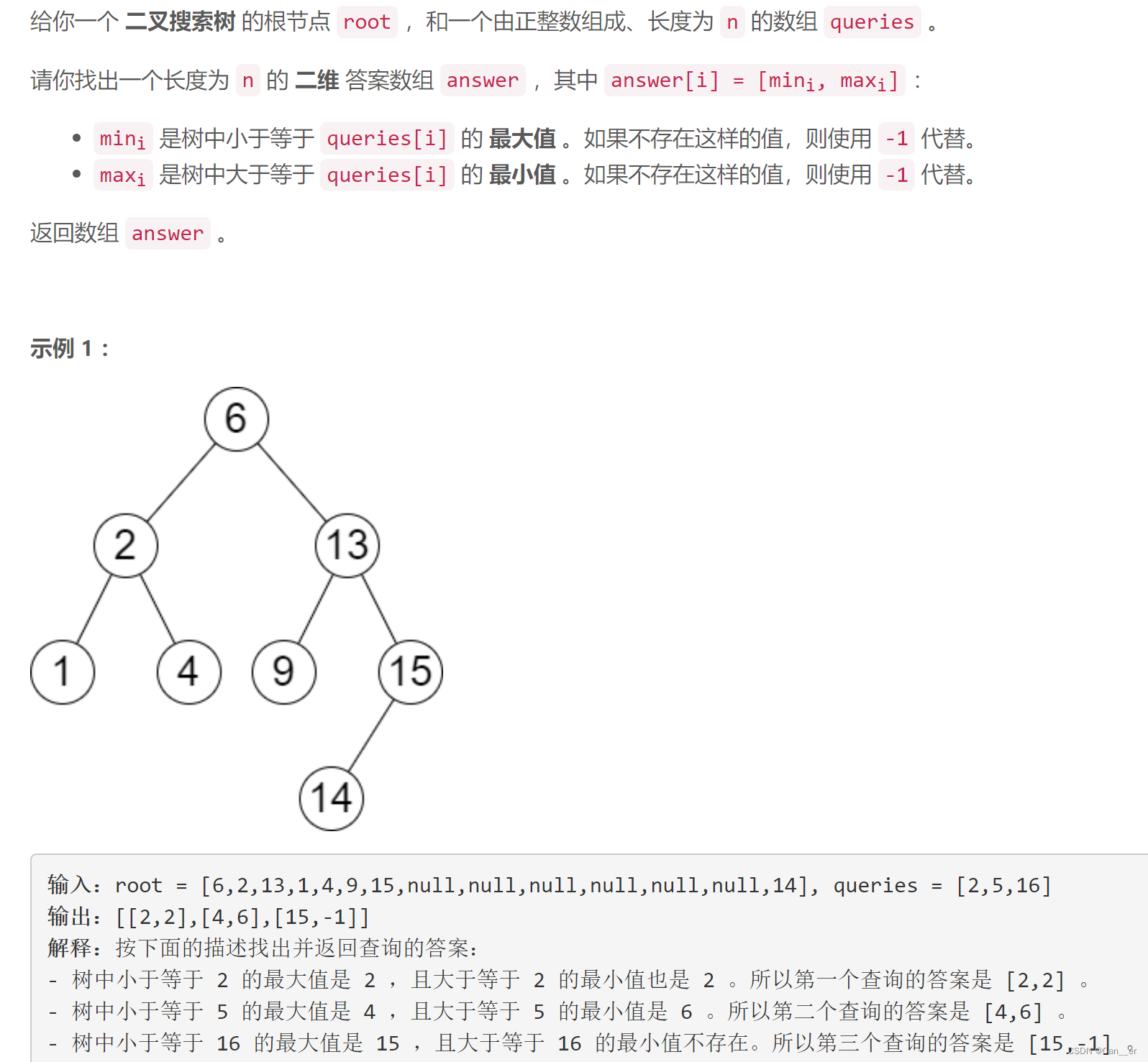
• 最大的是遍历到不能遍历，右走的分支最近的
• 最小的是遍历到不能遍历，左走的分支最近的
• 不要每个结点都去遍历，使用dfs+二分可以快速查找！

class Solution:
    def closestNodes(self, root: Optional[TreeNode], queries: List[int]) -> List[List[int]]:
        nodes = []
        def dfs(node):
            if not node:
                return
            dfs(node.left)
            nodes.append(node.val)
            dfs(node.right)
        dfs(root)
        ans = []
        for q in queries:
            # 把<=转化为>，bisect_right返回相等最右侧元素+1，大于该元素
            min_ = bisect_right(nodes, q)-1
            min = nodes[min_] if min_>=0 else -1
            # >=，bisect_left返回相等最左侧元素，大于该元素
            max_ = bisect_left(nodes, q)
            max = nodes[max_] if max_<len(nodes) else -1
            ans.append([min, max])
        return ans

6243. 到达首都的最少油耗

【无向、连通、无环】，实际上就是各个结点到0号的只有一条边。
而需要的车车数量就是【走过的边//seats】的向上取整。
对于某个边来说，有多少城市代表要走呢？答案是【子树的nodes数目】。
最终，该题转化为，从0开始使用dfs，对每个边而言其子树的nodes数目就是要走的个数。递归的返回给上一层的同时，更新ans即可。

class Solution:
    def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:
        ans = 0
        g = [[] for _ in range(len(roads) + 1)]
        # 双向边必须两个都加
        for x, y in roads:
            g[x].append(y)
            g[y].append(x)
        
        def dfs(x: int, fa: int) -> int:
            # size是子树规模，递归的返回给上一层
            size = 1
            for y in g[x]:
                # 避免陷入循环
                if y != fa:
                    size += dfs(y, x)
            # 0这个结点的子树规模不用算
            # 因为它并不从0出发到0
            if x:
                nonlocal ans
                # 向上取整的技巧
                ans += (size + seats - 1) // seats
            return size
        dfs(0, -1)
        return ans

6244. 完美分割的方案数

如何思考动态规划？

1. 有哪些变量？
2. 替换变量名，复述问题。
3. 最后一步发生什么？通过思考最后一步来分解任务。
4. 去掉最后一步，问题规模缩小。
5. 得到状态转移方程。

本题变量，分割的个数i，字符串长度j。

把一个长为 j 的字符串，分割出i段的合法方案数。

最后一步是分割出 一个子串，长度为 x ，且这个字串是 s 的后缀。

去掉最后一步，子问题变成：
把一个长为 j-x 的字符串，分割出 i-1 段的合法方案数。

从第二部的问题描述中，【把一个长为 j 的字符串，分割出i段的合法方案数】可以写出 f[i][j]。真正的代码实现时，把分割个数写到外面一层比较方便，可以从小的分割个数转移到大的分割个数。
取不同的x，可以得到不同的方案数，所以关系是求和。

$f[i][j]=\sum f[i-1][j-x]=\sum f[i-1][j^{\prime }]$

这里满足 $j^{\prime }$ 是第 $i$ 段的开始下标。

• 满足长度，$j-j^{\prime }+1>=minLength$
• 满足要求，$s[j^{\prime }]$ 是质数而 $s[j]$ 不是质数

寻找初始值：空串分割为0个字串是1个合法的方案，即$f[0][0]=1$

class Solution:
    def beautifulPartitions(self, s: str, k: int, minLength: int) -> int:
        # 看到10^9+7，考虑【动态规划】
        MOD = 10 ** 9 + 7
        def is_prime(c: str) -> bool:
            return c in "2357"

        # 判断是否可以在 j-1 和 j 之间分割（开头和末尾也算）
        def can_partition(j: int) -> bool:
            return j == 0 or j == s_len or not is_prime(s[j - 1]) and is_prime(s[j])

        # 剪枝：长度超了，第一个字母不是质数或最后一个是质数
        s_len = len(s)
        if k * minLength > s_len or not is_prime(s[0]) or is_prime(s[-1]):  
            return 0

        # 从字符串长度0，分割0段开始
        f = [[0] * (s_len + 1) for _ in range(k + 1)]
        f[0][0] = 1
        for i in range(1, k + 1):
            sum = 0
            # 枚举的起点前面一定有 i * minLength 的长度
            # 枚举的终点后面一定有 (k-i) * minLength 的长度
            for j in range(i*minLength, s_len - (k-i)*minLength + 1):
                # j'=j-minLength 双指针，枚举j的同时枚举了j'
                if can_partition(j - minLength): 
                    sum = (sum + f[i - 1][j - minLength]) % MOD  
                if can_partition(j): 
                    f[i][j] = sum
        return f[k][s_len]