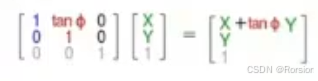方法一：二分答案（+ 位运算集合）

class Solution {
public:
    // 二分答案 顶多O(NlogN),logn去找最后的答案, n用来确定本次找的答案是否正确
    int maxPointsInsideSquare(vector<vector<int>>& points, string s) {
        int res = 0;
        auto check = [&](long long m) -> bool{    // 传入的m是边长, 如果合法返回点数
            unordered_set<char> hash;   // hash.clear();
            bool fg = true;             
            for(int i = 0; i < points.size(); i ++){
                // 如果在正方形中就将对应标识加入到set中（并检查set中是否已经重复）
                int x = points[i][0], y = points[i][1];
                if(x <= m / 2 && x >= -m / 2 && y <= m / 2 && y >= -m / 2){
                    if(hash.count(s[i])){
                        fg = false;
                        break;
                    }else
                        hash.insert(s[i]);
                }
            }
            if (fg) {
                res = hash.size();  
                return fg;  // 不要直接return hash.size()否则有可能为0会与fg=0的情况搞混...
            }
            return fg;
        };
        long long l = 0, r = 2e9;     // 边长的最大值
        while (l < r){
            long long mid = (l + r + 1) >> 1;   // 可能会爆int,比如l=1e9,r=2e9就爆了
            if(check(mid))  l = mid;
            else            r = mid - 1;
        }
        return res;
    }
};

0x3f针对我代码set的优化（位运算）

auto check = [&](int size) -> bool {
            int vis = 0;
            for (int i = 0; i < points.size(); i++) {
                // 判断点是否在正方形中
                if (abs(points[i][0]) <= size && abs(points[i][1]) <= size) {
                    char c = s[i] - 'a';
                    if (vis >> c & 1) { // c 在集合中
                        return false;
                    }
                    vis |= 1 << c; // 把 c 加入集合
                }
            }
            ans = __builtin_popcount(vis);
            return true;

方法二：维护次小距离的最小值

“针对每个字符维护出最小的距离，在遍历的过程中，维护出全局最小的“次小切比雪夫距离””，这对于确定最多有几个合法点至关重要。

class Solution {
public:
    int maxPointsInsideSquare(vector<vector<int>>& points, string s) {
        vector<int> min1(26, 1e9 + 1);  // 最小切比雪夫距离
        int min2 = 1e9 + 1;             // 全局最小的"次小切比雪夫距离"
        int res = 0;
        for(int i = 0; i < points.size(); i ++){
            int x = points[i][0], y = points[i][1], c = s[i] - 'a';
            int d = max(abs(x), abs(y));
            if(d < min1[c]){
                min2 = min(min2, min1[c]);  // 该字符的最小切比雪夫距离已经更新,min2也应该检查更新
                min1[c] = d;                // 更新最小切比雪夫距离
            }else if(d < min2){             // 进入次循环，说明距离不会更新到最小min1,但还是有可能会更新到min2
                min2 = min(min2, d);
            }    
        }
        for(int i = 0; i < 26; i ++)
            if(min1[i] < min2)  res ++;
        return res;
    }
};