【算法中的数学】欧拉筛埃氏筛

news2025/4/4 14:43:00

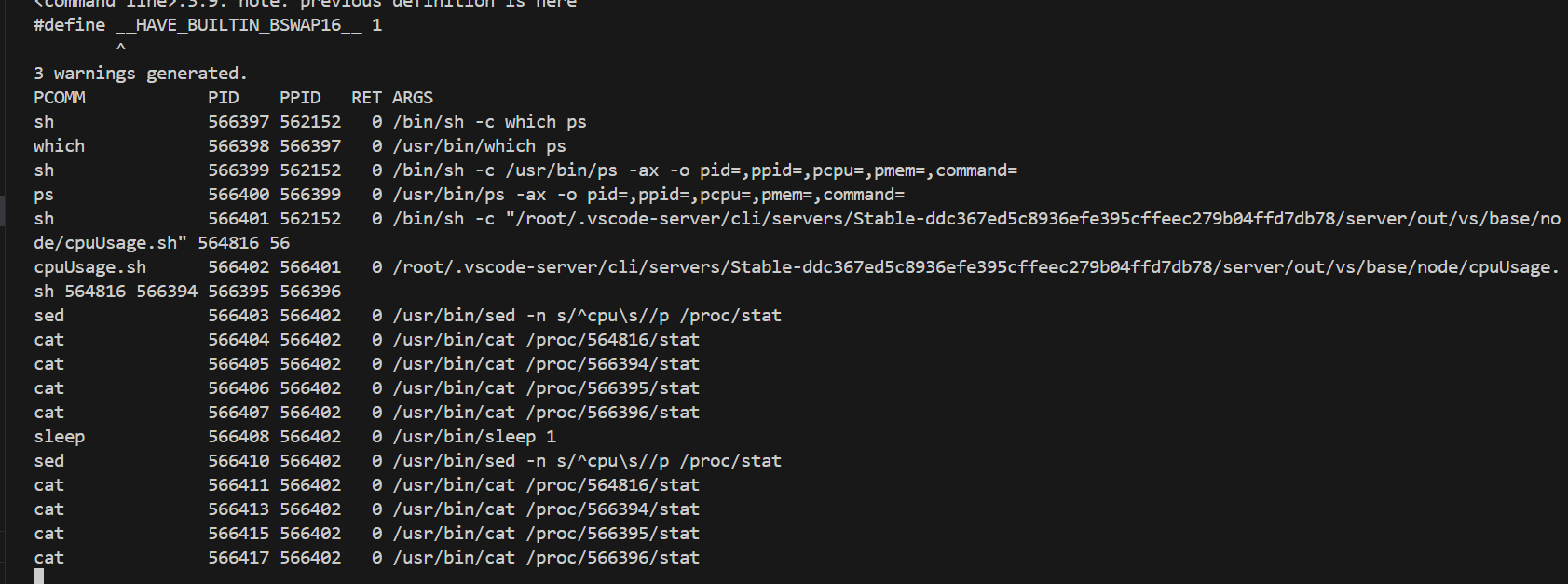
筛质数

题目传送门

题目链接

一、题目描述

给定一个正整数 n，请你求出 1∼n 中质数的个数。

输入格式
共一行，包含整数 n。

输出格式
共一行，包含一个整数，表示 1∼n 中质数的个数。

数据范围
1 ≤ n ≤ 10⁶

输入样例：

输出样例：

二、题目分析

我们需要统计从1到n之间的所有质数的数量。质数是指大于1的自然数，除了1和它本身外没有其他约数。

三、解题思路

这道题有两种常见的筛法可以高效解决：

埃拉托斯特尼筛法（埃氏筛）：从2开始，将每个质数的倍数都标记为合数
欧拉筛（线性筛）：每个合数只会被它的最小质因数筛掉，时间复杂度更低

四、算法讲解

1. 埃氏筛法

初始化一个布尔数组st，表示数字是否被筛掉
从2开始遍历：
- 如果当前数未被筛掉，则它是质数，计数器加1
- 然后将其所有倍数标记为合数
时间复杂度：O(n log log n)

例子：n=8

2是质数，筛掉4,6,8
3是质数，筛掉6(已被筛过)
4被筛过
5是质数，筛掉10(超过n)
6被筛过
7是质数
8被筛过
最终质数：2,3,5,7共4个

2. 欧拉筛法

维护一个质数数组prime
同样从2开始遍历：
- 如果当前数未被筛掉，加入质数数组
- 对于每个质数prime[j]，筛掉i*prime[j]
- 当i能被prime[j]整除时停止，保证每个数只被最小质因数筛掉
时间复杂度：O(n)

例子：n=8

i=2: 加入prime, 筛4
i=3: 加入prime, 筛6,9(9>n停止)
i=4: 筛8(4%2==0停止)
i=5: 加入prime
i=6: 筛12(>n)
i=7: 加入prime
i=8: 筛16(>n)
同样得到4个质数

五、代码实现

#include <bits/stdc++.h>
using namespace std;
// #define int long long
const int N = 1e6 + 10;
int n, cnt;
int prime[N];
bool st[N];

// 埃氏筛
void aishi()
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i])
        {
            prime[cnt++] = i;
            st[i] = true;
            // 将 i 的倍数全部筛掉
            for (int j = i * 2; j <= n; j += i)
            {
                st[j] = true;
            }
        }
    }
}

// 欧拉筛
void oula()
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i])
        {
            prime[cnt++] = i;
        }
        for (int j = 0; prime[j] * i <= n; j++)
        {
            st[i * prime[j]] = true;
            if (i % prime[j] == 0)  // 被最小的指数筛
                break;
        }
    }
}

void solve()
{
    cin >> n;
    // aishi();
    oula();
    cout << cnt << "\n";
}
signed main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    solve();
    return 0;
}