引言

在机器学习中，代价函数（Cost Function）是一个用于衡量模型预测值与实际值之间差异的函数。在监督学习中，代价函数是评估模型性能的关键工具，它可以帮助我们了解模型在训练数据上的表现，并通过优化过程来改善模型

二、实现用Jupyter Notebook并探索单变量线性回归的代价函数

2.1 工具

在这个实验室中使用：

• NumPy，一个流行的科学计算库
• Matplotlib，一个流行的数据绘图库
• 本地目录中的 lab_utils_uni.py 文件中的本地绘图例程

import numpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from lab_utils_uni import plt_intuition, plt_stationary, plt_update_onclick, soup_bowl
plt.style.use('./deeplearning.mplstyle')

2.2 问题陈述

希望有一个模型，可以根据房屋的大小预测房价。
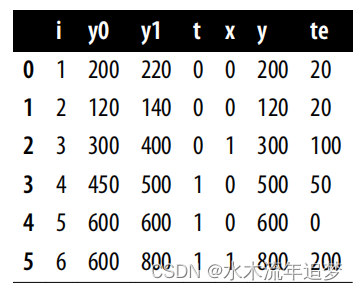
使用的两个数据点:一个1000平方英尺的房子以30万美元的价格售出，一个2000平方英尺的房子以50万美元的价格售出。

尺寸 (1000 sqft)	价格 (10万美元)
1.0	300
2.0	500

• x_train = np.array([1.0, 2.0]) # (尺寸，以1000平方英尺为单位)
• y_train = np.array([300.0, 500.0]) # (价格，以1000美元为单位)

2.3 计算成本

在这里，成本是衡量模型在预测房屋目标价格方面表现如何的度量，对于房屋数据，“价格”一词被使用
单变量成本方程是：

其中 𝑓𝑤,𝑏(𝑥(𝑖))=𝑤𝑥(𝑖)+𝑏(2)

• 𝑓𝑤,𝑏(𝑥(𝑖))是使用参数 𝑤,𝑏 对示例 𝑖 的预测
• (𝑓𝑤,𝑏(𝑥(𝑖))−𝑦(𝑖))2是目标值和预测值之间的平方差
• 这些差异被加总，然后除以 2m 来产生成本 𝐽(𝑤,𝑏)

注意，求和范围通常是从1到m，而代码将从0到m-1
下面的代码通过遍历每个示例来计算成本。在每个循环中：$f_{w}b$，一个预测被计算
目标值和预测值之间的差异被计算并平方，这被加到总成本中

def compute_cost(x, y, w, b): 
    """
    计算线性回归的代价函数。
    
    参数:
      x (ndarray (m,)): 数据，m个示例
      y (ndarray (m,)): 目标值
      w,b (标量)    : 模型参数
    
    返回:
        total_cost (float): 使用w,b作为线性回归参数来拟合x和y中的数据点的成本
               to fit the data points in x and y
    """
    # 训练示例的数量
    m = x.shape[0] 
    
    cost_sum = 0 
    for i in range(m): 
        f_wb = w * x[i] + b   
        cost = (f_wb - y[i]) ** 2  
        cost_sum = cost_sum + cost  
    total_cost = (1 / (2 * m)) * cost_sum  
    return total_cost

2.4 代价函数直观

目标是找到一个模型 𝑓𝑤,𝑏(𝑥)=𝑤𝑥+𝑏，其中参数 𝑤,𝑏 可以准确预测房屋的价值。代价是衡量模型在训练数据上的准确性的度量。

上述的成本方程显示，如果 𝑤 和 𝑏 可以选择，使得预测 𝑓𝑤,𝑏(𝑥)与目标数据 $y$ 匹配，那么 $(f_{w,b}(x^{(i)})-y^{(i)}{)}^2$ 项将变为零，成本最小化
在之前的实验室中，你确定 $b=100$ 提供了最优解，所以让我们将 $b$ 设置为 100，并专注于 $w$
下面，使用滑块控制来选择最小化成本的 $ w $ 值。更新图形可能需要几秒钟，如下图所示：

plt_intuition(x_train, y_train)

该图包含几个值得注意的点

• 成本在 $ w = 200 $ 时最小化，这与之前的结果相匹配
• 由于成本方程中目标值和预测值之间的差异被平方，当 $ w $ 太大或太小时，成本会迅速增加
• 使用通过最小化成本选择的 $ w $ 和 $ b $ 值，可以得到一条完美符合数据的直线

2.5 代价函数可视化 - 3D

可以通过在 3D 中绘制或在使用等高线图来查看成本如何随着 $w$ 和 $b$ 的变化而变化

2.6 更大的数据集

查看包含更多数据点的场景是有益的。这个数据集包括不在同一直线上的数据点。这对成本方程意味着什么？我们能找到 $ w $ 和 $ b $，使成本为 0？

x_train = np.array([1.0, 1.7, 2.0, 2.5, 3.0, 3.2])
y_train = np.array([250, 300, 480,  430,   630, 730,])

在等高线图中，点击一个点来选择 $w$ 和 $b$ 以达到最低成本。使用等高线来指导你的选择。注意，更新图形可能需要几秒钟。

plt.close('all') 
fig, ax, dyn_items = plt_stationary(x_train, y_train)
updater = plt_update_onclick(fig, ax, x_train, y_train, dyn_items)

在上方，请注意左侧图中的虚线。这些代表了训练集中每个示例对成本的贡献。在这种情况下，大约 $w=209$ 和 $b=2.4$ 提供低成本。请注意，由于我们的训练示例不在同一直线上，最低成本不为零

2.7 凸成本表面

成本函数将损失平方的事实确保了“误差表面”像汤碗一样是凸的。它总是通过在所有维度上跟随梯度来达到最小值。在之前的图中，由于 $ w $ 和 $ b $ 的维度不同，这不容易识别。在展示的下一个图中，$w$ 和 $b$ 是对称的：

soup_bowl()

2.8 总结

• 成本方程提供了衡量你的预测与训练数据匹配程度的度量
• 最小化成本可以提供 $w$ 和 $b$ 的最优值

三、遇到的问题

3.1 没有ipympl第三方库

3.1.1 问题

报错：

ModuleNotFoundError: No module named ‘ipympl’

3.1.2 解决方法

添加一个单元格，安装对应算法包，因为我是conda启动，所以用conda的安装命令，安装完即可

3.2 运行matplotlib代码没有显示图片

3.2.1 问题

报错：

[Open Browser Console for more detailed log - Double click to close this message]
Failed to load model class ‘MPLCanvasModel’ from module ‘jupyter-matplotlib’
Error: Script error for “jupyter-matplotlib”
http://requirejs.org/docs/errors.html#scripterror
at makeError (http://localhost:8888/static/components/requirejs/require.js?v=d37b48bb2137faa0ab98157e240c084dd5b1b5e74911723aa1d1f04c928c2a03dedf922d049e4815f7e5a369faa2e6b6a1000aae958b7953b5cc60411154f593:168:17)
at HTMLScriptElement.onScriptError (http://localhost:8888/static/components/requirejs/require.js?v=d37b48bb2137faa0ab98157e240c084dd5b1b5e74911723aa1d1f04c928c2a03dedf922d049e4815f7e5a369faa2e6b6a1000aae958b7953b5cc60411154f593:1735:36)

3.2.2 解决方法

清空浏览器缓存，关闭Jupyter Notebook，并重新打开即可