线性回归算法应该是大多数人机器学习之路上的第一站,因为线性回归算法原理简单清晰,但却囊括了拟合、优化等等经典的机器学习思想。
说到线性回归,我们得先说说回归与分类、线性与非线性这些概念的区别。
一 分类与回归的区别
机器学习中的分类和回归是两种主要的预测性监督学习任务,它们的主要区别在于输出变量(目标变量)的类型以及模型如何进行预测。
1.1 分类 (Classification)
- 输出类型:分类问题的输出是一个离散的类别或标签。例如,预测一封邮件是否为垃圾邮件(是/否),或者识别一张图片中的人脸是谁(类别A、类别B、类别C等)。
- 模型目标:分类模型的目标是学习一个决策边界,能够将输入数据映射到一个具体的类别上。常见的分类算法有逻辑回归、支持向量机、决策树、随机森林和神经网络等。
- 评估指标:常用的评估指标包括准确率、精确率、召回率、F1分数和混淆矩阵等。
1.2 回归 (Regression)
- 输出类型:回归问题的输出是一个连续值。例如,预测房价、股票价格或者温度变化等。
- 模型目标:回归模型的目标是学习一个函数,这个函数能够根据输入特征预测出一个连续值结果。常见的回归算法有线性回归、岭回归、Lasso回归、弹性网回归、决策树回归和神经网络等。
- 评估指标:常用的评估指标包括均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAE)和R²分数等。
1.3 主要区别
- 预测目标:分类预测的是类别,而回归预测的是数值。
- 损失函数:分类问题通常使用如交叉熵损失函数,而回归问题则可能使用平方损失或绝对值损失。
- 输出空间:分类的输出空间是有限且离散的,而回归的输出空间通常是无限且连续的。
在实际应用中,选择分类还是回归取决于问题的性质和目标变量的类型。
二 线性与非线性的区别
2.1 线性回归 (Linear Regression)
定义:线性回归是一种回归模型,它假设自变量与因变量之间的关系可以用一条直线(或在多变量情况下是超平面)来表示。数学上表示如下:
y = β 0 + β 1 x 1 + β 2 x 2 + . . . + β n x n + ϵ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n + \epsilon y=β0+β1x1+β2x2+...+βnxn+ϵ
其中, y y y 是因变量, β 0 \beta_0 β0是截距项, β i \beta_i βi 是自变量 x i x_i xi 的系数, ϵ \epsilon ϵ 是随机误差项。
特点:
-
线性回归模型中的“线性”指的是模型参数与自变量的关系是线性的。
-
当自变量与因变量之间大致呈线性关系时,线性回归是最直接的选择。
2.2 非线性回归 (Nonlinear Regression)
定义:非线性回归模型用于描述自变量与因变量之间复杂、非线性的关系。非线性模型具有更复杂的函数形式,如指数、幂次、三角函数等。
特点
- 非线性回归模型的参数与自变量之间的关系是非线性的,需要通过迭代算法来估计参数。
- 当数据呈现出明显的非线性趋势时,非线性回归模型能更好地捕捉这种趋势。
2.3 主要区别
- 模型形式: 线性回归模型输出是自变量的线性组合;非线性回归模型输出涉及自变量的非线性组合。
- 参数估计: 线性回归模型参数可通过解析解求得;非线性回归模型参数需通过数值优化方法迭代求解。
- 灵活性与复杂度: 非线性回归提供了更大灵活性,但也意味着模型可能更难理解,同时计算成本更高。
三 线性回归的适用条件
那到底什么时候可以使用线性回归呢?
统计学家安斯库姆给出了四个数据集,被称为安斯库姆四重奏。
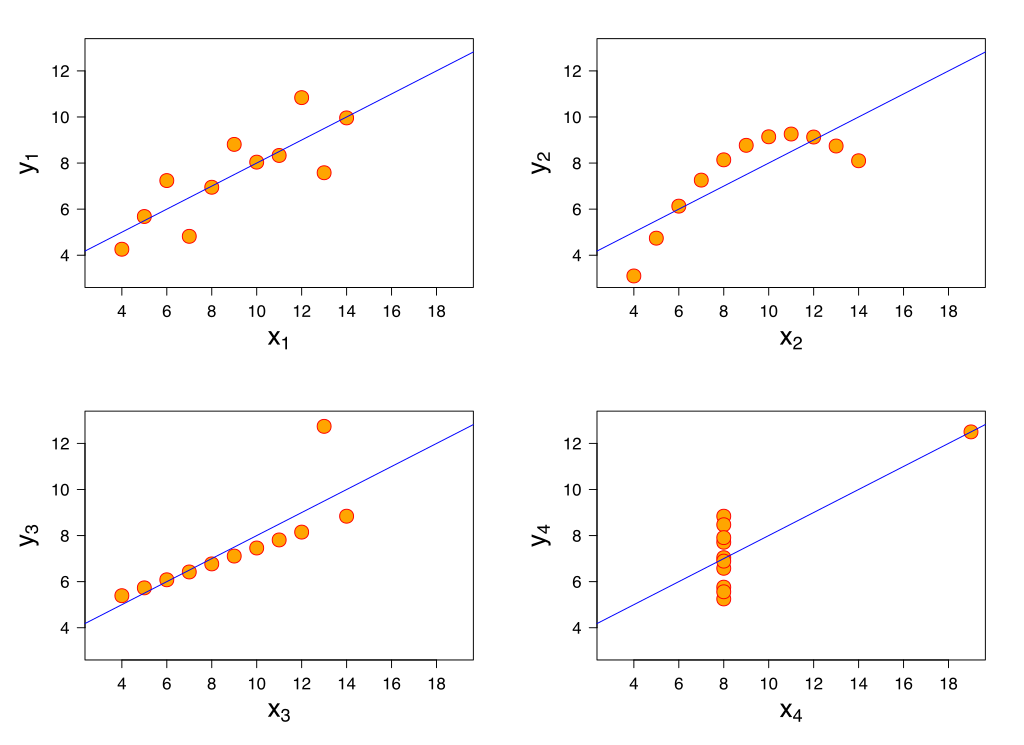
从这四个数据集的分布可以看出,并不是所有的数据集都可以用一元线性回归来建模。现实世界中的问题往往更复杂,变量几乎不可能非常理想化地符合线性模型的要求。因此使用线性回归,需要遵守如下假设。
3.1 线性回归是一个回归问题
与回归相对的是分类问题,分类问题要预测的变量 y 输出集合是有限的,预测值只能是有限集合内的一个。当要预测的变量 y 输出集合是无限且连续,我们称之为回归。比如,天气预报预测明天是否下雨,是一个二分类问题;预测明天的降雨量多少,就是一个回归问题。
3.2 变量之间是线性关系
线性通常是指变量之间保持等比例的关系,从图形上来看,变量之间的形状为直线,斜率是常数。这是一个非常强的假设,数据点的分布呈现复杂的曲线,则不能使用线性回归来建模。可以看出,安斯库姆四重奏右上角的数据就不太适合用线性回归的方式进行建模。
3.3 误差服从均值为零的正态分布
误差可以表示为:误差 = 实际值 - 预测值。
可以这样理解这个假设:线性回归允许预测值与真实值之间存在误差,随着数据量的增多,这些数据的误差平均值为0;
从图形上来看,各个真实值可能在直线上方,也可能在直线下方,当数据足够多时,各个数据上上下下相互抵消。如果误差不服从均值为零的正态分布,那么很有可能是出现了一些异常值。
3.4 变量x的分布要有变异性
线性回归对变量x也有要求,要有一定变化,不能绝大多数数据都分布在一条竖线上。
3.5 多元线性回归不同特征之间相互独立
如果不同特征不是相互独立,那么可能导致特征间产生共线性,进而导致模型不准确。
举一个比较极端的例子,预测房价时使用多个特征:房间数量,房间数量*2,-房间数量等,特征之间是线性相关的,如果模型只有这些特征,缺少其他有效特征,虽然可以训练出一个模型,但是模型不准确,预测性差。
四 从GLM的角度看线性回归的基本假设

广义线性模型详解请看: 广义线性模型(1)广义线性模型详解
五 模型参数求解
根据上面的讨论,我们已经熟悉了线性回归模型的形式,接下来讨论怎么求出模型中的参数。
5.1 极大似然估计

5.2 最小二乘法
最小二乘法详细介绍可查看如下文章:
- 最小二乘法简介
- 普通最小二乘法推导证明

可以直接根据公式计算出 θ \theta θ,还是很方便的。不过极大似然估计和最小二乘法的这种解方程组的方式有一定的局限性:
- 最严重的就是,如果这个方程组是没有解的,那么这种求解方法就是完全没法用的;
- 再者,对于X的维度非常高的时候,直接求解是非常困难的,时间复杂度也非常的高。
因此我们需要更通用、高效的参数求解方法:梯度下降法。
5.3 梯度下降法
梯度下降法详细介绍请查看文章:梯度下降法
使用梯度下降来求解参数:
θ = θ − α X T ( X θ − Y ) \mathbf\theta= \mathbf\theta - \alpha\mathbf{X}^T(\mathbf{X\theta} - \mathbf{Y}) θ=θ−αXT(Xθ−Y)
通过不断的迭代,在达到我们设置的中止条件之后,我们就可以认为找到了最优的参数 θ \theta θ了,这种方法即通用,效率又高,效果非常好,谁用谁知道。
六 总结
本篇主要讨论线性回归的一些基本概念、基本的模型参数求解方法,还有其在广义线性模型体系下的理解方式,下一篇具体讨论下线性回归的一些细节及常用的实现。