目录
Causal Quantities: An Example
Bias
Causal Quantities: An Example
让我们看看在我们的商业问题中,你如何定义这些量。首先,你要注意到,你永远无法知道价格削减(即促销活动)对某个特定商家的确切影响,因为这需要你同时看到两种可能的结果:没有促销时的销售额AmountSold0i与促销后的销售额AmountSold1i。但是,你却可以将焦点放在一些可估算的事情上,比如价格削减对销售额的平均影响:
或是参与价格削减的商家如何增加了它们的销售量:
又或是圣诞节那一周进行促销活动的影响:
现在,我明白你无法同时看到两个可能的结果,但为了论证的目的,也为了让事情变得更为具体,我们假设你能够。想象一下,因果推断的神明对你在众多统计战役中的英勇表现感到满意,因而赐予你神力,使你能看到潜在的替代宇宙——在其中一个宇宙里,每种结果都已发生。凭借这股力量,你说你收集了六个商家的数据,其中三个商家正在进行促销,而另外三个则没有。
在下表中,i是单位标识符,y是观察到的结果,y0和y1分别是控制组和处理组的潜在结果,t是处理指示符,x是标记距离圣诞节还有多少周的协变量。请记住,进行促销是处理,销售金额是结果。我们同样假设在这六个商家中,你从两个商家那里收集到了圣诞节前一周的数据,这通过x=1来表示;而其余的数据则来自圣诞节当周:
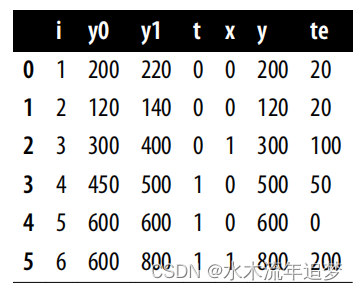
你可能会看着这个数据思考,“这当然不理想,但我不能仅仅取处理组的平均值,然后与未处理组的平均值进行比较吗?换句话说,我不能直接做ATE = (500 + 600 + 800) / 3 - (200 + 120 + 300) / 3 = 426.67吗?”不可以! 你刚刚犯下了将关联误认为因果关系的严重错误!
注意结果的差异有多大。你之前计算的ATE不到100,而现在你却说它是超过400。问题在于,参与促销活动的商家与未参与的商家不同。事实上,即使不降价,参与促销的商家也可能卖出更多的商品。为了证明这一点,只需回顾一下你能看到两种潜在结果的情况。那时,处理组的Y0比未处理组高得多。处理组之间Y0的这种差异使得仅通过比较两组来揭示处理效应变得更加困难。
尽管比较平均值并不是最明智的想法,但我认为你的直觉方向是正确的。现在是时候应用你刚学到的新概念来精炼这一直觉,最终理解为什么关联并不等于因果。是时候面对因果推断的主要敌人了。
Bias
直截了当地说,偏差是让关联与因果产生区别的原因。你在数据中估计的量与你想恢复的因果量不符,这才是问题所在。幸运的是,通过一些直观理解,这个问题很容易被把握。让我们回顾一下商业案例。当你面对“降价能增加商家销售量”的说法时,你可以质疑它,指出那些进行促销的商家即使没有降价,可能也会卖出更多的商品。也许这是因为它们规模更大,有能力实施更具侵略性的促销策略。换句话说,进行促销的商家(即被处理的商家)与未进行促销的商家(即未被处理的商家)不具备可比性。
为了给出更正式的论证,你可以使用潜在结果符号来转化这一直观认识。首先,为了估计ATE,你需要估计如果被处理者没有接受处理会发生什么,即E[Y0|T=1],以及如果未被处理者接受了处理会发生什么,即E[Y1|T=0]。当你比较被处理者和未被处理者的平均结果时,你实际上是在用E[Y|T=0]来估计E[Y0],并用E[Y|T=1]来估计E[Y1]。换句话说,你是在试图通过E[Y|T=t]来恢复E[Yt]。如果两者不匹配,那么像E[Y|T=t]这样的估计器,比如接受处理t的那些个体的平均结果,就会成为E[Yt]的有偏估计。
回归直观理解,你甚至可以利用你对世界运作方式的理解来进一步分析。你可以指出,被处理商家的Y0可能比未处理商家的Y0要大。这是因为有能力进行价格削减的商家,无论是否有价格削减,其销售量往往更高。请花一点时间来消化这个观点。习惯于谈论潜在结果需要一段时间,因为它涉及到推理那些可能发生但并未发生的事件。请再次阅读这一段落,确保你理解了它。