质数想必大家都不陌生
从小学到大
质数的概念:一个数如果除了1和本身之外没有其他的因子,那么这个数被称为质数
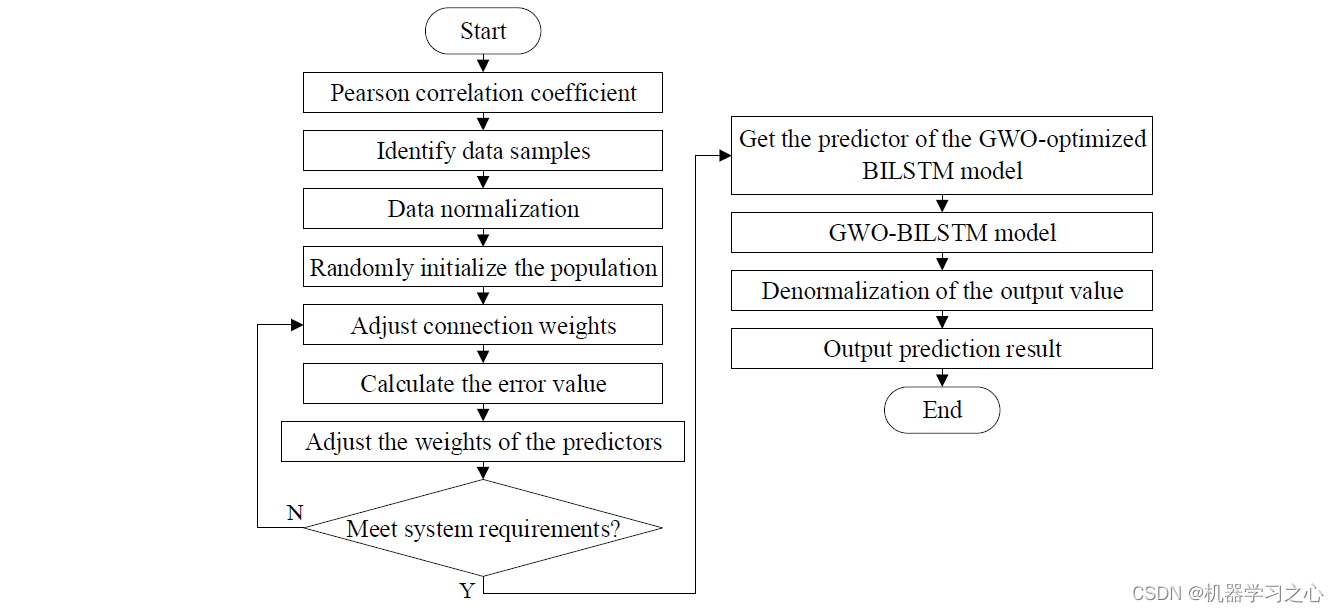
今天要讲两个知识点:
在C++中如何判断一个数是否为质数
在C++中如何判断1-N之间哪些数为整数
- 在C++中如何判断一个数是否为质数
这个知识点较为简单
充分利用上面的概念
我们用一个for循环来解决
因为对于每个数来说,1和n都是他们的因子
所以循环开始为2,终止为n-1
for (int i=2;i<n;i++){
if (n%i==0){
return false;
}
}
return true;But……
时间复杂度也忒高了吧
大概就是O(n)
那如果n>10^9的话,那直接出1秒了
所以还得优化
咱们来举个例子,n=16:
n的因子有
1 2 4 8 16
可以看出,4就像一条分割线,分成了前后两部分
前后一一对应
没错 优化的点找到了
循环前面的部分,如果前面都没有的话,那么后面肯定也没有
那么循环终止条件是什么呢?
4是16的什么数?
因数?
算术平方根!
也就是C++中的sqrt
恭喜你!优化成功
代码就不写了,就是把循环条件的n改成sqrt(n),然后加个cmath头文件
成功把时间复杂度降到O(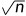 )
)
第一个问题成功解决
- 在C++中如何判断1-N之间哪些数为整数
会不会有一些小伙伴说了
哎哟不就是刚才的刚才的函数调用n编吗?至于单列出来一个标题吗~
NONONONONOONONNOONONONONONO
大错特错
这篇文章的主要就在这里
举个例子,10^9都用不上,咱就说n小于等于10^6,还是很常见的吧
那么时间复杂度就是O(10^6*循环次数)
也就那么亿点点的时间就好了

所以还是那句话,优化优化优化
恭迎今天主角:埃氏筛法!
网友:埃氏筛法 满足你的一切需要!
先讲一下他的思想
思想:
一个合数,一定可以拆成一个质数与另一个数的乘积
每个质数的倍数都是合数
基于以上这两条思想,就可以实现埃氏筛法
用一个数组表示每个数的状态,即是否为质数
循环每个数,如果是质数,就把他所有的倍数全部标为合数
没错就是这么简单
时间复杂度计算方面,我真的很拉
埃氏筛法大概O(n log n)左右吧
(大佬勿喷)
void eratosthemes_prim(int n){
for (int i=2;i<=n;i++){
if_p[i]=true;
}
for (int i=2;i<=n;i++){
if (is_p[i]){
num++;
p[num]=i;//p数组存放质数,num代表目前质数个数
for (int j=i<<1;j<=n;j+=i){
is_p[j]=false;
}
}
}
}这样是不是快了很多?
别走!来看道简简单单的例题
Goldbach's Conjecture
题目描述
全屏
哥德巴赫猜想:任何大于4的偶数都可以拆成两个奇素数之和。 比如:
8=3+5
20=3+17=7+13
42=5+37=11+31=13+29=19+23
你的任务是:验证小于106的数满足哥德巴赫猜想。
输入
多组数据,每组数据一个n。
读入以0结束。
输出
对于每组数据,输出形如n = a + b,其中a,b是奇素数,=和+两边都有空格。若有多组满足条件的a,b,输出b-a最大的一组。
若无解,输出Goldbach's conjecture is wrong.。
样例输入1
8
20
42
0
样例输出1
8 = 3 + 5
20 = 3 + 17
42 = 5 + 37
提示/说明
【数据范围与提示】
对于全部数据,6≤n≤106。
思想:运用埃氏筛法筛出所有数的情况
循环遍历情况即可
# include <iostream>
# include <cstdio>
# include <cstring>
#define N 1000005
using namespace std;
int n,vis[N],flag;
int main(){
memset(vis,0,sizeof(vis));
vis[0]=vis[1]=1;
for(int i=2;i<=N/2;i++){
if(vis[i]==0){
for(int j=2*i;j<=N;j=j+i){
vis[j]=1;
}
}
}
while(scanf("%d",&n)&&n){
flag=0;
for(int i=3;i<=N/2;i++){
if(vis[i]==0&&vis[n-i]==0){
printf("%d = %d + %d\n",n,i,n-i);
flag=1;
break;
}
}
if(flag==0){
printf("Goldbach's conjecture is wrong.\n");
}
}
return 0;
}有些人也许会问
题目里说的是奇素数,可你的代码中没体现出奇数这个条件啊?
问这个问题的,思考一下,偶数可能是素数吗?所以不需要考虑
还有一个问题:陈景润都没证明出哥德巴赫是错的,你还判断一下有必要吗?
这个是可以删除的!
都看到这里了,不点个赞吗?
今天的质数就讲解到这里
欢迎大家关注我
持续更新——