数据结构资料汇编：栈

定义

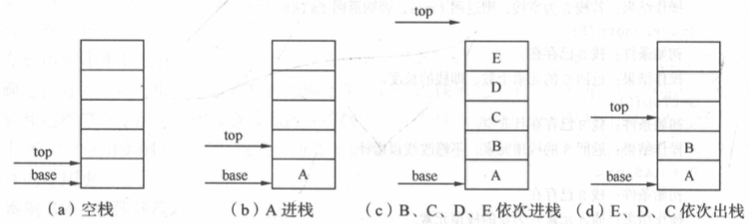
栈（stack）是限定仅在表尾进行插入或删除操作的线性表。

• 表尾称为栈顶（top），可以进行插入或删除操作

  • 栈的插入操作称为 进栈或 入栈（push）
  • 栈的删除操作成为 出栈或 退栈（pop）

• 表头称为栈底（bottom）

• 不含元素的空表称为空栈

• 操作特性：后进先出（Last In First Out，LIFO）

抽象数据类型

ADT Stack {
    数据对象： D = {a_i | a_i in ElemSet, i=1,2,...,n, n<=0}
    数据关系： R = {<a_{i-1}, a_i> | a_{i-1}, a_i in D, i=2,...,n}，约定 a_n 端为栈顶，a_1 端为栈底。
    基本操作：
        InitStack(&S)
            操作结果：构造一个空栈 S
        DestroyStack(&S)
            初始条件：栈 S 已存在
            操作结果：栈 S 被销毁
        ClearStack(&S)
            初始条件：栈 S 已存在
            操作结果：将栈 S 清为空栈
        StackEmpty(S)
            初始条件：栈 S 已存在
            操作结果：若栈 S 为空栈，则返回 true，否则返回 false。
        StackLength(S)
            初始条件：栈 S 已存在
            操作结果：返回 S 的元素个数，即栈的长度。
        GetTop(S)
            初始条件：栈 S 已存在且非空
            操作结果：返回 S 的栈顶元素，不修改栈顶指针。
        Push(&S, e)
            初始条件：栈 S 已存在
            操作结果：插入元素 e 为新的栈顶元素。
        Pop(&S, &e)
            初始条件：栈 S 已存在且非空。
            操作结果：删除 S 的栈顶元素，并用 e 返回其值。
        StackTraverse(S)
            初始条件：栈 S 已存在且非空。
            操作结果：从栈底到栈顶依次对 S 的每个数据元素进行访问
}ADT Stack

栈的存储结构：

• 顺序栈：利用顺序存储结构实现的栈，即利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素，同时附设指针 top 指示栈顶元素在顺序表中的位置。
• 链栈：指采用链式存储结构实现的栈。通常用单链表表示。

顺序栈的存储结构

1. 参考资料 [1] 中关于顺序栈的定义：

# define MAXSIZE 100 //顺序栈存储空间的初始分配量
typedef struct {
    SElemType *base;  //栈底指针
    SElemType *top;   //栈顶指针
    int stacksize;    //栈可用的最大容量
}SqStack;

• base 为栈底指针，初始化完成后，栈底指针 base 始终指向栈底的位置（栈底元素的下边沿），若 base 的值为 NULL ，则表明栈结构不存在。
• top 为栈顶指针，其初始值指向栈底。每当掺入新的栈顶元素时，指针 top 增加 1；删除栈顶元素时，指针 top 减 1。因此，栈空时， top 和 base 的值相等，都指向栈底；栈非空时， top 始终指向栈顶。
• stacksize 指示栈可使用的最大容量。
• 注意区分，参考资料 [1] 中以下表述：

  • 栈顶元素：线性表的最后一个的元素；
  • 栈底元素：线性表的第一个元素；
  • 栈顶：线性表的表尾，即最后一个元素的“后边”。
  • 栈底：线性表的表头，即第一个元素的“前边”。

2. 参考资料 [2] 中关于顺序栈的定义：

# define MaxSize 100 //顺序栈存储空间的初始分配量
typedef struct
{
    ElemType data[MaxSize]; //存放栈中数据元素
    int top;  //栈顶指针，即存放栈顶元素在 data 数组中的下标
}SqStack;

设置顺序栈 s 的栈顶指针初始值 s->top = -1 ，则：

• 栈空的条件： s->top == -1
• 栈满的条件： s->top == MaxSize - 1 （即 data 数组的最大下标）
• 元素 e 进栈：先将栈顶指针 top 增 1，然后将元素 e 放在栈顶指针处
• 出栈操作：先将栈顶指针处的元素取出放在 e 中，然后将栈顶指针减 1

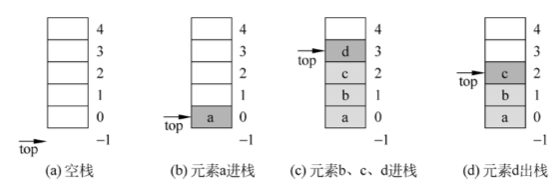
说明：

以上两种定义，本质上是一样的。在第一种定义中，栈 s 的指针 s.base 在对栈进行操作时不变化，因此可以用它指向栈的数据元素。

另外，两种定义内的 s.top 起始值不同，在插入和删除的时候，会有所差异。

顺序栈的基本操作

顺序栈的初始化

使用参考资料 [1] 中的顺序栈数据结构：

//参考资料 [1] 的算法3.1
Status InitStack(SqStack &S){//构造一个空栈 S
    S.base = new SElemType[MAXSIZE];//为顺序栈动态分配一个最大容量为 MAXSIZE 的数组空间
    //S.base=(SElemType *)malloc(MAXSIZE*sizeof(SElemType));
    if(!S.base) exit(OVERFLOW);//存储分配失败
    S.top = S.base; //top 初始值为 base，空栈
    S.stacksize = MAXSIZE;//stacksize 设置为栈的最大容量 MAXSIZE
    return OK;
}

使用参考资料 [2] 中的顺序栈数据结构：

void InitStack(SqStack * &s){
    s = (SqStack *)malloc(sizeof(SqStack));  //分配一个顺序栈空间，首地址存放在 s 中
    s->top = -1;   //栈顶指针置为 -1
}

顺序栈的入栈

//参考资料 [1] 的算法3.2
Status Push(SqStack &S, SElemType e){//插入元素 e 为新的栈顶元素
    if(S.top - S.base == S.stacksize) retuan ERROR; //栈满
    ((*S).top)++ =  e;//元素 e 压入栈顶，栈顶指针加 1。注意顺序，先赋值，再加 1
    return OK;
}

注意此处入栈的操作顺序，先完成 (*S).top = e 赋值，再执行 (*S).top++ 指针加 1。这是由参考资料 [1] 所确定的栈的数据结构决定的，即初始化时：S.top = S.base ，且 S.base 指向数组的第一个，即索引为 0 。

如果使用参考资料 [2] 的数据结构，即初始化时：s.top = -1 （该书中写作 s->top = -1），则入栈的操作是（参考资料 [2] 的 81 页）：

bool Push(SqStack * &s, ElemType e){
    if (s->top == MaxSize-1) return false;  //栈满的情况，即栈上溢出
    s->top++;   //栈顶指针增 1
    s->data[s->top] = e;   //元素 e 放在栈顶指针处
    return true;
}

顺序栈的出栈

//参考资料 [1] 的算法3.3
Status Pop(SqStack &S， SElemType &e){//删除 S 栈顶元素，用 e 返回其值
    if (S.top == S.base) return ERROR;  //栈空
    e = *--S.top;  //栈顶指针减1， 将栈顶元素赋值给 e
    return OK;
}

//参考资料 [2] 的算法
bool Pop(SqStack * &s, ElemType &e){
    if (s->top == -1) return false;  //栈为空的情况，即栈下溢出
    e = s->data[s->top];   //取栈顶元素
    s->top--;    //栈顶指针减 1
    return true;
}

销毁顺序栈

//针对 [1] 的栈结构，来自 [3]
void DestroyStack(SqStack *S)
{ /* 销毁栈S，S不再存在 */
 free((*S).base);
 (*S).base=NULL;
 (*S).top=NULL;
 (*S).stacksize=0;
}

//针对 [2] 的栈结构
void DestroyStack(SqStack * s){
    free(s);
}

判断顺序栈是否为空

//针对 [1] 的栈结构，来自 [3]
Status StackEmpty(SqStack S)
{ /* 若栈S为空栈，则返回TRUE，否则返回FALSE */
 if(S.top == S.base)
  return TRUE;
 else
  return FALSE;
}

//针对 [2] 的栈结构
bool StackEmpty(SqStack * s){
    return (s->top == -1);
}

读取顺序栈的栈顶元素

//针对 [1] 的栈结构，来自 [3]
Status GetTop(SqStack S,SElemType *e)
{ /* 若栈不空，则用e返回S的栈顶元素，并返回OK；否则返回ERROR */
 if(S.top > S.base)
 {
  *e=*(S.top-1);
  return OK;
 }
 else
  return ERROR;
}

//针对 [2] 的栈结构
bool GetTop(SqStack * s, ElemType &e){
    if (s->top = -1) return false;  //栈为空，即栈下溢出
    e = s->data[s->top];   //取栈顶元素
    return true
}

清空顺序栈

//针对 [1] 的栈结构，来自 [3]
void ClearStack(SqStack *S)
{ /* 把S置为空栈 */
 (*S).top=(*S).base;
}

顺序栈的长度

//针对 [1] 的栈结构，来自 [3]
int StackLength(SqStack S)
{ /* 返回S的元素个数，即栈的长度 */
 return S.top-S.base;
}

依次访问顺序栈所有元素

//针对 [1] 的栈结构，来自 [3]
void StackTraverse(SqStack S, void(*visit)(SElemType))
{ /* 从栈底到栈顶依次对栈中每个元素调用函数visit() */
 while(S.top > S.base)
  visit(*S.base++);
 printf("\n");
}

链栈的存储结构

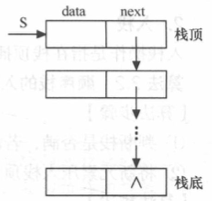
1. 参考资料 [1] 中关于链栈的定义：

   //链栈的存储结构
   typedef struct StackNode{
       ElemType data;
       struct StackNode *next;
   }StackNode, *LinkStack;
   

   • 以链表的头部作为栈顶

   • 不附加头结点

     

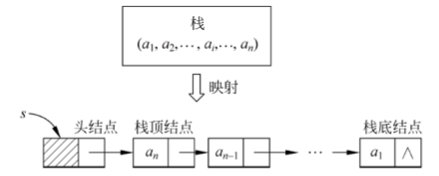
2. 参考资料 [2] 中关于链栈的定义：

   typedef struct linknode{
       ElemType data;   //数据域
       struct linknode * next;   //指针域
   }LinkStNode;
   

   • 采用带头结点的单链表实现链栈。

     

   • 链栈的优点：不存在栈满上溢出情况。

   • 规定所有操作都在单链表的表头进行。首结点是栈顶结点，尾结点是栈底结点。

   • 栈空的条件：s->next == NULL

   • 栈满的条件：由于只有内存溢出时才出现栈满，通过长不考虑此情况，所以在链栈中可以看成不存在栈满

   • 元素 e 进栈操作：新建一个结点存放元素 e （由 p 指向它），将结点 p 插入到头结点之后

   • 出栈操作：取出首结点的 data 值并将其删除。

链栈的基本操作

链栈的初始化

//参考资料 [1] 的算法3.5
Status InitStack(LinkStack &S){//构造一个空栈 S，栈顶指针为置空
    S = NULL;
    return OK;
}

//参考资料 [2]
void InitStack(LinkStNode * &s){
    s = (LinkStNode *)malloc(sizeof(LinkStNode));
    s->next = NULL;
}

时间复杂度：

链栈的入栈

//参考资料 [1] 的算法3.6
//此处的单链表不带头结点
Status Push(LinkStack &S, SElemType e){//在栈顶插入元素 e
    p = new StackNode;  //生成新结点
    p->data = e;   // 将新结点数据域置为 e
    p->next = S;  //将新结点插入栈顶
    S = p;  //修改栈顶指针为 p
    return OK;
}

//参考资料 [2]
//注意，在这里用带头结点的单链表
vodi Push(LinkStNode * &s, ElemType e){
    LinkStNode *p;
    p = (LinkStNode *)malloc(sizeof(LinkStNode));  //新建节点 p
    p->data = e;  //存放元素 e
    p->next = s->next; //将 p 结点插入作为首元结点
    s->next = p; 
}

时间复杂度：

链栈的出栈

//参考资料 [1] 的算法3.7
Status Pop(LinkStack &S, SElemType &e){//删除 S 的栈顶元素，用 e 返回其值
    if (S == NULL) return ERROR;  //栈空
    e = S->data;  //将栈顶元素赋给 e
    p = S;   //用 p 临时保存栈顶元素空间，以备释放
    S = S->next;    //修改栈顶指针
    delete p;    //释放原栈顶元素空间
    return OK;
}

//参考资料 [2]
bool Pop(LinkStNode * &s, ElemType &e){
    LinkStNode * p;
    if(s->next == NULL) return false;  //栈空的情况
    p = s->next;  // p 指向首元结点
    e = p->data;  //提取首元结点的值
    s->next = p->next;  //删除首元结点
    free(p);   //释放被删除的结点存储空间
    return true;
}

时间复杂度：

取链栈的栈顶元素

//参考资料 [1] 的算法3.8
SElemType GetTop(LinkStack S){//返回 S 的栈顶元素，不修改栈顶指针
    if (S != NULL){//栈非空
        return S->data;  //返回栈顶元素的值，栈顶指针不变
    }
}

//参考资料 [2]
bool GetTop(LinkStNode * s, ElemType &e){
    if(s->next != NULL) return false;  //栈空
    e = s->next->data;
    return true;
}

时间复杂度：

销毁链栈

//参考资料 [2]
void DestroyStack(LinkStNode * &s){
    LinkStNode *pre = s, *p = s->next; //pre指向头结点，p指向首元结点
    while(p != NULL){
        free(pre); //释放 pre 结点
        pre = p;
        p = pre->next;  //pre,p同步后移
    }
    free(pre);  //此时 pre 指向尾结点，释放其空间
}

时间复杂度：

判断链栈是否为空

//参考资料 [2]
bool StackEmpty(LinkStNode * s){
    return (s->next == NULL);
}

与判断单链表是否为空的方法一样。

//参考资料 [3] ，不带头结点的单链表
Status ListEmpty(LinkList L)
{ /* 初始条件：线性表L已存在。操作结果：若L为空表，则返回TRUE，否则返回FALSE */
 if(L)
  return FALSE;
 else
  return TRUE;
}

参考资料

[1]. 严蔚敏等. 数据结构：C语言版[M]. 北京：人民邮电出版社，2015.

[2]. 李春葆. 数据结构教程. 北京：清华大学出版社，2017.

[3]. 维基百科：栈[EB/OL]. https://zh.wikipedia.org/wiki/%E5%A0%86%E6%A0%88 , 2023.2.2