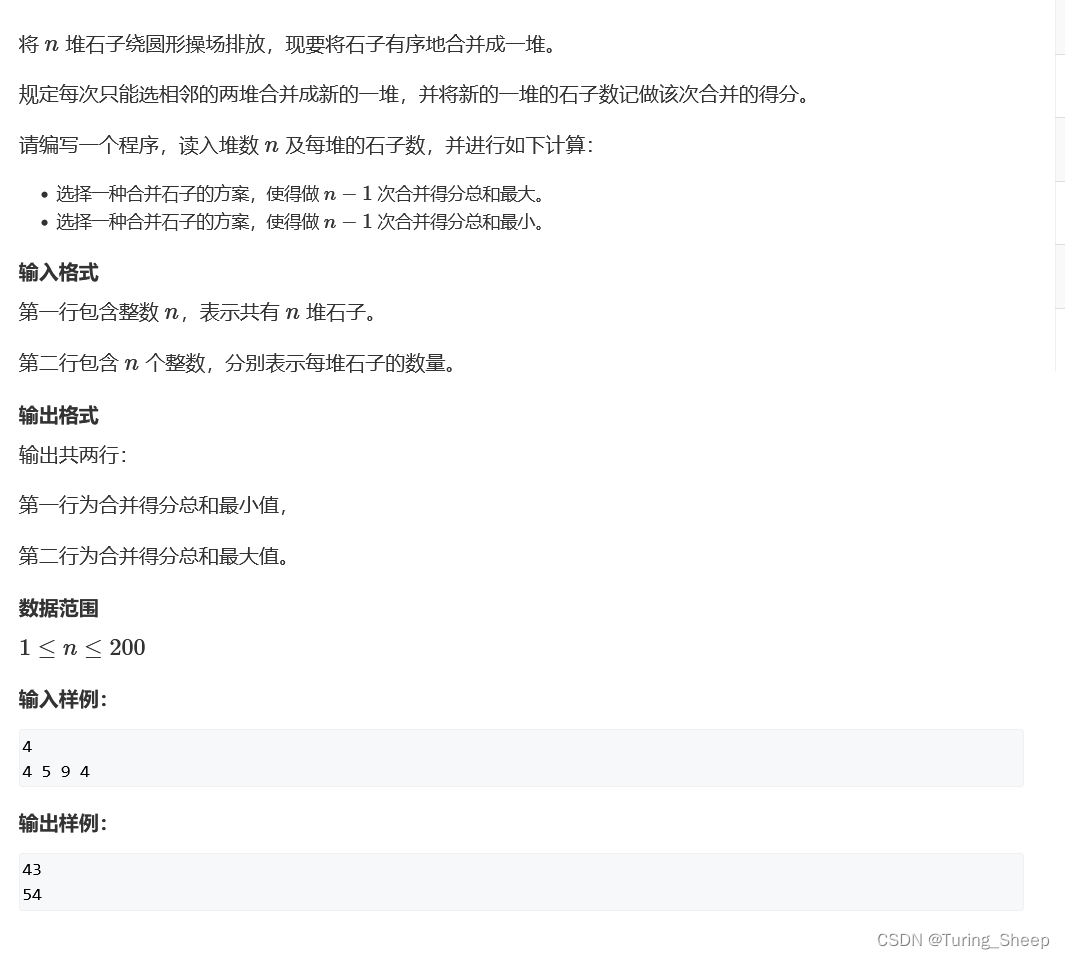
一、问题

二、思路

在讲解这道题之前，我们需要先掌握线性的区间DP问题，如果对于线性区间DP的解决方式还不了解的话，建议先看一下这篇文章：石子合并（区间DP）

那么在了解了线性石子合并问题后，我们现在只剩下了一个难点：如何将环形转化为线性。

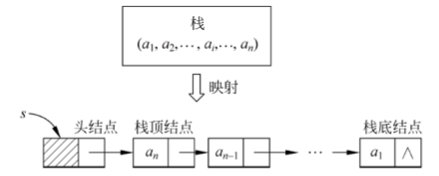
我们看下面图：

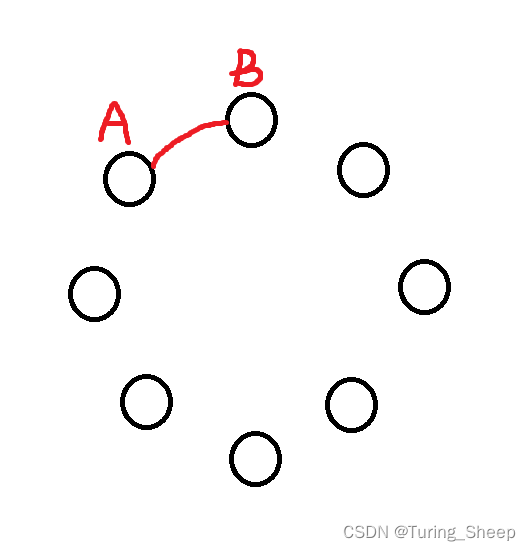
如果我们想要合并A和B的话，我们就在两堆石子之前连接一条线，那么当我们将这一圈石子合并为1堆的时候，情况如下图所示：

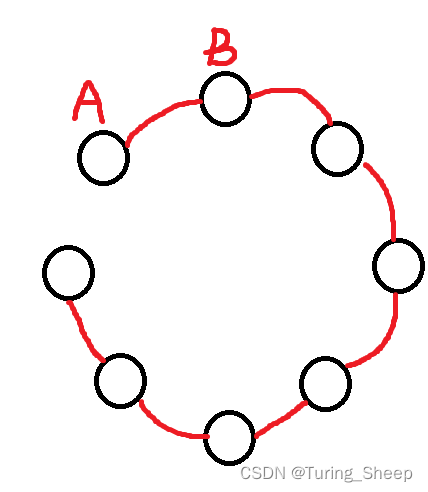
而这恰好就相当于一个线性的石子围成了一个圈，只不过我们的合并方式不同，最终剩下的缺口也不同。

那么我们就可以去枚举每一个缺口，展开为线性，最终在这么多种情况中选出一个最大的。

但是我们发现，我们的缺口有n个，那么这就说明，我们要在之前的区间DP的时间复杂度上再乘上一个n。

很显然这样的做法是不太高效的。

那么怎么办呢？

我们接着看下面这个图：

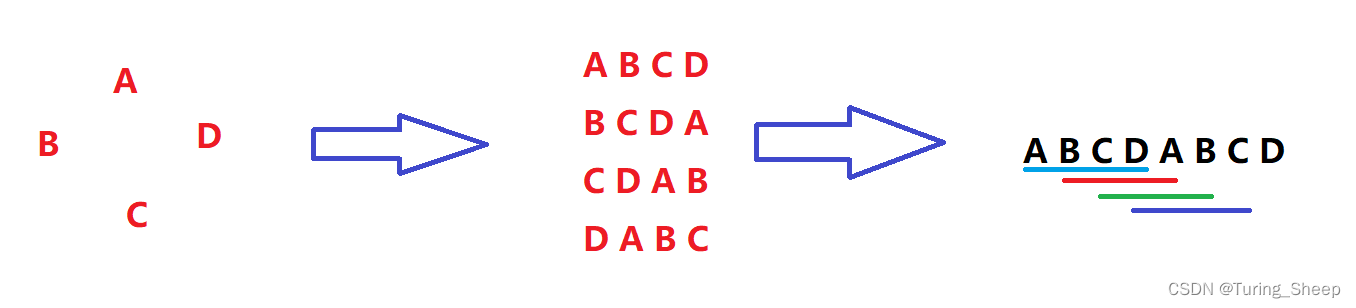
我们发现我们把这个字符串写两遍，这样我们就能在这个2n长度的石子中找到我们枚举的情况。

那么我们就在这个2n长度的石子中进行合并。

按照我们之前区间DP的状态定义，我们令$f[l][r]$表示将区间l到r内的石子合并为1堆所需要的最小值。

我们只需要去枚举所有的长度为n的f[l][r]，然后取出一个最大值。

三、代码

我们在求最小值的时候需要注意初始化为正无穷的问题。

#include<bits/stdc++.h>
using namespace std;
const int N = 510;
const int INF = 0x3f3f3f3f;
int a[N], f[N][N], g[N][N];
int n;
int main()
{
	cin >> n;
	for(int i = 1; i <= n; i ++ )
	{
		cin >> a[i];
		a[i + n] = a[i];
	}
	
	for(int i = 1; i <= 2 * n; i ++ )
	{
		a[i] = a[i - 1] + a[i];
	}

	for(int  len = 2; len <= n; len ++ )
	{
		for(int l = 1; l + len - 1 <= 2 * n; l ++ )
		{
			int r = l + len -1;
			g[l][r] = INF;
			for(int k = l; k < r; k ++ )
			{
				f[l][r] = max(f[l][r], f[l][k] + f[k + 1][r] + a[r] - a[l - 1]);
				g[l][r] = min(g[l][r], g[l][k] + g[k + 1][r] + a[r] - a[l - 1]);
			}
		}
	}
	int maxv = -INF, minv = INF;
	for(int l = 1; l + n - 1 <= 2 * n; l ++ )
	{
		int r = l + n - 1;
		if(maxv < f[l][r])maxv = f[l][r];
		if(minv > g[l][r])minv = g[l][r];
	} 
	cout << minv << endl << maxv << endl;

}