最近突然被问到这个问题，于是复习一下，用最通俗的语言解释。

图

无向图：如下左图各个顶点之间用不带箭头的边连接的图；相应的右图就是有向图

               

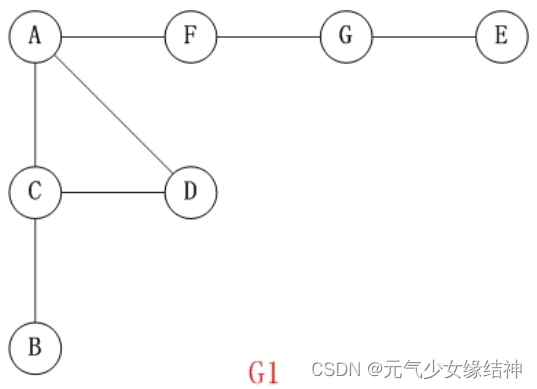
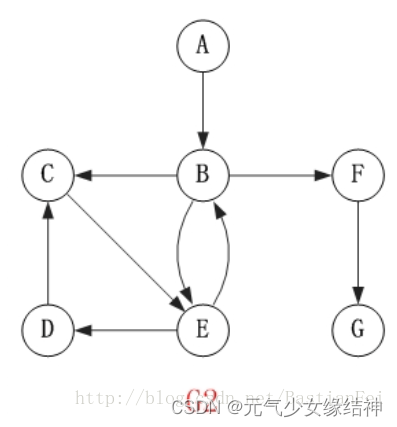
 邻接矩阵

可以理解为表示上述图中顶点与顶点之间是否有直接相连的边（有则是1，无则是0），描述这种关系的二维数组。如下两幅图中的二维矩阵：

 

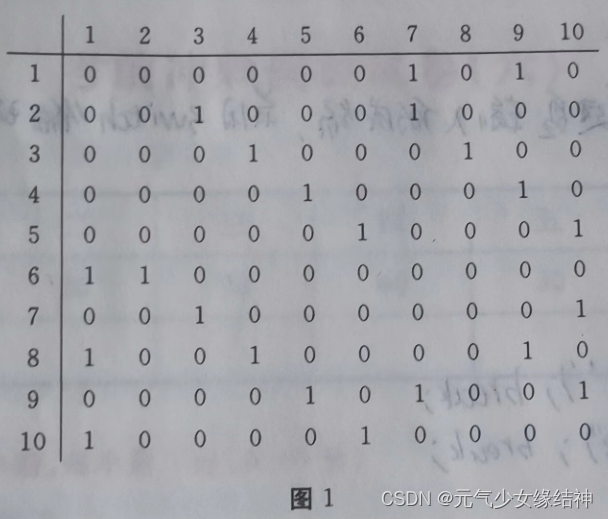
 易知，每个图都可以用对应的邻接矩阵表示出来。其中图1邻接矩阵是非对称的，图2中的邻接矩阵却是对称的（沿主对角线）。

 广度搜索优先遍历

无论广度/深度搜索，均遵循原则：按顺序入队且先入的先出，直到所有的顶点均出完就结束搜索。

结合例子我们先说广度搜索，我理解为同级别的顶点按顺序先遍历完再搜索下一级别的顶点，这样一级一级往下，直到底。

如上面的图G1，以A为顶点广度搜索：

深度搜索优先遍历

 深度搜索优先我理解为一颗倒拔过来的杨柳树，一根枝条摸完摸到底再摸下一根枝条。为了好理解可以每次只入队1个顶点，当一根枝条达到底部时就返回上一级（上上一级、上上上级.......）看是否有为入队过的枝条。如上图的G1以A为顶点深度搜索优先就应该是：

由上面两幅图，很容易理解广度与深度优先，那么G2图的广度、深度优先也容易，即如下：

   

即广度顺序是A->B->C->E->F->D->G 而深度顺序是A->B->C->E->D->F->G 

那么对于图4这种不是图而是用邻接矩阵表示顶点间关系的我们该怎么搜索呢？其实是一样道理，如图4的广度搜索应如下：

即D答案错了一个顺序。继续看另几个答案A应该是0243165，所以A也不正确，即绿框所示0423165即答案C正确。

生成树

理解了上面说的广度、深度优先，我们可以像上面一样计算得到相应的搜索顺序，然后我们根据顺序去画广度优先生成树、深度优先生成树。以图4中的邻接矩阵为例，广度优先搜索生成树就是如下所示，入队的顶点是出队的顶点的下一级，用边连接即可画出：

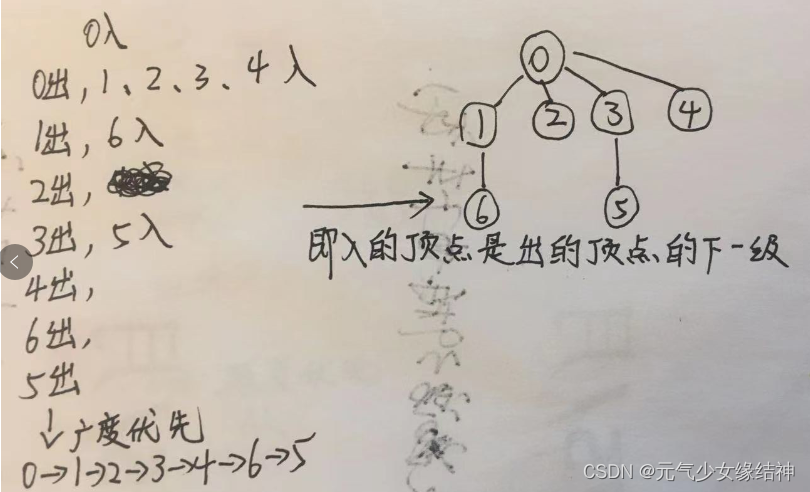
 我们再看图3，图3是不对称的邻接矩阵，意味着有的点是单向连接、有的是双向，而且看得出这个邻接矩阵顶点很多，画图反而有点乱，我们不必画图结构，而是直接跟图4一样使用邻接矩阵直接得到顺序与生成树。

参考：

数据结构——无向图创建邻接表以及深度遍历、广度遍历（C语言版）_正弦定理的博客-CSDN博客_无向图的邻接表的广度遍历

数据结构—无向图创建邻接矩阵、深度优先遍历和广度优先遍历（C语言版）_正弦定理的博客-CSDN博客_邻接矩阵广度优先遍历c语言