当一个有经验的老农看一个瓜是不是好瓜时，他可能会先看下瓜的颜色，一看是青绿的，心想有可能是好瓜；接着他又看了下根蒂，发现是蜷缩着的，老农微微点头，寻思着五成以上是好瓜；最后他又敲了下瓜，一听发出浑浊的响声，基本确定这个瓜是个好瓜！

决策树便是模拟“老农判瓜”的过程，通过对属性的层层筛选从而得到当前样本的分类。

可是，问题在于，老农判瓜依据的是其多年判瓜经验，计算机如何获得这些“识瓜经验”呢？又如何知道哪些属性是更为重要的属性呢？这便是实现决策树需要解决的重要问题。

信息熵

信息熵是度量样本集合纯度最常用的一种指标，信息熵 $Ent(D)$ 的值越小，则样本 $D$ 的纯度越高【即越有序，比如 $D$ 中全是好瓜，则其信息熵就会很小】

信息增益

假定离散属性 $a$ 有$V$个可能的取值 { a 1 , a 2 , . . , a V } \{a^1,a^2,..,a^V\} {a1,a2,..,aV} 【如色泽可以为青绿，乌黑，浅白】，若使用 $a$ 来对样本集合 $D$ 进行划分，则会产生 $V$ 个分支结点【如色泽会分为三部分】，其中第 $v$ 个分支节点包含了 $D$ 中所有在属性 $a$ 上取值为 $a^v$ 的样本，记为 $D^v$ 【如色泽乌黑的样本】。

我们可以根接新的样本集计算出新的信息熵【注意：信息熵的 $k$ 对应的是分类，即好瓜与坏瓜】，再考虑到不同的分支结点所包含样本数不同，给分支结点赋予权重 $\frac{|D^v|}{|D|}$ 【如色泽乌黑的瓜在所有瓜中的比重】，即样本数越多的分支节点造成的影响越大。

由此可以计算出用属性 $a$ 对样本集 $D$ 进行划分所获得的信息增益

$$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)$$

一般而言，信息增益越大，则意味着使用属性 $a$ 来进行划分所获得的纯度提升越大，因此我们可以使用信息增益来进行决策树的划分属性选择，著名的 $ID3$ 算法就是以信息增益为准则来选择划分属性

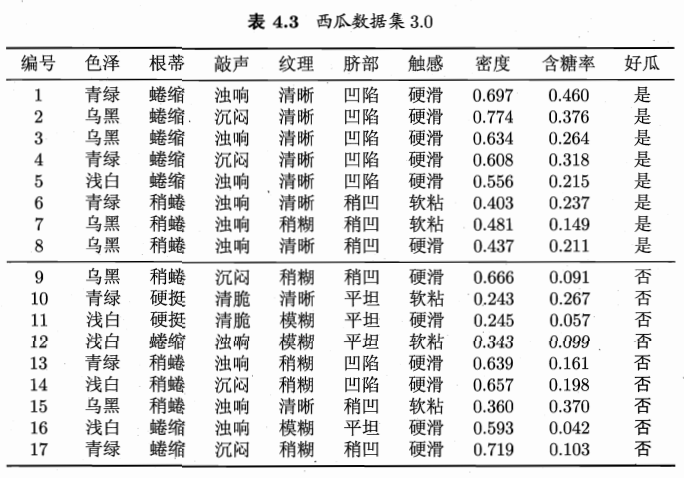
西瓜书 $P75$ 页中通过信息增益选择了纹理作为第一个节点【西瓜书电子版百度云如下👇】

链接：https://pan.baidu.com/s/106WHjk_E5WhmCxTqPj67ng 提取码：zhia

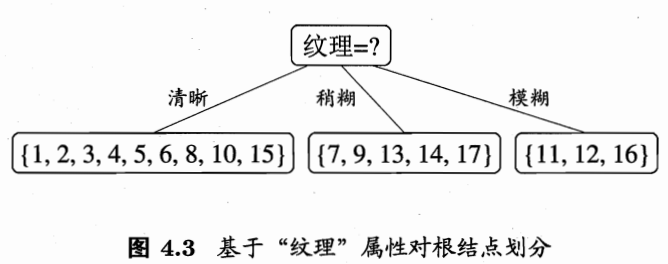
在选择了纹理属性后，接下来在纹理清晰这一分支中应该选择哪一属性继续划分，即计算各个属性在此分支的信息增益，此处以色泽属性为例，演示如何得到西瓜书 $P77$ 的 $Gain(D^1,色泽)=0.043$，为避免上标下标混淆，下边 $D_1$ 代表纹理为清晰的样本集，$D^v$ 代表在纹理清晰的情况下，色泽属性为 $v$ 的样本集

增益率

实际上，信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，，著名的 $C4.5$ 决策树算法不直接使用信息增益，而是使用信息增益率

$$\begin{gathered} Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)} \\ IV(a)=-\sum _{v=1}^V\frac{|D^v|}{|D|}lo{g}_2\frac{|D^v|}{|D|} \end{gathered}$$

以选择根节点为例，计算属性色泽的信息增益率

需要注意的是，增益率准则对可取值数目较少的属性有所偏好，因此 $C4.5$ 算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择信息增益率最高的。

基尼指数

$CART$ 决策树【二叉树形式，如对色泽只有两个属性，青绿，非青绿】使用基尼指数来选择划分属性，数据集 $D$ 的纯度可用基尼值来度量。

基尼值反映了从数据集中随机抽取两个样本，其类别标记不一致的概率【即预测错误的概率】，因此基尼值越小，数据集 $D$ 的纯度越高

由此我们可以得到基尼指数的定义

我们再次使用色泽属性进行举例，计算此时的基尼指数

剪枝

剪枝是决策树学习算法对付“过拟合”的主要手段。在决策树学习中，为了尽可能正确分类训练样本，结点划分过程将不断重复，有时会造成决策树分支过多，这时就可能因训练样本学得“太好”了，以致于把训练集自身得一些特点当成所有数据都具有得一般兴致而导致过拟合。因此，可通过主动去掉一些分支来降低过拟合得风险。

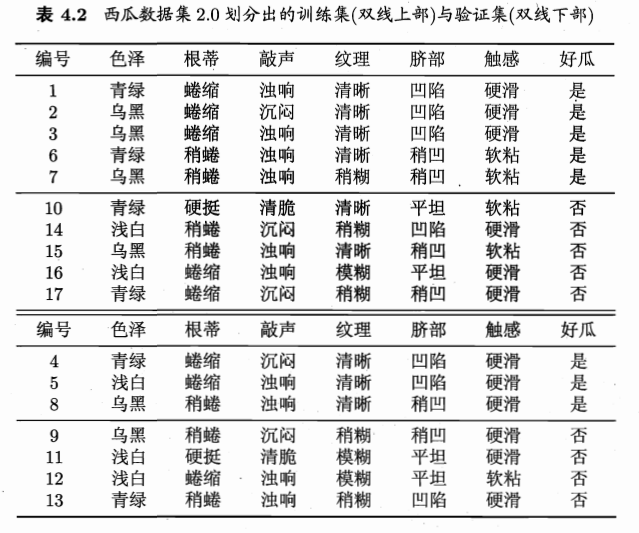
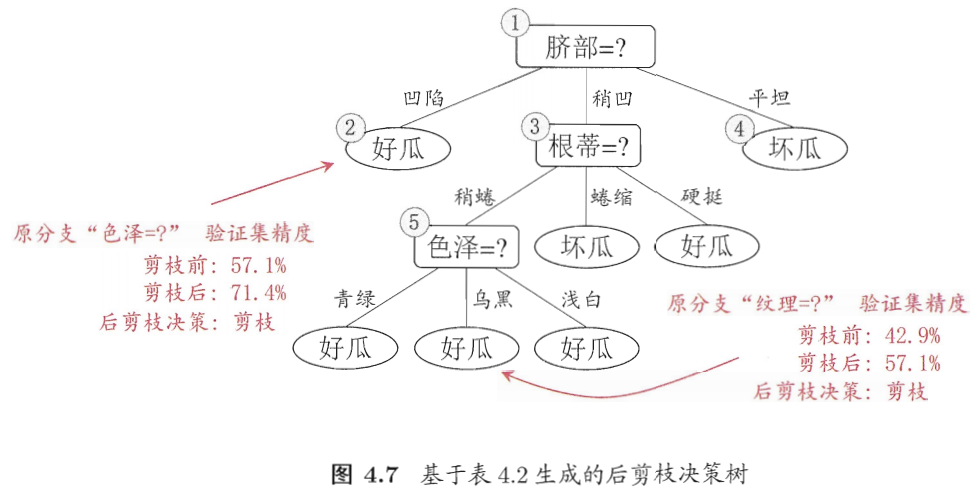
根据信息增益准则生成的决策树

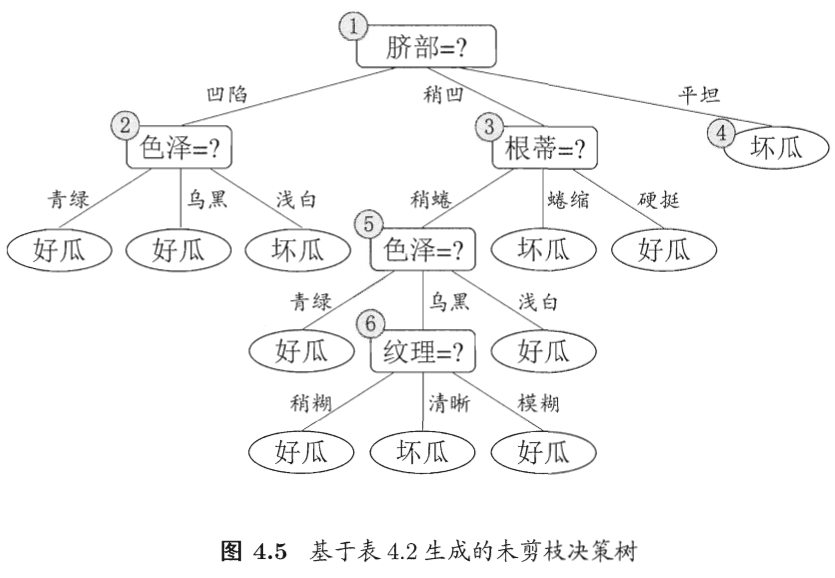
预剪枝

预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点得划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点

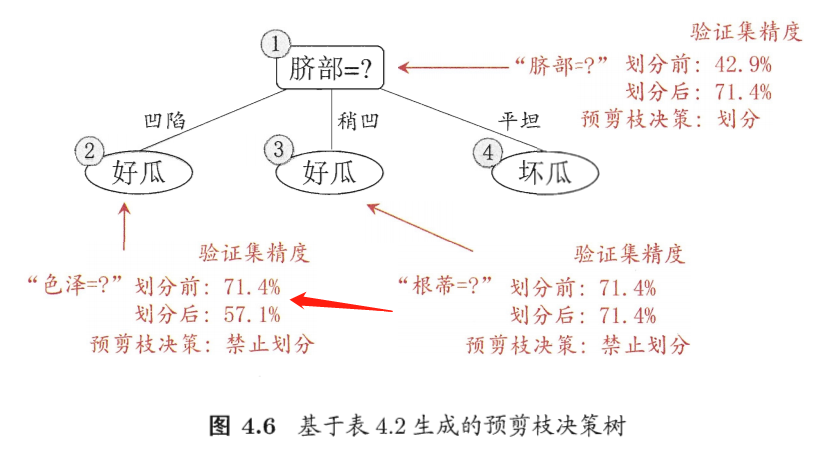
西瓜书中对于脐部的计算已有详细步骤，因此不多赘述。此处对色泽属性是否需要划分进行计算，即计算划分前与划分后的验证集精度【测试集中预测正确的占比】

后剪枝

后剪枝则是先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶子结点

计算方法与预剪枝类似，西瓜书上也有详细步骤，不做过多赘述

剪枝总结

• 预剪枝和后剪枝唯一的区别就是前者在决策树生成过程中决定是否剪枝，后者在决策树构造完成后再次遍历各属性结点决定是否剪枝
• 一般情形下，后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝决策树。但后剪枝过程是在生成完全决策树之后进行的，并且要自底向上地对树中的所有非叶结点进行逐一考察，因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多
• 预剪枝和后剪枝的算法有多种，这里只是展示了最简单的两种，不过基本思想都是一致的，即通过对比剪枝前后的某个指标来决定是否进行剪枝

连续值

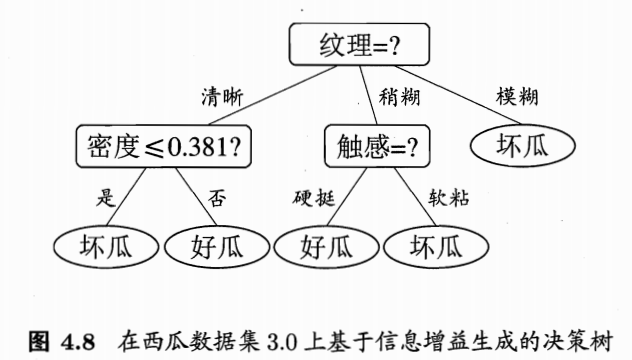
由于连续属性的可取值数目不再有限，因此，不能直接根据连续属性的可取值来对结点进行划分。此时，连续属性离散化技术可派上用场。最简单的策略是采用二分法对连续属性进行处理，这正是 $C4.5$ 决策树算法中采用的机制

比如我们现在相对密度属性进行划分，则操作如下

接着以密度划分点 $0.381$ 为例计算其对应的信息增益

假设在密度所有划分点中，$0.381$ 对应的信息增益最大，则此信息增益就当作密度属性的信息增益，代表密度属性在决策树构建中参与竞选【$密度\le 0.381$ 为坏瓜是因为在训练集中坏瓜占比大 】

缺失值

现实任务中常会遇到不完整样本，即样本的某些属性值缺失。若将有缺失值的样本全部丢弃，显然是对数据集的浪费，因此，使用有缺失值的训练样例来进行学习十分必要

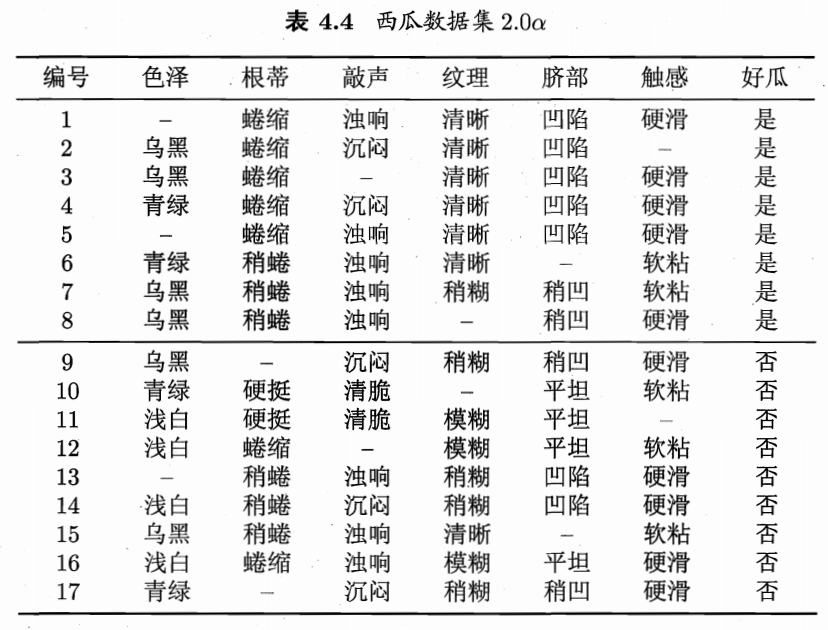
此时信息增益公式再次进行修改

由此可以计算出不同属性对应的信息增益，选择对应的属性结点构造决策树，西瓜书中有构造的详细步骤，此处不再赘述

多变量决策树

若我们把每个属性视为坐标空间中的一个坐标轴，则d个属性描述的样本就对应了 $d$ 维空间中的一个数据点；对样本分类则意味着在这个坐标空间中寻找不同类样本之间的分类边界。决策树所形成的分类边界有一个明显的特点：轴平行，即它的分类边界由若干个与坐标轴平行的分段组成。

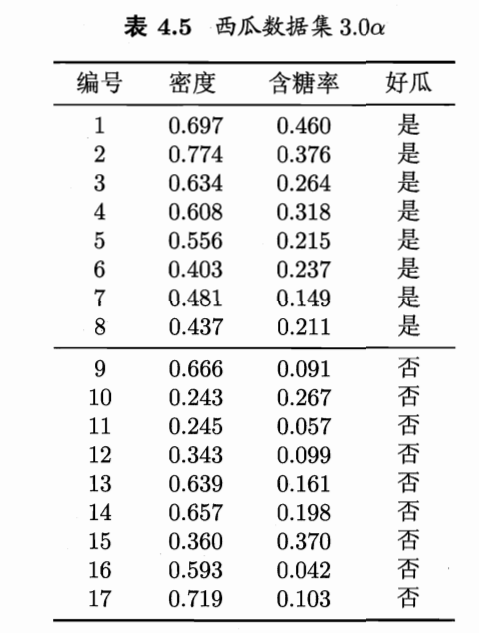
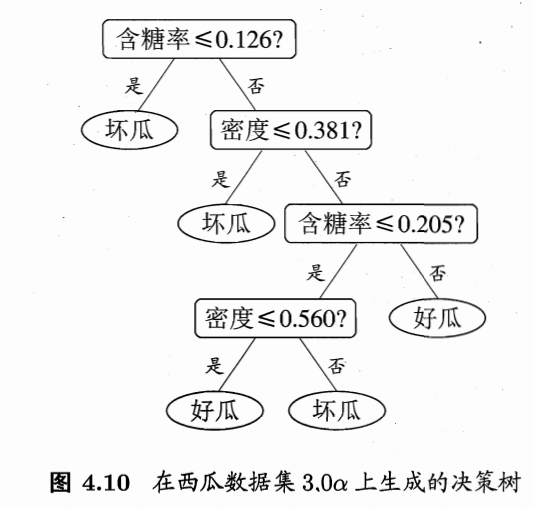
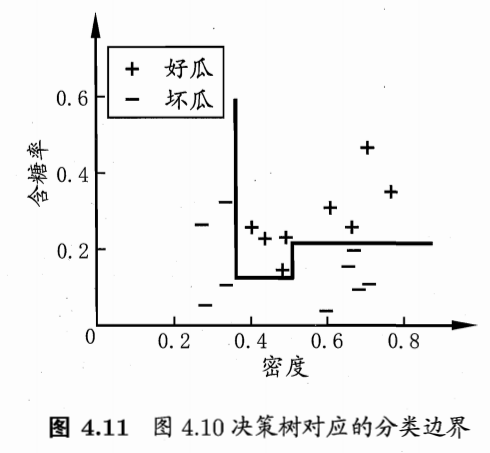
若能使用斜的划分边界，则决策树模型将大为简化。多变量决策树就是能实现这样的“斜划分”甚至更复杂划分的决策树。

以实现斜划分的多变量决策树为例，在此类决策树中,非叶结点不再是仅对某个属性,而是对属性的线性组合进行测试；换言之,每个非叶结点是一个形如 ${\sum }_{i=1}^d{w}_i{a}_i=t$ 的线性分类器，其中 $w_i$ 是属性 $a_i$ 的权重，$w_i$ 和 $t$ 可在该结点所含的样本集和属性集上学得。于是，与传统的单变量决策树不同,在多变量决策树的学习过程中，不是为每个非叶结点寻找一个最优划分属性，而是试图建立一个合适的线性分类器，如下👇

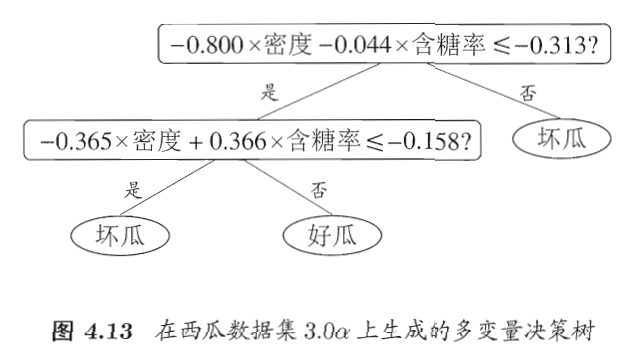
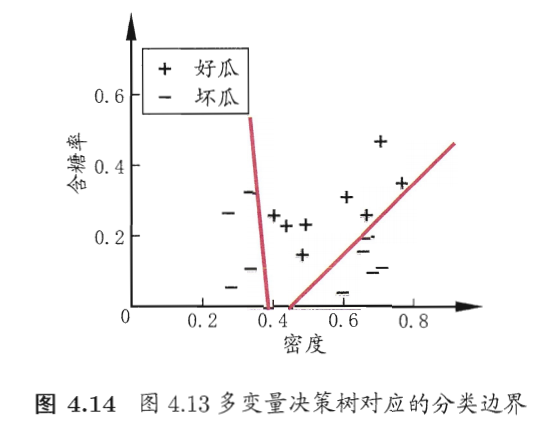
此处仅仅是使用简单例子让我们能够更好理解多变量决策树的意思，并不细究这两条边界是如何得到的。