目录
- 一、简要介绍
- 二、环境设置
- 2.1 实验配置
- 2.2 必要库安装
- 三、数据集解析
- 3.1 数据集加载
- 3.2 数据文件夹结构
- 3.3 点云数据可视化
- 3.4 数据获取与预处理
- 3.5 数据集定义
- 四、模型组网
- 4.1 PointNet 介绍
- 4.2 Paddle模型组网
- 4.3 模型概要
- 五、模型训练
- 六、模型预测
- 七、总结
Hi,大家好,我是半亩花海。 本项目从点云数据的分析出发,利用 Paddle 框架和 PointNet 网络,实现从数据集构建、模型组网到训练、预测全流程开发,实现对飞机零件的点云数据的三维点云分割任务。
一、简要介绍
点云是一种不同于图片的数据存储结构,其特有的无序性,使其在利用深度网络处理时,需要进行特殊的处理。常见的处理方法有将点云处理成体素后,以某种方式将体素转换为图片后进行处理,但这种方法往往伴随着计算量大等缺点。PointNet 模型能够有效处理点云分类、零件分割和语义解析等任务,展示了在处理非结构化数据时的优越性和灵活性。点云分割是根据空间、几何和纹理等特征对点云进行划分,使得同一划分内的点云拥有相似的特征。
二、环境设置
2.1 实验配置
由于深度学习对 GPU 要求较高,本文采用高配置的 “AutoDL 算力云” 云服务器,使用 PaddlePaddle 2.4.0 作为深度学习框架进行飞机零件的3D点云分割,实验配置如下表所示。
| 项目 | 参数 |
|---|---|
| GPU | RTX 4090D(24GB) * 1 |
| CPU | 16 vCPU Intel® Xeon® Platinum 8481C |
| 显存 | 80GB |
| 硬盘 | 系统盘:30 GB;数据盘:50GB(免费) |
| 操作系统 | Ubuntu 18.04 |
| 开发语言 | Python 3.8 |
| 深度学习框架 | PaddlePaddle 2.4.0 |
| CUDA | 11.2 |
2.2 必要库安装
import os
import tqdm
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore", module="matplotlib") # 忽略matplotlib的警告
from mpl_toolkits.mplot3d import Axes3D # 导入3D绘图工具包
# 导入Paddle相关库
import paddle
from paddle.io import Dataset
import paddle.nn.functional as F
from paddle.nn import Conv2D, MaxPool2D, Linear, BatchNorm, Dropout, ReLU, Softmax, Sequential
# 查看Paddle版本
print('本项目使用paddle版本:{}'.format(paddle.__version__))

三、数据集解析
3.1 数据集加载
ShapeNet 数据集是一项持续的工作,旨在建立一个带有丰富注释的大规模 3D 形状数据集。形状网核心是完整形状网数据集的子集,具有干净的单个 3D 模型和手动验证的类别和对齐注释。它涵盖了 55 个常见的对象类别,约有 51,300 个独特的 3D 模型。
对于此示例,我们使用 PASCAL 3D+ 的 12 个对象类别之一,以飞机零件的分割为例,该类别作为 ShapenetCore 数据集的一部分包含在内。完整的数据集下载地址:https://shapenet.cs.stanford.edu/iccv17/ 。
3.2 数据文件夹结构
构建该数据集,PointNet 文件夹的结构如下:
PointNet/
├── dataset/
│ ├── shapenet/
│ ├── train_data/
│ ├── Airplane/
│ ├── 000043.pts(example)
│ ├── train_label/
│ ├── Airplane/
│ ├── 000043.seg(example)
├── output/
│ ├── PointNet_{}.pdparams
│ └── PointNet_{}.pdopt
└── 21142604.ipynb
3.3 点云数据可视化
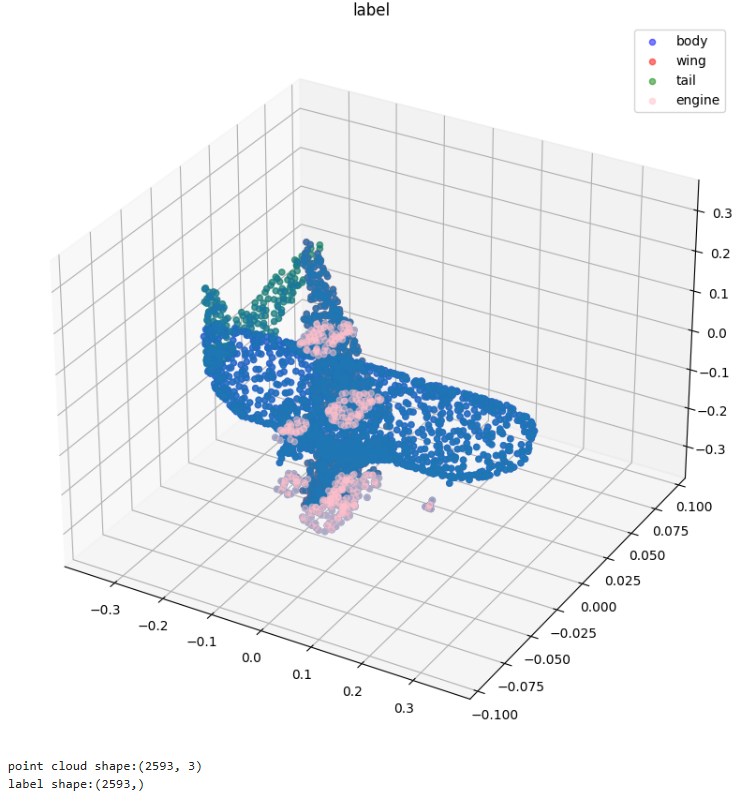
点云数据的获取方式,一般都是使用深度相机或者雷达,其存储的形式一般为一个(N,4)的向量,其中,N 代表着这次采集的点云数量,4 代表着其中每个点在三维的坐标 x,y,z 和反射强度 r,但在本次的数据集中,点云的存储方式为(N,3),即不包括点云的反射强度 r。而 label 的存储方式则是为一个N维的向量,代表每个点具体的类别。
下面,我们通过读取点云的数据 data 和其标签 label,对我们需要处理的数据,有一个大致的认识。
# 可视化使用的颜色和对应label的名字
COLORS = [' ', 'b', 'r', 'g', 'pink']
label_map = ['', 'body', 'wing', 'tail', 'engine']
# 定义可视化函数
def visualize_data(point_cloud, label, title):
# 创建数据框架用于存储点云数据和对应的标签
df = pd.DataFrame(
data={
"x": point_cloud[:, 0],
"y": point_cloud[:, 1],
"z": point_cloud[:, 2],
"label": label,
}
)
# 创建3D图形对象
fig = plt.figure(figsize=(15, 10))
ax = plt.axes(projection="3d")
# 散点图绘制所有点云数据
ax.scatter(df["x"], df["y"], df["z"])
# 根据标签绘制不同颜色的点
for i in range(label.min(), label.max() + 1):
c_df = df[df['label'] == i]
ax.scatter(c_df["x"], c_df["y"], c_df["z"], label=label_map[i], alpha=0.5, c=COLORS[i])
ax.legend() # 添加图例
plt.title(title)# 设置图形标题
plt.show()# 显示图形
# 定义点云和标签文件路径
show_point_cloud_path = 'dataset/shapenet/train_data/Airplane/000043.pts'
show_label_path = 'dataset/shapenet/train_label/Airplane/000043.seg'
# 读取点云文件
point_cloud = np.loadtxt(show_point_cloud_path)
label = np.loadtxt(show_label_path).astype('int') # 读取标签文件并转换为整数类型
visualize_data(point_cloud, label, 'label') # 可视化点云数据
# 打印点云和标签的形状
print('point cloud shape:{}'.format(point_cloud.shape))
print('label shape:{}'.format(label.shape))
3.4 数据获取与预处理
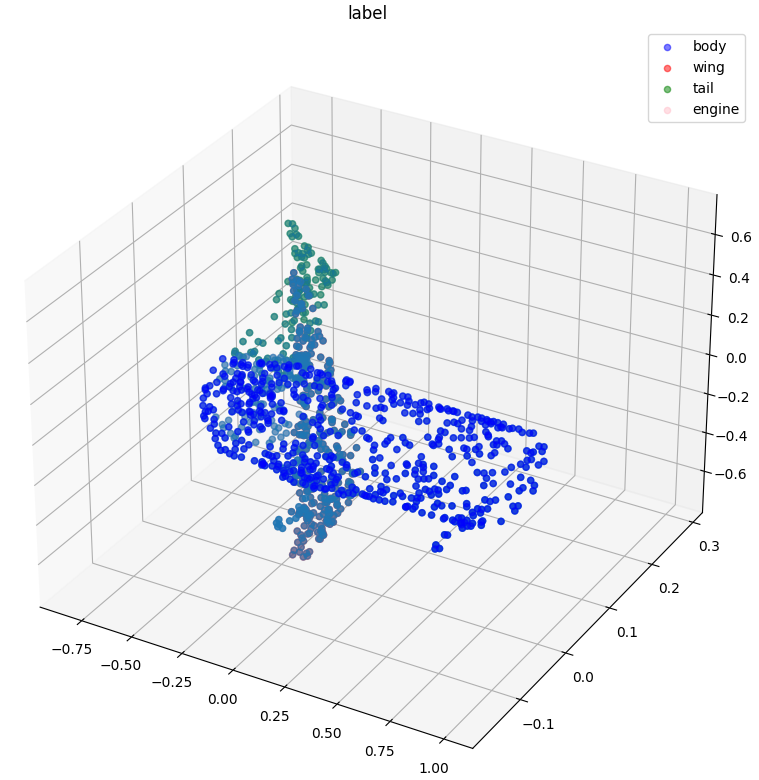
根据上面的可视化分析,我们可以知道,每个数据中点云 N 的数量是不同的,这不利于我们进行后续的处理,所以这里对数据集中的点云进行了随机采样,使每个点云的数量一致,此外,我们也将点云的坐标进行了正则化操作,最后将处理好的点云存储在内存中,方便后续 dataset 的构建。
此数据集中不仅包含 Airplane 类别,还包括 Bag,Cap,Car, Chair 类别,我们可以修改数据集和标签路径(data_path 和 label_path),进而对其他类别数据集进行使用。
# 定义数据和标签路径
data_path = 'dataset/shapenet/train_data/Airplane'
label_path = 'dataset/shapenet/train_label/Airplane'
# 采样点
NUM_SAMPLE_POINTS = 1024
# 存储点云与label
point_clouds = []
point_clouds_labels = []
# 获取数据目录下的所有文件名
file_list = os.listdir(data_path)
for file_name in tqdm.tqdm(file_list):
# 获取label和data的地址
label_name = file_name.replace('.pts', '.seg')
point_cloud_file_path = os.path.join(data_path, file_name)
label_file_path = os.path.join(label_path, label_name)
# 读取label和data
point_cloud = np.loadtxt(point_cloud_file_path)
label = np.loadtxt(label_file_path).astype('int')
# 如果点云数据少于需要采样的点,则直接去除
if len(point_cloud) < NUM_SAMPLE_POINTS:
continue
# 获取点云数据的点数
num_points = len(point_cloud)
# 随机选择采样的索引
sampled_indices = random.sample(list(range(num_points)), NUM_SAMPLE_POINTS)
# 根据采样索引获取采样后的点云数据和标签数据
sampled_point_cloud = np.array([point_cloud[i] for i in sampled_indices])
sampled_label_cloud = np.array([label[i] for i in sampled_indices])
# 正则化处理,去中心化并归一化
norm_point_cloud = sampled_point_cloud - np.mean(sampled_point_cloud, axis=0)
norm_point_cloud /= np.max(np.linalg.norm(norm_point_cloud, axis=1))
# 存储采样后的点云数据和标签数据
point_clouds.append(norm_point_cloud)
point_clouds_labels.append(sampled_label_cloud)

# 可视化第一个采样后的点云数据和标签
visualize_data(point_clouds[0], point_clouds_labels[0], 'label')
3.5 数据集定义
在 Paddle 中,数据集的定义需完成以下四步:
- paddle.io.Dataset 的继承
- 构造函数的实现,主要完成一些初始化
- __gtitem__方法的实现,即定义 index 时,可以返回对应的单条数据,包括训练数据和对应的标签
- __len__方法的实现,即获取数据的大小
此外,这里还对数据集进行了训练集和验证集的划分,划分比例为验证集占总体的 20% ,并将定义好的数据集,通过 paddle.io.DataLoader 进行迭代器的封装,方便训练过程数据的读取操作。
class MyDataset(Dataset):
# 步骤一:继承paddle.io.Dataset类
def __init__(self, data, label):
# 步骤二:实现构造函数,定义数据集大小
super(MyDataset, self).__init__()
self.data = data
self.label = label
def __getitem__(self, index):
# 步骤三:实现__getitem__方法,定义指定index时如何获取数据,并返回单条数据(训练数据,对应的标签)
data = self.data[index]
# 减1是因为原始label中是从1开始算类别数的
label = self.label[index] - 1
# 将数据重塑为(1, 1024, 3)的形状
data = np.reshape(data, (1, 1024, 3))
return data, label
def __len__(self):
# 步骤四:实现__len__方法,返回数据集总数目
return len(self.data)
# 数据集划分
VAL_SPLIT = 0.2
split_index = int(len(point_clouds) * (1 - VAL_SPLIT))
# 划分训练集和验证集
train_point_clouds = point_clouds[:split_index]
train_label_cloud = point_clouds_labels[:split_index]
val_point_clouds = point_clouds[split_index:]
val_label_cloud = point_clouds_labels[split_index:]
# 打印训练集和验证集的大小
print("Num train point clouds:", len(train_point_clouds))
print("Num train point cloud labels:", len(train_label_cloud))
print("Num val point clouds:", len(val_point_clouds))
print("Num val point cloud labels:", len(val_label_cloud))
# 测试定义的数据集
train_dataset = MyDataset(train_point_clouds, train_label_cloud)
val_dataset = MyDataset(val_point_clouds, val_label_cloud)
print('=============custom dataset test=============')
# 测试一个数据点的形状
for data, label in train_dataset:
print('data shape:{} \nlabel shape:{}'.format(data.shape, label.shape))
break
# 定义批处理大小
BATCH_SIZE = 64
# 数据加载器
train_loader = paddle.io.DataLoader(train_dataset, batch_size=BATCH_SIZE, shuffle=True)
val_loader = paddle.io.DataLoader(val_dataset, batch_size=BATCH_SIZE, shuffle=False)

四、模型组网
4.1 PointNet 介绍
1. 点云数据的特点
PointNet 网络的设计主要是解决以下三个问题:
- 点云的无序性: 对称函数(symmetry function)的应用,如加法、乘法和取最大值函数等,在 PointNet 则是采用了 maxpooling(最大值汇聚)的方法。
- 点云的交互性: 在分割网络的分支里,可以看到其将某一层的信息和经过 maxpooling 得到的全局信息进行 concate 来达到全局和局部信息的交互。
- 点云的变换不变性: 在点云中,不论怎么旋转应该都不会改变其属性。在此前有人设计变换矩阵,以数据增强的方法来解决这个问题。而这里直接将这个变换矩阵的学习也融入到网络中,设计了 input transform 结构。
2. PointNet 基本出发点
由于点的无序性,需要模型具有置换不变性。
f ( x 1 , x 2 , … , x n ) ≡ f ( x π 1 , x π 2 , … , x π n ) , x i ∈ R D f\left(x_1, x_2, \ldots, x_n\right) \equiv f\left(x_{\pi_1}, x_{\pi_2}, \ldots, x_{\pi_n}\right), \quad x_i \in \mathbb{R}^D f(x1,x2,…,xn)≡f(xπ1,xπ2,…,xπn),xi∈RD
那么可以使用下列公式来体现:
f ( x 1 , x 2 , … , x n ) = max { x 1 , x 2 , … , x n } f\left(x_1, x_2, \ldots, x_n\right)=\max \left\{x_1, x_2, \ldots, x_n\right\} f(x1,x2,…,xn)=max{x1,x2,…,xn}
f ( x 1 , x 2 , … , x n ) = x 1 + x 2 + … + x n f\left(x_1, x_2, \ldots, x_n\right)=x_1+x_2+\ldots+x_n f(x1,x2,…,xn)=x1+x2+…+xn
求 max 值与位置没有关系,使用加法也是与位置无关。那么我们就直接使用 Max 函数:
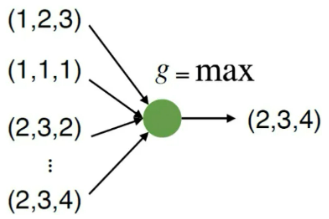
但是这样会导致我们的特征太少,损失太多。那么如何解决?我们可以先升维然后再做 Max 操作(其实就是神经网络的隐层)
f ( x 1 , x 2 , … , x n ) = γ ∘ g ( h ( x 1 ) , … , h ( x n ) ) f\left(x_1, x_2, \ldots, x_n\right)=\gamma \circ g\left(h\left(x_1\right), \ldots, h\left(x_n\right)\right) f(x1,x2,…,xn)=γ∘g(h(x1),…,h(xn))
上面提及到了升维这个东西,神经网络本质就是一个特征提取器,下面的 MLP 可以理解为一个感知机,可以为全连接层、卷积等等,把它上升为一个高维特征,再经过 max 函数得到全局再进行输出。
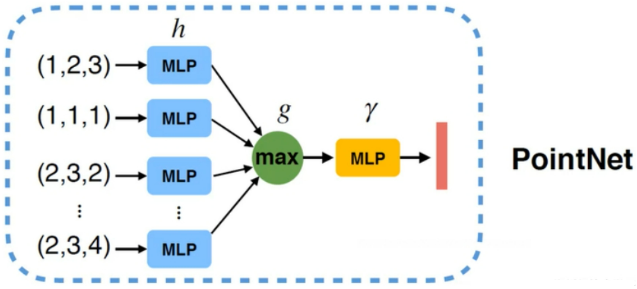
3. PointNet 算法网络架构
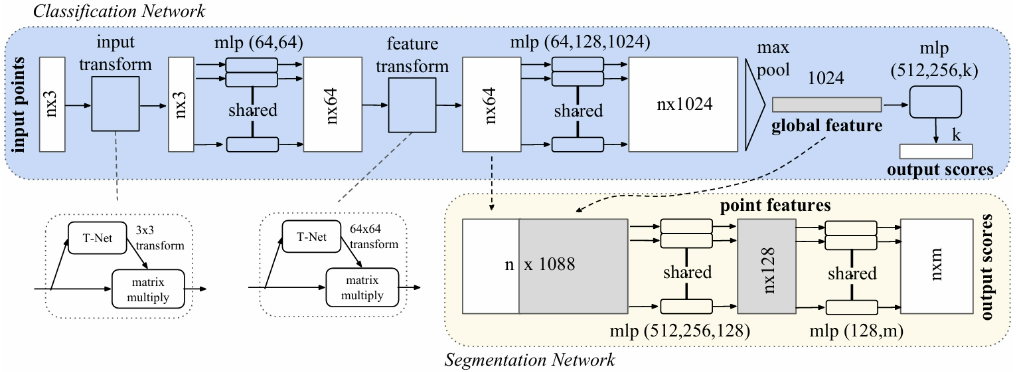
网络有三个关键模块:
- 最大池化层(作为聚合所有点信息的对称函数)
- 局部和全局信息组合结构
- 两个对齐输入点和点特征的联合对齐网络
例如,对于无序输入的对称函数(Symmetry Function for Unordered Input)来说:
为了使模型对输入置换保持不变,我们的方法是通过对点集中的变换元素使用一个对称函数来近似定义点集中的一般函数。
f ( { x 1 , … , x n } ) ≈ g ( h ( x 1 ) , … , h ( x n ) ) f\left(\left\{x_1, \ldots, x_n\right\}\right) \approx g\left(h\left(x_1\right), \ldots, h\left(x_n\right)\right) f({x1,…,xn})≈g(h(x1),…,h(xn))
其中,h 采用多层感知机(MLP),g 采用一个单变量函数和最大池化函数的组合。通过 h 的集合,可以学习许多 f 来捕获集合的不同属性。
4.2 Paddle模型组网
基于 PaddlePaddle 框架组建 PointNet 网络,整个网络包含输入变换网络、MLP、特征变换网络和分割网络等模块。其组网过程与 torch 无大致区别,继承 nn.Layer 后,重写前向传播 forward 方法。
其中代码中的网络定义,对应网络细节如下:
- input_transform_net+input_fc: 对应 T-Net,后续 reshape 到 3x3 做为变换矩阵和输入进行变换。
- mlp: 对应升维的 MLP 层,均使用了 1x1 的卷积层。
- seg_net: 对应 Segmentation Network 中一系列的 MLP 层。
class PointNet(paddle.nn.Layer):
def __init__(self, name_scope='PointNet_', num_classes=4, num_point=1024):
super(PointNet, self).__init__()
self.num_point = num_point
# 输入变换网络
self.input_transform_net = Sequential(
Conv2D(1, 64, (1, 3)),
BatchNorm(64),
ReLU(),
Conv2D(64, 128, (1, 1)),
BatchNorm(128),
ReLU(),
Conv2D(128, 1024, (1, 1)),
BatchNorm(1024),
ReLU(),
MaxPool2D((num_point, 1))
)
# 输入变换的全连接层
self.input_fc = Sequential(
Linear(1024, 512),
ReLU(),
Linear(512, 256),
ReLU(),
Linear(256, 9,
weight_attr=paddle.framework.ParamAttr(initializer=paddle.nn.initializer.Assign(paddle.zeros((256, 9)))),
bias_attr=paddle.framework.ParamAttr(initializer=paddle.nn.initializer.Assign(paddle.reshape(paddle.eye(3), [-1])))
)
)
# MLP 第一部分
self.mlp_1 = Sequential(
Conv2D(1, 64, (1, 3)),
BatchNorm(64),
ReLU(),
Conv2D(64, 64,(1, 1)),
BatchNorm(64),
ReLU(),
)
# 特征变换网络
self.feature_transform_net = Sequential(
Conv2D(64, 64, (1, 1)),
BatchNorm(64),
ReLU(),
Conv2D(64, 128, (1, 1)),
BatchNorm(128),
ReLU(),
Conv2D(128, 1024, (1, 1)),
BatchNorm(1024),
ReLU(),
MaxPool2D((num_point, 1))
)
# 特征变换的全连接层
self.feature_fc = Sequential(
Linear(1024, 512),
ReLU(),
Linear(512, 256),
ReLU(),
Linear(256, 64*64)
)
# MLP 第二部分
self.mlp_2 = Sequential(
Conv2D(64, 64, (1, 1)),
BatchNorm(64),
ReLU(),
Conv2D(64, 128,(1, 1)),
BatchNorm(128),
ReLU(),
Conv2D(128, 1024,(1, 1)),
BatchNorm(1024),
ReLU(),
)
# 最后的分割网络
self.seg_net = Sequential(
Conv2D(1088, 512, (1, 1)),
BatchNorm(512),
ReLU(),
Conv2D(512, 256, (1, 1)),
BatchNorm(256),
ReLU(),
Conv2D(256, 128, (1, 1)),
BatchNorm(128),
ReLU(),
Conv2D(128, 128, (1, 1)),
BatchNorm(128),
ReLU(),
Conv2D(128, num_classes, (1, 1)),
Softmax(axis=1)
)
def forward(self, inputs):
batchsize = inputs.shape[0]
# 输入变换网络前向传播
t_net = self.input_transform_net(inputs)
t_net = paddle.squeeze(t_net)
t_net = self.input_fc(t_net)
t_net = paddle.reshape(t_net, [batchsize, 3, 3])
# 将输入点云数据变换
x = paddle.reshape(inputs, shape=(batchsize, 1024, 3))
x = paddle.matmul(x, t_net)
x = paddle.unsqueeze(x, axis=1)
x = self.mlp_1(x)
# 特征变换网络前向传播
t_net = self.feature_transform_net(x)
t_net = paddle.squeeze(t_net)
t_net = self.feature_fc(t_net)
t_net = paddle.reshape(t_net, [batchsize, 64, 64])
# 将特征数据变换
x = paddle.reshape(x, shape=(batchsize, 64, 1024))
x = paddle.transpose(x, (0, 2, 1))
x = paddle.matmul(x, t_net)
x = paddle.transpose(x, (0, 2, 1))
x = paddle.unsqueeze(x, axis=-1)
point_feat = x
x = self.mlp_2(x)
x = paddle.max(x, axis=2)
# 扩展全局特征并与点特征拼接
global_feat_expand = paddle.tile(paddle.unsqueeze(x, axis=1), [1, self.num_point, 1, 1])
x = paddle.concat([point_feat, global_feat_expand], axis=1)
# 最后的分割网络前向传播
x = self.seg_net(x)
x = paddle.squeeze(x, axis=-1)
x = paddle.transpose(x, (0, 2, 1))
return x
4.3 模型概要
# 创建 PointNet 模型实例
pointnet = PointNet()
# 打印模型摘要信息
paddle.summary(pointnet, (64, 1, 1024, 3)) # 第一个参数是模型实例,第二个参数是输入数据的形状
五、模型训练
模型训练中使用的参数如下:
- 优化器:Adam,其中 weight_decay=0.001
- 损失函数:CrossEntropyLoss
- 训练轮数:epoch_num=100
- 保存轮数:save_interval=2
- 验证轮数:val_interval=2
- 最佳准确率初始化:best_acc = 0
- 模型保存地址:output_dir=’./output’
# 创建模型
model = PointNet()
model.train()
# 优化器定义
optim = paddle.optimizer.Adam(parameters=model.parameters(), weight_decay=0.001)
# 损失函数定义
loss_fn = paddle.nn.CrossEntropyLoss()
# 评价指标定义
m = paddle.metric.Accuracy()
# 参数设定
epoch_num = 100 # 训练轮数
save_interval = 2 # 每多少个epoch保存
val_interval = 2 # 每多少个epoch验证
best_acc = 0 # 最佳准确率初始化
# 模型保存地址
output_dir = './output'
if not os.path.exists(output_dir):
os.makedirs(output_dir)
# 训练过程
plot_acc = []
plot_loss = []
for epoch in range(1, epoch_num + 1): # 从1开始计数,到epoch_num结束
total_loss = 0
for batch_id, data in enumerate(train_loader()):
inputs = paddle.to_tensor(data[0], dtype='float32') # 转换输入数据类型
labels = paddle.to_tensor(data[1], dtype='int64') # 转换标签数据类型
predicts = model(inputs) # 前向传播,获得预测结果
# 计算损失和反向传播
loss = loss_fn(predicts, labels)
total_loss += loss.numpy()[0]
loss.backward()
# 计算acc
predicts = paddle.reshape(predicts, (predicts.shape[0]*predicts.shape[1], -1))
labels = paddle.reshape(labels, (labels.shape[0]*labels.shape[1], 1))
correct = m.compute(predicts, labels)
m.update(correct)
# 优化器更新
optim.step()
optim.clear_grad()
avg_loss = total_loss / (batch_id + 1) # 平均损失
plot_loss.append(avg_loss)
print("epoch: {}/{}, loss is: {}, acc is:{}".format(epoch, epoch_num, avg_loss, m.accumulate()))
m.reset()
# 保存
if epoch % save_interval == 0:
model_name = str(epoch)
paddle.save(model.state_dict(), './output/PointNet_{}.pdparams'.format(model_name))
paddle.save(optim.state_dict(), './output/PointNet_{}.pdopt'.format(model_name))
# 训练中途验证
if epoch % val_interval == 0:
model.eval() # 切换到验证模式
for batch_id, data in enumerate(val_loader()):
inputs = paddle.to_tensor(data[0], dtype='float32') # 转换输入数据类型
labels = paddle.to_tensor(data[1], dtype='int64') # 转换标签数据类型
predicts = model(inputs) # 前向传播,获得预测结果
predicts = paddle.reshape(predicts, (predicts.shape[0] * predicts.shape[1], -1))
labels = paddle.reshape(labels, (labels.shape[0] * labels.shape[1], 1))
correct = m.compute(predicts, labels)
m.update(correct)
val_acc = m.accumulate()
plot_acc.append(val_acc)
if val_acc > best_acc:
best_acc = val_acc
print("===================================val===========================================")
print('val best epoch in:{}, best acc:{}'.format(epoch, best_acc))
print("===================================train===========================================")
# 保存最佳模型
paddle.save(model.state_dict(), './output/best_model.pdparams')
paddle.save(optim.state_dict(), './output/best_model.pdopt')
m.reset()
model.train() # 切换回训练模式
将训练结果可视化,如下代码所示。
# 可视化模型训练过程
def plot_result(item, title):
plt.figure()
plt.xlabel("Epochs")
plt.plot(item)
plt.title(title, fontsize=14)
plt.grid()
plt.show()
# 绘制验证集准确率变化图和训练损失变化图
plot_result(plot_acc, 'val acc')
plot_result(plot_loss, 'training loss')
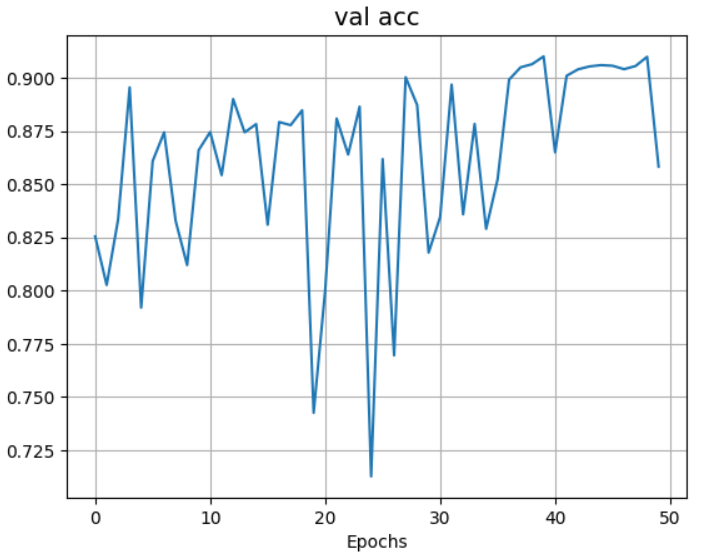
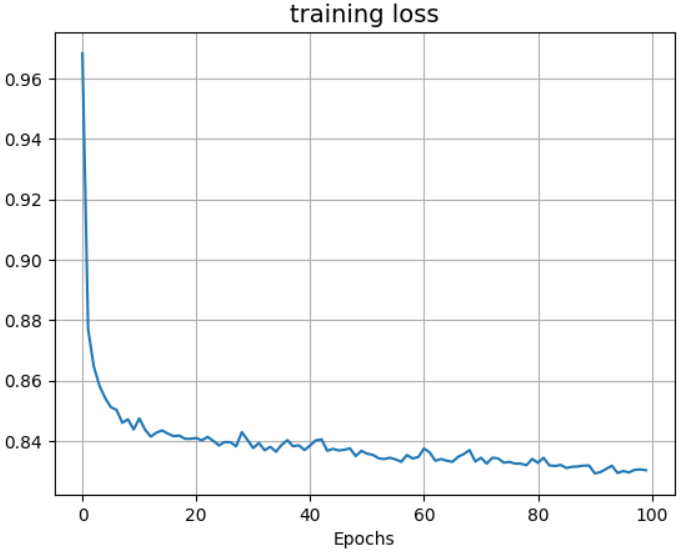
由上述结果可知,验证集准确率稳定在 80%-90% ,最高达到 91.45%,而训练集损失率随着训练世代的增加而越来越低,说明本实验中 PointNet 模型的训练效果良好。
六、模型预测
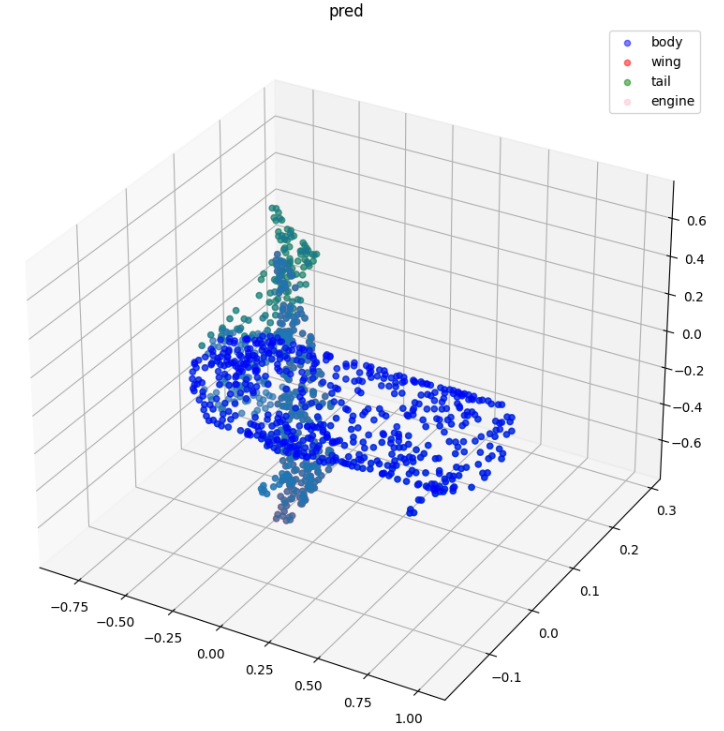
通过模型预测结果可知,飞机零件被不同颜色的点云进行良好分割,并且预测(pred)与标签(label)结果几乎一样,说明预测结果很好,模型的架构效果良好。
# 指定最佳模型参数的路径
ckpt_path = 'output/best_model.pdparams'
# 加载网络和参数
para_state_dict = paddle.load(ckpt_path)
model = PointNet()
model.set_state_dict(para_state_dict)
model.eval()
# 加载数据集中的点云数据
point_cloud = point_clouds[0]
show_point_cloud = point_cloud # 用于可视化的原始点云数据
point_cloud = paddle.to_tensor(np.reshape(point_cloud, (1, 1, 1024, 3)), dtype='float32') # 转换为Tensor并增加batch维度
label = point_clouds_labels[0]
# 前向推理获取预测结果
preds = model(point_cloud)
show_pred = paddle.argmax(preds, axis=-1).numpy() + 1 # 转换为numpy数组,并将预测结果从0开始编号调整为从1开始
# 可视化预测结果和真实标签
visualize_data(show_point_cloud, show_pred[0], 'pred')
visualize_data(show_point_cloud, label, 'label')

七、总结
本项目从点云数据的分析出发,利用 Paddle 框架,实现了数据集构建、模型组网、训练和预测的全流程开发。项目主要针对飞机零件的 3D 点云数据,进行精确的 part segmentation 任务。通过 PointNet 分类网络,模型能够有效地理解和处理点云数据中的空间信息,实现对飞机零件的细致分割。该项目不仅包括数据预处理和增强,还涉及模型优化和超参数调整,从而提升分割精度和效率,具有重要的工程应用价值和研究意义。
尽管如此,项目也存在一些不足:数据集规模和多样性有限,限制了模型的泛化能力。3D 点云数据处理和模型训练需要大量计算资源,对硬件配置要求较高。此外,PointNet 模型复杂性较高,导致其可解释性不足。点云数据易受噪声和缺失点影响,降低了模型处理低质量数据的能力,同时实时处理能力也有待提高。
未来可以通过扩大数据集规模和多样性、优化计算资源使用、提升模型可解释性、增强鲁棒性和抗噪性以及引入并行计算等技术,进一步提升模型的精度和效率。同时,将模型应用于汽车零件、建筑构件和医疗器械等其他需要精细分割的领域,扩展项目的应用范围和影响力。通过这些改进,项目将在点云数据处理领域贡献更多创新和实践经验。







![[leetcode]minimum-absolute-difference-in-bst 二叉搜索树的最小绝对差](https://img-blog.csdnimg.cn/direct/0df5dba0258a4927b8d0961be46a87f2.png)
![[吃瓜教程]南瓜书第4章决策树](https://img-blog.csdnimg.cn/direct/2d627345373f464490e8e676e718d806.png)