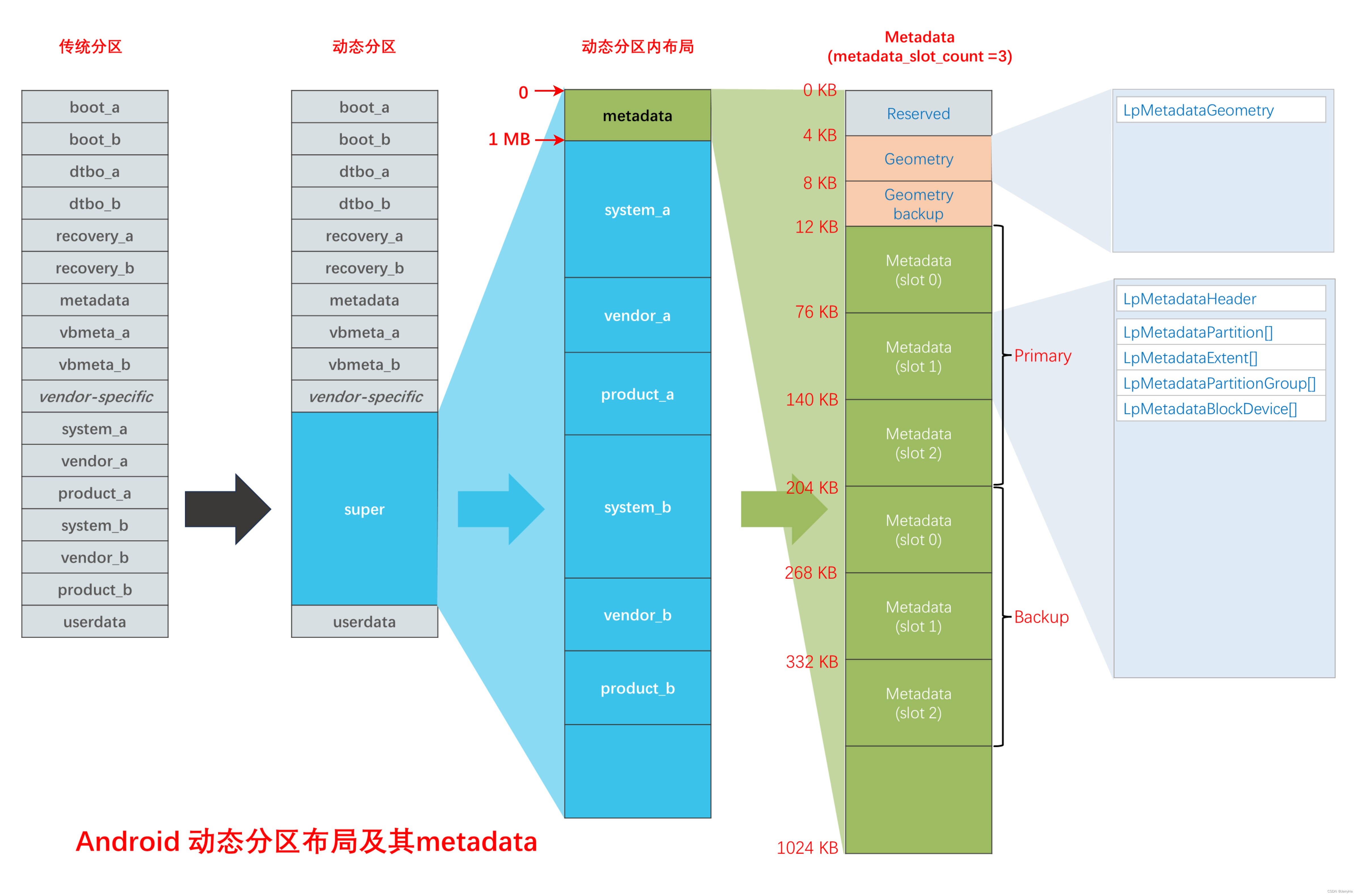
说明:
- 使用控件:DevExpress V24.1.3(链接:https://pan.baidu.com/s/1FosVrpyE7q_XvwhZK7ad3w?pwd=tw64提取码:tw64)
- 项目地址:https://github.com/VinciYan/Diagram_NET.git
- 可以帮助学习和理解数据结构图的最短路径算法等,适用于计算机专业大学生、大学教师和数据结构学习者等
- 不足之处,还望指出
简介
最短路径算法——Dijkstra算法
Dijkstra算法用于找到从单个源节点到图中所有其他节点的最短路径,适用于加权图(边有权重),但权重必须是非负的
步骤:
- 初始化起点到自身的距离为0,其他节点的距离为∞
- 将起点标记为已访问,所有其他节点为未访问
- 对于当前节点,检查所有相邻节点的未访问节点,计算其到起点的距离。如果这个距离小于当前记录的距离,就更新它
- 选择未访问节点中距离起点最近的节点作为下一个当前节点,重复步骤3
- 直到所有节点都被访问过
QuikGraph
QuikGraph是一个用于C#的强大且灵活的图数据结构和算法库。它提供了多种图表示形式和常见的图算法,可以轻松地在.NET应用程序中处理图形数据
主要特性
- 多种图类型:支持有向图、无向图、多重图等多种图类型
- 丰富的算法:包括遍历、最短路径、最大流、最小生成树等常见的图算法
- 灵活的接口:通过接口定义图的数据结构,使得用户可以自定义图的实现
- 良好的性能:经过优化,适用于处理大规模图数据
DevExpress的DiagramControl
DevExpress的DiagramControl是一个强大的控件,允许开发者在WinForms和WPF应用程序中创建、编辑和显示复杂的图表和流程图。它提供了多种工具和功能,帮助用户以交互和直观的方式构建和管理图形化数据表示
主要特性
- 支持多种图表类型:包括流程图、组织结构图、状态图等
- 丰富的图元库:提供预定义的形状、连接线和图元,用户也可以自定义图元
- 交互功能:支持拖放、缩放、旋转、对齐、分组等交互操作
- 数据绑定:可以绑定到数据源,动态生成图表
- 导入/导出:支持将图表导出为多种格式(如 PNG、JPEG、SVG、PDF 等),以及从多种格式导入
- 布局算法:内置多种自动布局算法,如树形布局、层次布局等
- 事件处理:丰富的事件模型,方便开发者处理用户交互和自定义行为
- 主题支持:与 DevExpress 其他控件一致,支持多种主题和样式
项目重点
需求
- 节点:能从元件工具栏拖拽节点元件到绘制区域完成绘制节点,在节点属性栏自定义节点编号
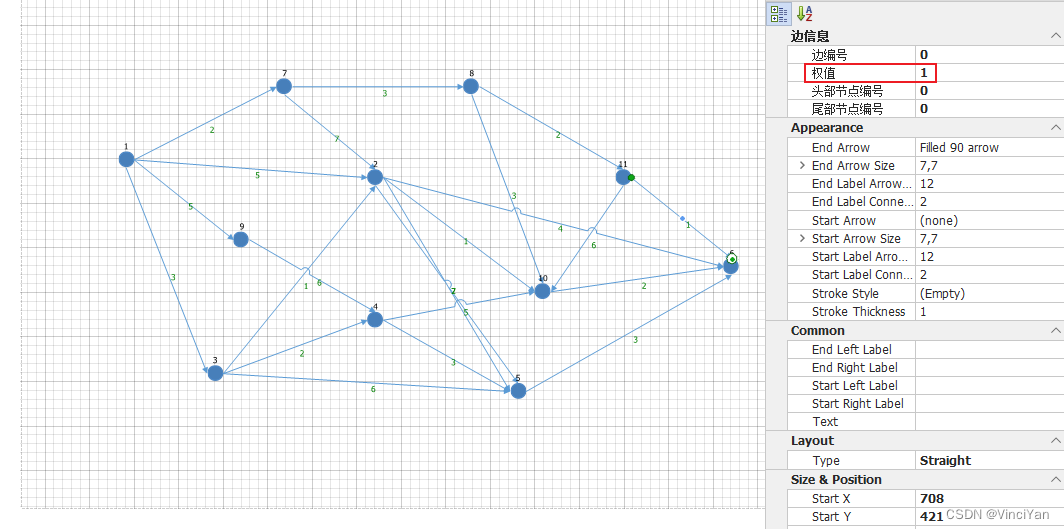
- 边:能够绘制有向边,在边属性栏自定义边的权值
- 最短路径可视化:完整显示最短路径
- 额外信息显示:显示节点编号和边的权值
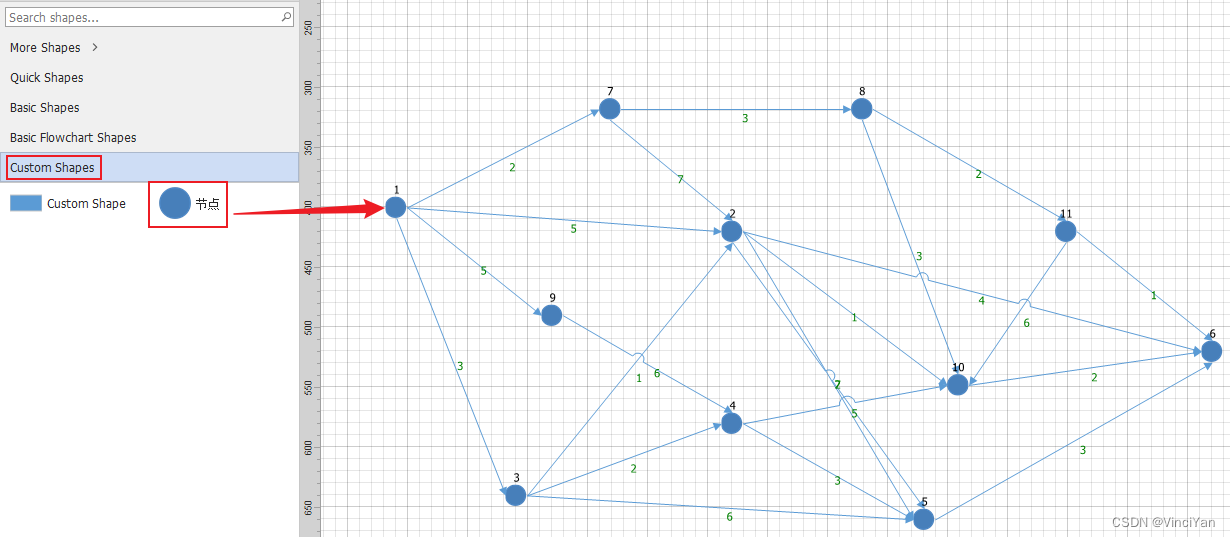
自定义元件工具栏
自定义元件工具栏,工具栏定义我们用于绘制图节点的元件,可以自定义元件的背景图片和显示文字等
然后就可以从工具栏拖拽该元件到右侧绘图区域完成图节点的绘制
var stencil = new DevExpress.Diagram.Core.DiagramStencil("CustomStencil", "Custom Shapes");
//注册DiagramShapeEx
var itemTool = new FactoryItemTool("CustomShape", () => "Custom Shape", diagram => { DiagramShapeEx customShape = new DiagramShapeEx() { Width = 100, Height = 50 }; return customShape; }, new System.Windows.Size(100, 50), false);
stencil.RegisterTool(itemTool);
// 注册ShapeImage
stencil.RegisterTool(new FactoryItemTool("节点", () => "节点", diagram =>
{
return new ShapeImage();
}, new System.Windows.Size(18, 18)));
DevExpress.Diagram.Core.DiagramToolboxRegistrator.RegisterStencil(stencil);
DiagramControl.ItemTypeRegistrator.Register(typeof(DiagramShapeEx), typeof(ShapeImage), typeof(CustomConnector));
自定义节点
可以继承DiagramImage,并自定义连接点,用于边的绘制边时作为边的起点或终点,并且在节点属性栏增加属性“Id”作为节点的唯一编号
public class ShapeImage : DiagramImage, IShape
{
public ShapeImage()
{
Image = Properties.Resource.node;
#region 设置连接点
List<PointFloat> points = new List<PointFloat>();
points.Add(new PointFloat(0f, 0.5f));
points.Add(new PointFloat(1f, 0.5f));
points.Add(new PointFloat(0.5f, 0f));
points.Add(new PointFloat(0.5f, 1f));
ConnectionPoints = new PointCollection(points);
#endregion
}
[XtraSerializableProperty, Category("自定义"), DisplayName("节点ID")]
public int Id { get; set; }
static ShapeImage()
{
DiagramControl.ItemTypeRegistrator.Register(typeof(ShapeImage));
}
}
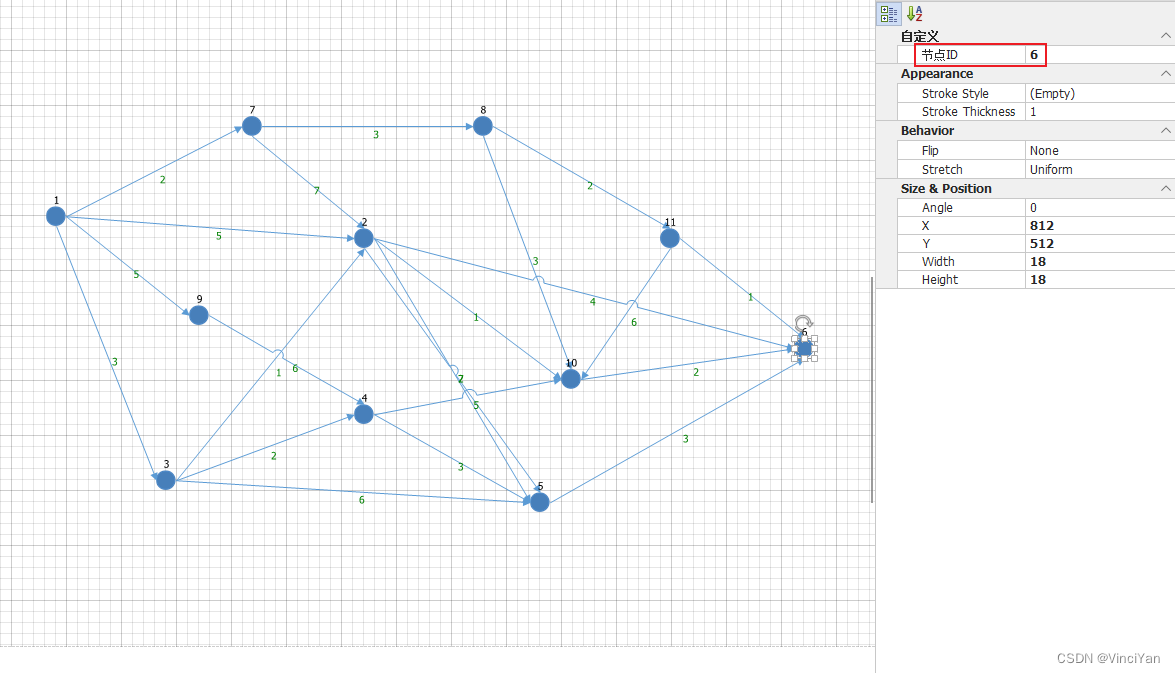
如图所示,节点6的属性新增了自定义属性“节点ID”
自定义边
继承DiagramConnector,自定义属性“权值”用于设置边的权值
public class CustomConnector : DiagramConnector, IShape
{
public CustomConnector()
{
}
[XtraSerializableProperty, Category("边信息"), DisplayName("边编号")]
public int Id { get; set; }
[XtraSerializableProperty, Category("边信息"), DisplayName("权值")]
public int WeightVal { get; set; }
[XtraSerializableProperty, Category("边信息"), DisplayName("头部节点编号")]
public int BeginNodeNo { get; set; }
[XtraSerializableProperty, Category("边信息"), DisplayName("尾部节点编号")]
public int EndNodeNo { get; set; }
static CustomConnector()
{
DiagramControl.ItemTypeRegistrator.Register(typeof(CustomConnector));
}
}
显示信息
默认绘制完成是不显示信息,可以新增显示功能,更方便设置和查看节点编号和边权值等
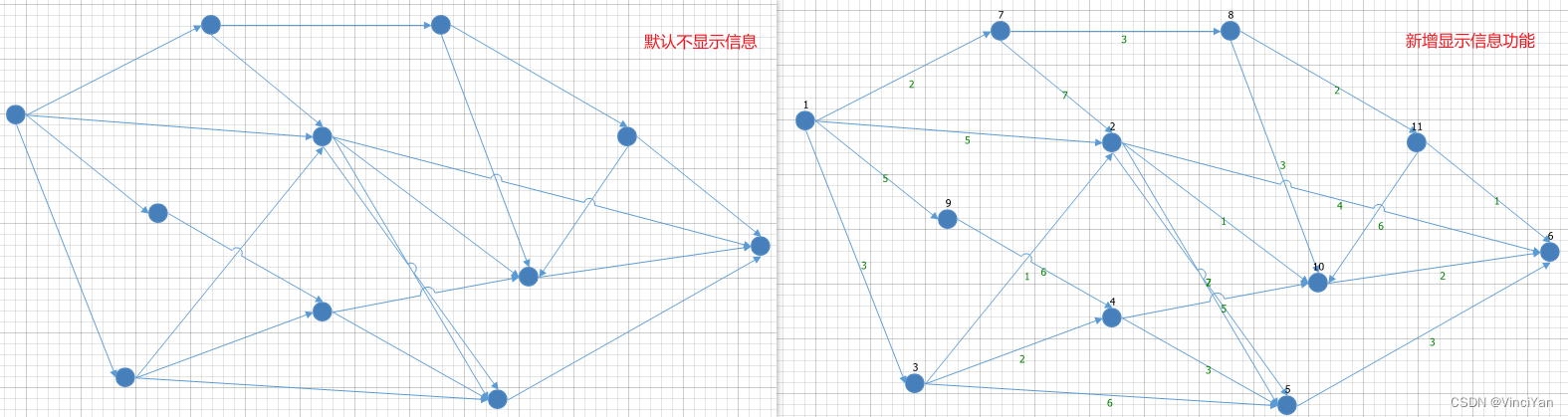
基本思路是绘制不可以被鼠标选择的DiagramShape用来显示编号和权值等信息
DiagramItemCollection diagramItemCollection = diagramControl1.Items;
foreach (var item in diagramItemCollection)
{
if (item is null) continue;
if (item is CustomConnector)
{
var con = (item) as CustomConnector;
var beginRec = con.ActualBeginPoint;
var endRec = con.ActualEndPoint;
var delX = endRec.X - beginRec.X;
var delY = endRec.Y - beginRec.Y;
nodeInfoShapes.Add(
new NodeInfoShape()
{
Content = con.WeightVal.ToString(),
FontColor = Color.Green,
Width = 15,
Height = 10,
CenterX = (float)(endRec.X),
CenterY = (float)(endRec.Y),
X = (float)((beginRec.X + endRec.X) * 0.5),
Y = (float)((beginRec.Y + endRec.Y) * 0.5),
}
);
continue;
}
var shape = (item) as IShape;
if (shape != null)
{
var rect = item.Bounds;
nodeInfoShapes.Add(
new NodeInfoShape()
{
Content = shape.Id.ToString(),
FontColor = Color.Black,
Width = 60,
Height = 20,
CenterX = (float)(rect.X + rect.Width * 0.5),
CenterY = (float)(rect.Y - NODE_NAME_Y_OFFSET),
X = (float)(rect.X + rect.Width * 0.5 - 60.0 * 0.5),
Y = (float)(rect.Y - NODE_NAME_Y_OFFSET - 20.0 * 0.5),
}
);
}
}
foreach (var item in nodeInfoShapes)
{
DiagramShape diagramShape = new DiagramShape()
{
Content = item.Content,
Width = item.Width,
Height = item.Height,
CanSelect = false,
CanEdit = false,
CanResize = false,
Position = new PointFloat(item.X, item.Y),
Appearance =
{
BackColor = Color.Transparent, FontSizeDelta = -1, ForeColor = item.FontColor,
BorderSize = 0
},
CanSnapToThisItem = false,
CanAttachConnectorBeginPoint = false,
CanAttachConnectorEndPoint = false,
CanCopy = false,
CanMove = false,
CanDelete = false,
CanRotate = false,
Tag = "info"
};
diagramControl1.Items.Add(diagramShape);
}
最短路径算法
这里使用QuikGraph类库来实现
public static List<PathDistanceRec> GetShortestPath(AdjacencyGraph<string, SEquatableTaggedEdge<string, double>> graph,
string start, string end)
{
List<PathDistanceRec> pathDistanceRecs = new List<PathDistanceRec>();
// 使用 Dijkstra 算法找到最短路径
var algorithm = new DijkstraShortestPathAlgorithm<string, SEquatableTaggedEdge<string, double>>(graph, edge => edge.Tag);
var predecessors = new VertexPredecessorRecorderObserver<string, SEquatableTaggedEdge<string, double>>();
// 指定起点
string source = start;
using (predecessors.Attach(algorithm))
{
algorithm.Compute(source);
foreach (var ver in graph.Vertices)
{
if (ver != source && ver == end && algorithm.TryGetDistance(ver, out double distance))
{
List<PathEdge> pathEdges = new List<PathEdge>();
List<string> pathList = new List<string>();
PathDistanceRec pathDistanceRec = new PathDistanceRec();
pathDistanceRec.StartEnd = source + "->" + end;
pathDistanceRec.Start = source;
pathDistanceRec.End = end;
pathDistanceRec.Dis = distance;
IEnumerable<SEquatableTaggedEdge<string, double>> path;
predecessors.TryGetPath(end, out path);
if (path == null) return null;
pathDistanceRec.Path = string.Join(",", path);
foreach (var step in path)
{
pathList.Add(step.Source);
pathEdges.Add(new PathEdge(step.Source, step.Target));
}
pathList.Add(end);
pathDistanceRecs.Add(pathDistanceRec);
pathDistanceRec.PathList = pathList;
pathDistanceRec.PathEdges = pathEdges;
}
}
}
return pathDistanceRecs;
}
效果
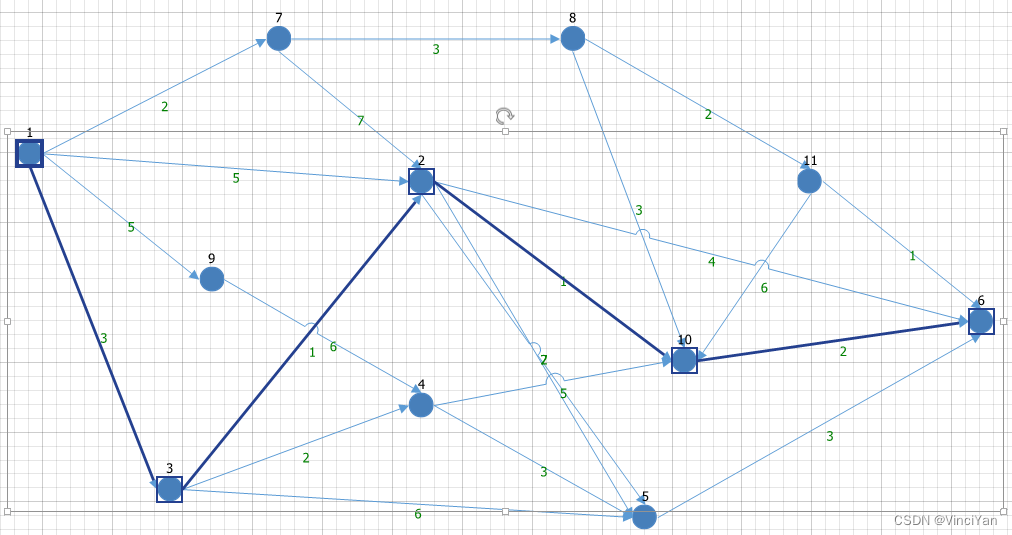
键盘同时按住Ctrl+Shift键,鼠标任意选择起点和终点,程序自动计算出最短路径并可视化最短路径
如下,起点为1,终点为6
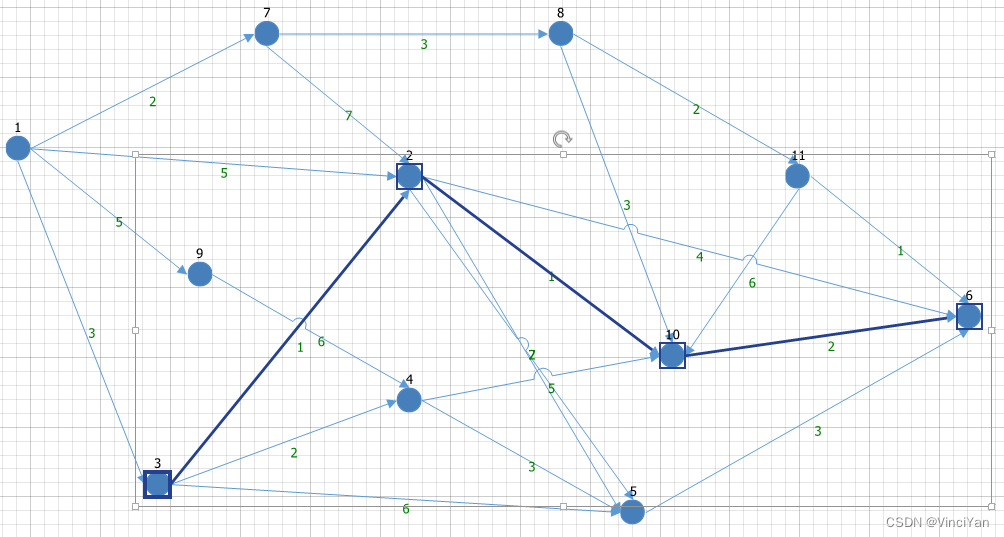
起点为3,终点为6

![[leetcode]minimum-absolute-difference-in-bst 二叉搜索树的最小绝对差](https://img-blog.csdnimg.cn/direct/0df5dba0258a4927b8d0961be46a87f2.png)
![[吃瓜教程]南瓜书第4章决策树](https://img-blog.csdnimg.cn/direct/2d627345373f464490e8e676e718d806.png)