[吃瓜教程]南瓜书第4章决策树

news2024/11/18 9:26:07

1.决策树的算法原理

  • 从逻辑角度，条件判断语句的组合；
  • 从几何角度，根据某种准则划分特征空间；
    是一种分治的思想，其最终目的是将样本约分约纯，而划分的核心是在条件的选择或者说是**特征空间的划分标准 **

2.信息熵

1）自信息：
I ( X ) = − l o g b p ( x ) I(X)=-log_bp(x) I(X)=−logb​p(x)
当b=2时单位为bit，当b=e时单位为nat
2）信息熵（自信息的期望）： 度量随机变量X的不确定性，信息熵越大越不确定
H ( X ) = E [ I ( X ) ] = − ∑ x p ( x ) l o g b p ( x ) H(X)=E[I(X)]=-\sum_xp(x)log_bp(x) H(X)=E[I(X)]=−x∑​p(x)logb​p(x)
信息熵计算时约定：若p(x)=0,则 p ( x ) l o g b p ( x ) = 0 p(x)log_bp(x)=0 p(x)logb​p(x)=0.当X的某个取值的概率为1时信息熵最小，值为0，当X的各个取值的概率均等时信息熵最大，最不缺定，其值为 l o g b ∣ X ∣ log_b|X| logb​∣X∣,其中 ∣ X ∣ |X| ∣X∣表示X可能的取值个数。这里可以想象一个例子，一个正常的筛子，它的信息熵最大，而特制的六面都是六的筛子，因为值确定了，所以信息熵最小。
这里的信息熵的最大值的简单的做个推导,在随机变量X的各个取值的概率均等的情况下：
− ∑ x p ( x ) l o g b p ( x ) − − − − − − − − − − − = − p ( x ) l o g b p ∣ X ∣ ( x ) − − − − − − − − − − − = − 1 ∣ X ∣ l o g b ∣ X ∣ − ∣ X ∣ − − − − − − − − − − − = l o g b ∣ X ∣ -\sum_xp(x)log_bp(x)\newline -----------\newline =-p(x)log_bp^{|X|}(x)\newline -----------\newline =-\frac{1}{|X|}log_b|X|^{-|X|}\newline -----------\newline =log_b|X| −x∑​p(x)logb​p(x)−−−−−−−−−−−=−p(x)logb​p∣X∣(x)−−−−−−−−−−−=−∣X∣1​logb​∣X∣−∣X∣−−−−−−−−−−−=logb​∣X∣

将样本类别标记y视作随机变量，各个类别在样本集合D中的占比 p k ( k = 1 , 2 , . . . , ∣ y ∣ ) p_k(k=1,2,...,|y|) pk​(k=1,2,...,∣y∣)视作各个类别取值的概率，则样本集合D（随机变量y）的信息熵（底数取为2）为
E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k l o g 2 p k Ent(D)=-\sum^{|y|}_{k=1}p_klog_2p_k Ent(D)=−k=1∑∣y∣​pk​log2​pk​
此时的信息熵所代表的不确定性可以转换理解为集合内样本的纯度。理解一下，我们希望我们划分出来的空间内的样本的y的概率越大越好，这样我们就把各个y的不同值划分的很好了，这就对应了信息熵中的期望信息熵最小的情况，因此可以用信息熵来表示集合内样本的纯度，信息熵越小样本的纯度越高。
3）条件熵：
Y的信息熵关于概率分布X的期望，在已知X后Y的不确定性
H ( Y ∣ X ) = ∑ x p ( x ) H ( Y ∣ X = x ) H(Y|X)=\sum_xp(x)H(Y|X=x) H(Y∣X)=x∑​p(x)H(Y∣X=x)
从单个属性（特征）a的角度来看，假设其可能取值为 a 1 , a 2 , . . . , a V {a^1,a^2,...,a^V} a1,a2,...,aV, D v D^v Dv表示属性a取值为 a v ∈ a 1 , a 2 , . . . , a V a^v\in{a^1,a^2,...,a^V} av∈a1,a2,...,aV的样本集合， ∣ D v ∣ ∣ D ∣ \frac{|D^v|}{|D|} ∣D∣∣Dv∣​表示占比，那么在已知属性a的取值后，样本集合D的条件熵为
∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) \sum^V_{v=1}\frac{|D^v|}{|D|}Ent(D^v) v=1∑V​∣D∣∣Dv∣​Ent(Dv)
这里上下两部分的关系，其实下面的部分再更加具体的解释上面的式子。这里第二部分假设X是只有一个维度，也就是特征a，而随机变量X的取值，这里就是a的具体的取值会影响到Y的信息熵，也就是说， D v D \frac{D^v}{D} DDv​就是 p ( x ) p(x) p(x)，而 H ( Y ∣ X = x ) H(Y|X=x) H(Y∣X=x)就是 E n t ( D v ) Ent(D^v) Ent(Dv)。这样可能好理解一点？
4）信息增益
在已知属性（特征）a的取值后y的不确定性减少的量，也即纯度的提升：
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 D ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain(D,a)=Ent(D)-\sum_{v=1}^D\frac{|D^v|}{|D|}Ent(D^v) Gain(D,a)=Ent(D)−v=1∑D​∣D∣∣Dv∣​Ent(Dv)

3.决策树

3.1ID3决策树

以信息增益为准则来选择划分属性的决策树
a ∗ = arg max ⁡ a ∈ A G a i n ( D , a ) a_*=\argmax_{a\in A} Gain(D,a) a∗​=a∈Aargmax​Gain(D,a)
ID3的问题：使用信息增益准则对可能取值数目较多的属性 有所偏好
代码：

# 导入必要的库
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
import matplotlib.pyplot as plt

# 加载西瓜数据集
data = {
    "编号": [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13],
    "色泽": ["青绿", "乌黑", "乌黑", "青绿", "浅白", "青绿", "乌黑", "浅白", "青绿", "浅白", "乌黑", "浅白", "青绿"],
    "根蒂": ["蜷缩", "蜷缩", "蜷缩", "蜷缩", "蜷缩", "稍蜷", "稍蜷", "稍蜷", "硬挺", "硬挺", "硬挺", "蜷缩", "蜷缩"],
    "敲声": ["浊响", "沉闷", "浊响", "沉闷", "浊响", "浊响", "浊响", "浊响", "清脆", "清脆", "清脆", "浊响", "浊响"],
    "纹理": ["清晰", "清晰", "清晰", "清晰", "清晰", "稍糊", "稍糊", "稍糊", "清晰", "清晰", "稍糊", "模糊", "稍糊"],
    "脐部": ["凹陷", "凹陷", "凹陷", "凹陷", "凹陷", "稍凹", "稍凹", "稍凹", "平坦", "平坦", "平坦", "稍凹", "稍凹"],
    "触感": ["硬滑", "硬滑", "硬滑", "硬滑", "硬滑", "软粘", "硬滑", "硬滑", "软粘", "硬滑", "硬滑", "硬滑", "硬滑"],
    "好瓜": ["是", "是", "是", "是", "否", "否", "否", "否", "否", "否", "否", "否", "否"]
}

# 转换为DataFrame
df = pd.DataFrame(data)

# 将'好瓜'列转换为二进制值
df['好瓜'] = df['好瓜'].map({'是': 1, '否': 0})

# 特征和目标变量
features = df.drop(['编号', '好瓜'], axis=1)
target = df['好瓜']

# 使用get_dummies进行one-hot编码
features_encoded = pd.get_dummies(features)

# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(features_encoded, target, test_size=0.3, random_state=42)

# 初始化决策树分类器（使用ID3算法）
clf = DecisionTreeClassifier(criterion='entropy', random_state=42)

# 训练模型
clf.fit(X_train, y_train)

# 预测测试集
y_pred = clf.predict(X_test)

# 计算准确率
accuracy = clf.score(X_test, y_test)
print(f'模型的准确率是: {accuracy*100:.2f}%')

# 可视化决策树
plt.figure(figsize=(20,10))
tree.plot_tree(clf, filled=True, feature_names=features_encoded.columns, class_names=['否', '是'])
plt.show()

# 存储决策树模型
import joblib
joblib.dump(clf, 'decision_tree_model.pkl')

# 加载模型并进行预测（示例）
loaded_model = joblib.load('decision_tree_model.pkl')
sample_data = X_test.iloc[0].values.reshape(1, -1)
prediction = loaded_model.predict(sample_data)
print(f'预测结果: {"是" if prediction[0] == 1 else "否"}')

可视化决策树：
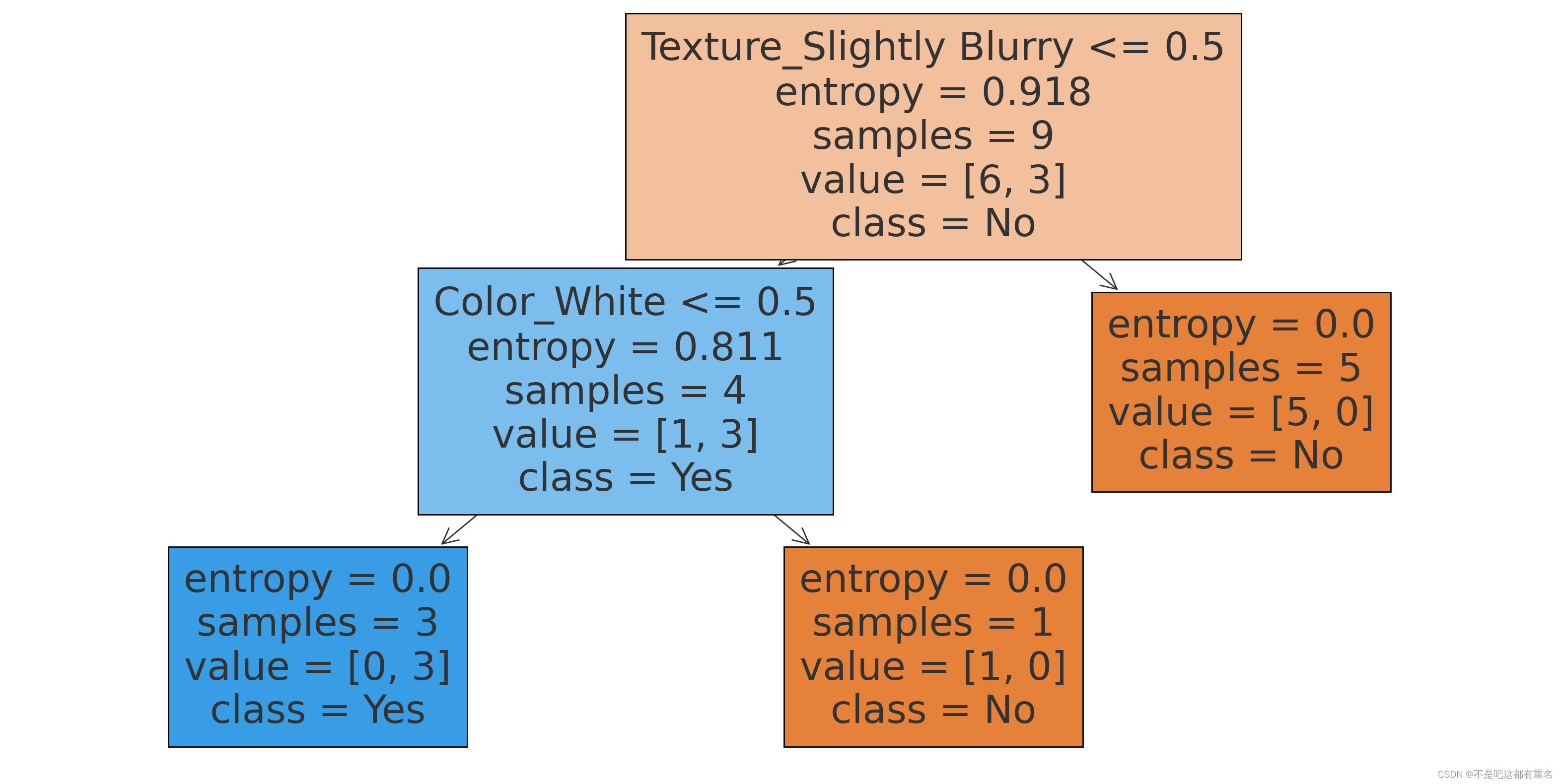
请添加图片描述

3.2 C4.5决策树

为了解决ID3的问题，C4.5使用增益率代替信息增益，增益率的定义如下：
G a i n r a t e ( D , a ) = G a i n ( D , a ) I V ( a ) Gain_rate(D,a)=\frac{Gain(D,a)}{IV(a)} Gainr​ate(D,a)=IV(a)Gain(D,a)​
其中，
I V ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ IV(a)=-\sum_{v=1}^V\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|} IV(a)=−v=1∑V​∣D∣∣Dv∣​log2​∣D∣∣Dv∣​
称为属性a的固有值，a的可能取值个数V越大，通常其固有值也越大。

C4.5的问题： 增益率对可能取值数目较少的属性有所偏好
因此，C4.5采用启发式方法：先选出信息增益高于平均水平的属性，然后再从中选择增益率最高的。
代码：

# 导入必要的库
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
import matplotlib.pyplot as plt

# 创建西瓜数据集
data = {
    "Number": [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13],
    "Color": ["Green", "Black", "Black", "Green", "White", "Green", "Black", "White", "Green", "White", "Black", "White", "Green"],
    "Root": ["Curled", "Curled", "Curled", "Curled", "Curled", "Slightly Curled", "Slightly Curled", "Slightly Curled", "Stiff", "Stiff", "Stiff", "Curled", "Curled"],
    "Knock": ["Dull", "Dull", "Dull", "Dull", "Dull", "Dull", "Dull", "Dull", "Clear", "Clear", "Clear", "Dull", "Dull"],
    "Texture": ["Clear", "Clear", "Clear", "Clear", "Clear", "Slightly Blurry", "Slightly Blurry", "Slightly Blurry", "Clear", "Clear", "Slightly Blurry", "Blurry", "Slightly Blurry"],
    "Navel": ["Indented", "Indented", "Indented", "Indented", "Indented", "Slightly Indented", "Slightly Indented", "Slightly Indented", "Flat", "Flat", "Flat", "Slightly Indented", "Slightly Indented"],
    "Touch": ["Hard and Smooth", "Hard and Smooth", "Hard and Smooth", "Hard and Smooth", "Hard and Smooth", "Soft and Sticky", "Hard and Smooth", "Hard and Smooth", "Soft and Sticky", "Hard and Smooth", "Hard and Smooth", "Hard and Smooth", "Hard and Smooth"],
    "Good": ["Yes", "Yes", "Yes", "Yes", "No", "No", "No", "No", "No", "No", "No", "No", "No"]
}

# 转换为DataFrame
df = pd.DataFrame(data)

# 将'Good'列转换为二进制值
df['Good'] = df['Good'].map({'Yes': 1, 'No': 0})

# 特征和目标变量
features = df.drop(['Number', 'Good'], axis=1)
target = df['Good']

# 使用get_dummies进行one-hot编码
features_encoded = pd.get_dummies(features)

# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(features_encoded, target, test_size=0.3, random_state=42)

# 初始化决策树分类器（使用C4.5算法，即使用信息增益比）
clf = DecisionTreeClassifier(criterion='entropy', random_state=42, splitter='best')

# 训练模型
clf.fit(X_train, y_train)

# 可视化决策树
plt.figure(figsize=(20,10))
tree_plot = tree.plot_tree(clf, filled=True, feature_names=features_encoded.columns, class_names=['No', 'Yes'])
plt.show()

可视化决策树：
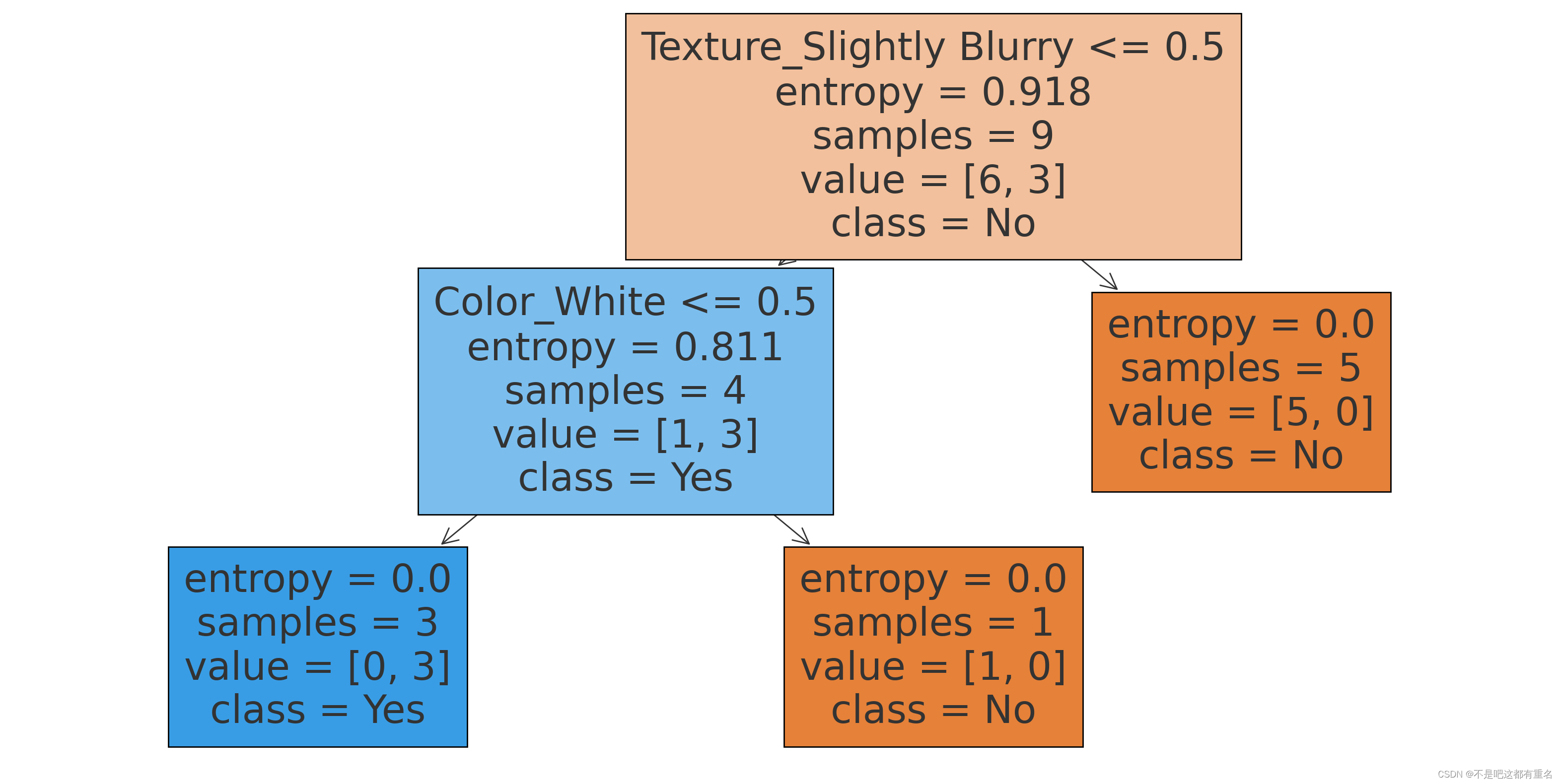
请添加图片描述

3.3CART决策树

基尼值： 从样本集合D中随机抽取两个样本，其类别标记不一致的概率。因此，基尼值越小，碰到异类的概率就越小，纯度自然越高。（对应信息熵）
G i n i ( D ) = ∑ k = 1 ∣ y ∣ ∑ k ′ ≠ k p k p k ′ = ∑ k = 1 ∣ y ∣ p k ( 1 − p k ) = 1 − ∑ k = 1 ∣ y ∣ p k 2 Gini(D)=\sum_{k=1}^{|y|}\sum_{k'\neq k}p_kp_{k'}=\sum_{k=1}^{|y|}p_k(1-p_k)=1-\sum^{|y|}_{k=1}p_k^2 Gini(D)=k=1∑∣y∣​k′=k∑​pk​pk′​=k=1∑∣y∣​pk​(1−pk​)=1−k=1∑∣y∣​pk2​
基尼指数： 属性a的基尼指数(对应条件熵)：
G i n i i n d e x ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ G i n i ( D v ) Gini_index(D,a)=\sum_{v=1}^V\frac{|D^v|}{|D|}Gini(D^v) Ginii​ndex(D,a)=v=1∑V​∣D∣∣Dv∣​Gini(Dv)

CART决策树： 选择基尼指数最小的属性作为最优划分属性，最后构造了一个二叉树。
a ∗ = arg max ⁡ a ∈ A G i n i _ i n d e x ( D , a ) a_*=\argmax_{a\in A} Gini\_index(D,a) a∗​=a∈Aargmax​Gini_index(D,a)
CART决策树的实际构造算法如下：

  • 对每个属性a的每个可能取值v，将数据集D分为a=v和a≠v两部分计算基尼指数，即
    G i n i i n d e x ( D , a ) = ∣ D a = v ∣ ∣ D ∣ G i n i ( D a = v ) + ∣ D a ≠ v ∣ ∣ D ∣ G i n i ( D a ≠ v ) Gini_index(D,a)=\frac{|D^{a=v}|}{|D|}Gini(D^{a=v})+\frac{|D^{a\neq v}|}{|D|}Gini(D^{a\neq v}) Ginii​ndex(D,a)=∣D∣∣Da=v∣​Gini(Da=v)+∣D∣∣Da=v∣​Gini(Da=v)
  • 选择基尼指数最小的属性及其对应取值作为最优划分属性和最优划分点；
  • 重复上述步骤，直至满足停止条件

代码：

# 导入必要的库
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
import matplotlib.pyplot as plt

# 创建西瓜数据集
data = {
    "Number": [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13],
    "Color": ["Green", "Black", "Black", "Green", "White", "Green", "Black", "White", "Green", "White", "Black", "White", "Green"],
    "Root": ["Curled", "Curled", "Curled", "Curled", "Curled", "Slightly Curled", "Slightly Curled", "Slightly Curled", "Stiff", "Stiff", "Stiff", "Curled", "Curled"],
    "Knock": ["Dull", "Dull", "Dull", "Dull", "Dull", "Dull", "Dull", "Dull", "Clear", "Clear", "Clear", "Dull", "Dull"],
    "Texture": ["Clear", "Clear", "Clear", "Clear", "Clear", "Slightly Blurry", "Slightly Blurry", "Slightly Blurry", "Clear", "Clear", "Slightly Blurry", "Blurry", "Slightly Blurry"],
    "Navel": ["Indented", "Indented", "Indented", "Indented", "Indented", "Slightly Indented", "Slightly Indented", "Slightly Indented", "Flat", "Flat", "Flat", "Slightly Indented", "Slightly Indented"],
    "Touch": ["Hard and Smooth", "Hard and Smooth", "Hard and Smooth", "Hard and Smooth", "Hard and Smooth", "Soft and Sticky", "Hard and Smooth", "Hard and Smooth", "Soft and Sticky", "Hard and Smooth", "Hard and Smooth", "Hard and Smooth", "Hard and Smooth"],
    "Good": ["Yes", "Yes", "Yes", "Yes", "No", "No", "No", "No", "No", "No", "No", "No", "No"]
}

# 转换为DataFrame
df = pd.DataFrame(data)

# 将'Good'列转换为二进制值
df['Good'] = df['Good'].map({'Yes': 1, 'No': 0})

# 特征和目标变量
features = df.drop(['Number', 'Good'], axis=1)
target = df['Good']

# 使用get_dummies进行one-hot编码
features_encoded = pd.get_dummies(features)

# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(features_encoded, target, test_size=0.3, random_state=42)

# 初始化决策树分类器（使用CART算法，即使用Gini系数）
clf_cart = DecisionTreeClassifier(criterion='gini', random_state=42)

# 训练模型
clf_cart.fit(X_train, y_train)

# 预测测试集
y_pred_cart = clf_cart.predict(X_test)

# 计算准确率
accuracy_cart = clf_cart.score(X_test, y_test)
print(f'模型的准确率是: {accuracy_cart*100:.2f}%')

# 可视化决策树
plt.figure(figsize=(20,10))
tree_plot_cart = tree.plot_tree(clf_cart, filled=True, feature_names=features_encoded.columns, class_names=['No', 'Yes'])
plt.show()

可视化决策树：
请添加图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1884198.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Fooocus模型配置中文教程

Fooocus模型配置中文教程

很多同学这里不知道该怎么选择。不知道每个模型效果，针对这个整理了一个表格。参考表格就可生成预期效果图。 下载地址： https://download.csdn.net/download/yuanshiren133/89503764
阅读更多...
【详解】RV1106移植opencv-mobile库

【详解】RV1106移植opencv-mobile库

文章目录 前言一、烧入镜像二、编译项目1.创建项目文件 三、移植四、运行文件五、总结 前言 硬件：瑞芯微Rv1106【Luckfox Pro\Max Pico、网线一根、USB线、串口助手、摄像头 软件：ubuntu 20.4 编译器：arm-rockchip830-linux-uclibcgnueabihf…
阅读更多...
Cesium大屏-vue3注册全局组件

Cesium大屏-vue3注册全局组件

1.需求 说明：产品经理要求开发人员在地图大屏上面随意放置组件，并且需要通过数据库更改其组件大小，位置等；适用于大屏组件中场站视角、任意位置标题等。 2.实现 2.1GlobalComponents.vue 说明：containerList可以通…
阅读更多...
阿里云物联网应用层开发：第三部分，微信小程序和web客户端实现

阿里云物联网应用层开发：第三部分，微信小程序和web客户端实现

文章目录 哔哩哔哩视频教程1、阿里云物联网平台对接微信小程序2、阿里云物联网平台对接web客户端2-1MQTT服务器编写2-2 web端Servlet部分编写 哔哩哔哩视频教程 【阿里云物联网综合开发，STM32ESP8266微信小程序web客户端一篇教程详细讲解】 https://www.bilibili.c…
阅读更多...
袋鼠快跳 - 常用网址快捷访问

袋鼠快跳 - 常用网址快捷访问

袋鼠快跳 开源地址：https://github.com/chenbimo/kangaroo-jump 袋鼠快跳，是一个以 简单快捷 为目标的网站快导航 油猴脚本。 本工具的理念就是，用最快的速度访问我们最常用的50个网站。 功能特点 完全免费，以 MIT协议 开源。…
阅读更多...
文生图功能介绍

文生图功能介绍

Stable Diffusion WebUI（SD WebUI）及文生图功能介绍 一、引言 随着人工智能技术的飞速发展，AI绘画作为一种新兴的艺术形式，逐渐走入人们的视野。Stable Diffusion WebUI（简称SD WebUI）作为AI绘画领域的重…
阅读更多...
如何现代的编译和安装内核

如何现代的编译和安装内核

前言：本文是在阅读书目时找到了一篇非常高质量的文章。的原文是英文，现在我自己手头翻译了一下，发布到这里。 原文连接：How to compile a Linux kernel in the 21st century | Opensource.com 目录 更新内核的现代方法 安装内…
阅读更多...
在线如何快速把图片变小？图片轻松修改大小的3个在线工具

在线如何快速把图片变小？图片轻松修改大小的3个在线工具

随着现在图片在工作和生活中的广泛使用，在使用图片的时候经常会因为图片太大的问题受到影响，比较简单的一种处理方法可以通过压缩图片的方式来缩小图片大小，那么图片压缩具体该怎么来操作呢？下面就给大家分享几款图片在线压缩工具…
阅读更多...
npm安装包报错解决

npm安装包报错解决

目录 一：问题回顾 二:问题分析 三：npm降级或者升级 四：npm和node js 关系 一：问题回顾 今天在本地部署一个vue开发的项目，需要在本地看下运行情况，按照常规的操作就是在网站根目录运行npm install 安装…
阅读更多...
Android super.img结构及解包和重新组包

Android super.img结构及解包和重新组包

Android super.img结构及解包和重新组包 从Android10版本开始，Android系统使用动态分区，system、vendor、 odm等都包含在super.img里面，编译后的最终镜像不再有这些单独的 image，取而代之的是一个总的 super.img. 1. 基础知识 …
阅读更多...
LVS-负载均衡

LVS-负载均衡

目录 一、概念 二、LVS工作原理 1. ipvs/ipvsadm 2.名词： 三、常用命令 四、工作模式 1.NAT地址转换模式 （1）工作流程 （2）特点 （3）实验过程 a.环境准备： b.修改测试机的…
阅读更多...
第二周：计算机网络概述（下）

第二周：计算机网络概述（下）

一、计算机网络性能指标（速率、带宽、延迟） 1、速率 2、带宽 3、延迟/时延 前面讲分组交换的时候介绍了，有一种延迟叫“传输延迟”，即发送一个报文，从第一个分组的发送，到最后一个分组的发送完成的这段时…
阅读更多...
vue3.2及以上 父调子的方法defineExpose定义供父调用的方法及属性

vue3.2及以上 父调子的方法defineExpose定义供父调用的方法及属性

1、定义子类LoginForm&#xff1a; function handleLogin(account, token) {console.log(account,token)}defineExpose({handleLogin,}); 2、父类调用子类组件 const loginFormRef ref(); <LoginForm ref"loginFormRef" />loginFormRef.value.handleLogin(…
阅读更多...
仓库管理系统23--用户管理

仓库管理系统23--用户管理

原创不易&#xff0c;打字不易&#xff0c;截图不易&#xff0c;多多点赞&#xff0c;送人玫瑰&#xff0c;留有余香&#xff0c;财务自由明日实现 1、创建用户管理的用户控件 <UserControl x:Class"West.StoreMgr.View.UserInfoView"xmlns"http://schemas.…
阅读更多...
SSE代替轮询？

SSE代替轮询？

什么是 SSE SSE&#xff08;Server-Sent Events&#xff0c;服务器发送事件&#xff09;&#xff0c;为特定目的而扩展的 HTTP 协议&#xff0c;用于实现服务器向客户端推送实时数据的单向通信。如果连接断开&#xff0c;浏览器会自动重连&#xff0c;传输的数据基于文本格式。…
阅读更多...
C语言入门-指针和数组5

C语言入门-指针和数组5

指针和地址 地址 地址是内存中一个特定位置的标识符。每个内存位置都有一个唯一的地址&#xff0c;用于存储数据。这些地址通常表示为十六进制数。 物理地址&#xff1a;硬件层次上的实际内存地址。逻辑地址&#xff1a;程序运行时使用的地址&#xff0c;由操作系统管理。 …
阅读更多...
Edge浏览器添加新标签页网址为 百度 搜索

Edge浏览器添加新标签页网址为 百度 搜索

默认不能直接设置&#xff0c;需要安装New Tab Change插件 安装拓展插件 url 这里点击获取即可&#xff08;我已经安装过了&#xff09; 某些扩展会更改浏览器设置&#xff0c;例如默认搜索引擎、新选项卡页和其他类型的网站数据。 为了防止扩展更改在安装时设置的首选项Micr…
阅读更多...
MQ:RabbitMQ

MQ:RabbitMQ

同步和异步通讯 同步通讯: 需要实时响应,时效性强 耦合度高 每次增加功能都要修改两边的代码 性能下降 需要等待服务提供者的响应,如果调用链过长则每次响应时间需要等待所有调用完成 资源浪费 调用链中的每个服务在等待响应过程中,不能释放请求占用的资源,高并发场景下…
阅读更多...
来聊聊Redis定期删除策略的设计与实现

来聊聊Redis定期删除策略的设计与实现

写在文章开头 我们都知道redis通过主线程完成内存数据库的指令操作&#xff0c;由于只有一个线程负责核心业务流程&#xff0c;所以对于每一个操作都要求尽可能达到尽可能的高效迅速&#xff0c;而本文就基于源码来聊聊redis的定期删除策略的设计与实现。 Hi&#xff0c;我是 …
阅读更多...
上传头像到Domino中

上传头像到Domino中

大家好&#xff0c;才是真的好。 首先&#xff0c;说一个消息&#xff0c;2024年6月25号HCL发布了一则公告&#xff0c;就是从2024年12月10号开始结束Notes/Domino 11.0.x版本的市场订单申请&#xff0c;从从2025年6月26号开始停止对Notes/Domino 11.0.x版本的产品技术支持&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023