由初中的几何知识我们可以知道，确定一个三角形至少需要三个不共线的点，因此确定一个三角形的外接圆至少可用三个点。我们不妨假设三个点坐标为P1(x1,y1,z1),P2(x2,y2,z2),P3(x3,y3,z3)。
圆方程的标准形式为：
(xi-x)2+(yi-y)2=R2 （1）
在三维空间坐标系中球的方程为：
(xi-x)2+(yi-y)2+(zi-z)2=R2 （2）
一个空间圆的产生可以看作过该圆心的一个球体，被一个经过该点的平面所截而得到。因此在求取空间圆的时候还应添加平面约束方程，以上述P1、P2、P3三个不共线的点可以确定一个平面，平面方程为：
AX+BY+CZ+D=0 (3)
求解方程(3)时注意技巧，常用两种方式，向量法或者待定系数法。若使用待定系数法则需平面方程的另一种形式,点法式为：
A(x-x0)+B(y-y0)+C(z-z0)=0 (4)
但是笔者建议使用向量的方式，更为简单方便，三点在同一个平面上，以P1为基点，寻找两条向量P12、P13；该平面方程的法向量为n=P12×P13（注:向量的叉乘）。在得到平面的法向量之后，带入其中一个点到方程(4)中即可得到平面约束方程。我们不妨将该约束方程系数设为A1、B1、C1、D1。
在得到约束平面方程之后还须求解空间中圆的方程，在求解圆的方程时也有诸多方式，一种方式为将已知点带入到方程(2)中，利用待定系数法求解,我们仍参以P1为方程的基点，分别将P2,P3带入可以得到如下方程：
(x1-x)2+(y1-y)2+(z1-z)2=R2
(x2-x)2+(y2-y)2+(z2-z)2=R2
(x3-x)2+(y3-y)2+(z3-z)2=R2
整理后可以得到
A2=2(x2-x1) ,B2=2(y2-y1) ,C2=2(z2-z1),D2=-(x12+y12+z12-x22-y22-z22) (5)
A3=2(x3-x1) ,B3=2(y3-y1) ,C3=2(z3-z1),D3=-(x12+y12+z12-x32-y32-z32) (6)
建立系数矩阵:

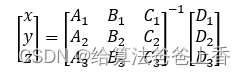
求解上述方程即可得到空间圆心坐标(x,y,z)。

RANSAC空间圆拟合的代码实现如下：

#include <iostream>
#include <pcl/io/pcd_io.h>
#include <pcl/point_types.h>
#include <pcl/common/distances.h>


int main()
{
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::io::loadPCDFile("circle_3D.pcd", *cloud);

	int iters = 100;					//迭代次数
	float F_thre = 0.1, D_thre = 0.1;	//点到空间圆所在平面的距离阈值，半径误差阈值
	int max_inner_count = 0;			//最大内点个数
	pcl::PointXYZ O;					//圆心
	float R;							//半径
	srand(time(0));						//随机数种子

	for (size_t i = 0; i < iters; i++)	//循环迭代
	{
		int n1 = rand() % cloud->size(), n2 = rand() % cloud->size(), n3 = rand() % cloud->size();
		pcl::PointXYZ p1 = cloud->points[n1], p2 = cloud->points[n2], p3 = cloud->points[n3];	//从点云随机取三个点

		float A1 = (p2.y - p1.y) * (p3.z - p1.z) - (p2.z - p1.z) * (p3.y - p1.y);	//计算空间圆所在平面方程
		float B1 = (p2.z - p1.z) * (p3.x - p1.x) - (p2.x - p1.x) * (p3.z - p1.z);
		float C1 = (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x);
		float D1 = -(A1 * p1.x + B1 * p1.y + C1 * p1.z);

		float A2 = 2 * (p2.x - p1.x);
		float B2 = 2 * (p2.y - p1.y);
		float C2 = 2 * (p2.z - p1.z);
		float D2 = p1.x * p1.x + p1.y * p1.y + p1.z * p1.z - p2.x * p2.x - p2.y * p2.y - p2.z * p2.z;

		float A3 = 2 * (p3.x - p1.x);
		float B3 = 2 * (p3.y - p1.y);
		float C3 = 2 * (p3.z - p1.z);
		float D3 = p1.x * p1.x + p1.y * p1.y + p1.z * p1.z - p3.x * p3.x - p3.y * p3.y - p3.z * p3.z;

		Eigen::Matrix3f A;
		A << A1, B1, C1, A2, B2, C2, A3, B3, C3;

		Eigen::Vector3f D;
		D << -D1, -D2, -D3;

		auto X = A.inverse() * D;

		pcl::PointXYZ p(X[0], X[1], X[2]);
		float r = (pcl::euclideanDistance(p, p1) + pcl::euclideanDistance(p, p2) + pcl::euclideanDistance(p, p3)) / 3;
		//std::cout << r << std::endl;
		int inner_count = 0;
		for (size_t i = 0; i < cloud->size(); i++)
		{
			float Fi = abs(A1 * cloud->points[i].x + B1 * cloud->points[i].y + C1 * cloud->points[i].z + D1) / sqrt(A1 * A1 + B1 * B1 + C1 * C1);	//点到平面距离
			float Di = abs(pcl::euclideanDistance(p, cloud->points[i]) - r);																		//点到圆心距离于半径差值
			if (Fi < F_thre && Di < D_thre)
				inner_count++;
		}
		if (inner_count > max_inner_count)	//如果本轮迭代内点个数更多，则更新圆心和半径
		{
			max_inner_count = inner_count;
			O = p;
			R = r;
		}
	}
	
	std::cout << O << " " << R << std::endl;

	return 0;
}

参考：在空间三维坐标系下的圆、直线和平面拟合