分组交叉验证是非常常见的一种交叉验证策略，它适用于数据中的分组高度相关时。比如我们想构建一个从人脸图片中识别情感的系统，并且收集了100个人的照片的数据集，其中每个人都进行了多次拍摄，分别展示了不同的情感。我们的目标是构架一个分类器，能够正确识别未包含在数据集中的人的情感。

我们可以使用默认的分层交叉验证来度量分类器的性能。但是这样的话，同一个人的照片可能同时出现在训练集和测试集中。对于分类器而言，检测训练集中出现过的人脸情感比全新的人脸要容易得多。因此，为了准确评估模型对新的人脸的泛化能力，我们必须确保训练集和测试集中包含不同人的图像。

为了实现这一点，我们可以使用GroupKFold，它以groups数组作为参数，可以用来说明照片中对应的是哪个人。这里的groups数组表示数据中的分组，在创建训练集和测试集的时候不应该将其分开，也不应该与类别标签弄混。

数据分组的这种例子常见于医疗应用，你可能拥有来自同一名病人的多个样本，但想要将其泛化到新的病人。同样的，在语音识别领域，你的数据集中可能包含同一名发言人的多条记录，但你希望能够识别到新的发言人的讲话。

下面的例子，用到了一个由groups数组制定分组的模拟数据集。这个数据集包含12个数据点，且对于每个数据点，groups指定了该点所属的分组。一共分成了4个组，前3个样本属于第一组，接下来的4个样本属于第二组，以此类推：

from sklearn.datasets import make_blobs
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GroupKFold

X,y=make_blobs(n_samples=12,random_state=0)
logreg=LogisticRegression()
groups=[0,0,0,1,1,1,1,2,2,3,3,3]

scores=cross_val_score(logreg,X,y=y,groups=groups,cv=GroupKFold(n_splits=3))
print('Cross-validation scores:\n{}'.format(scores))

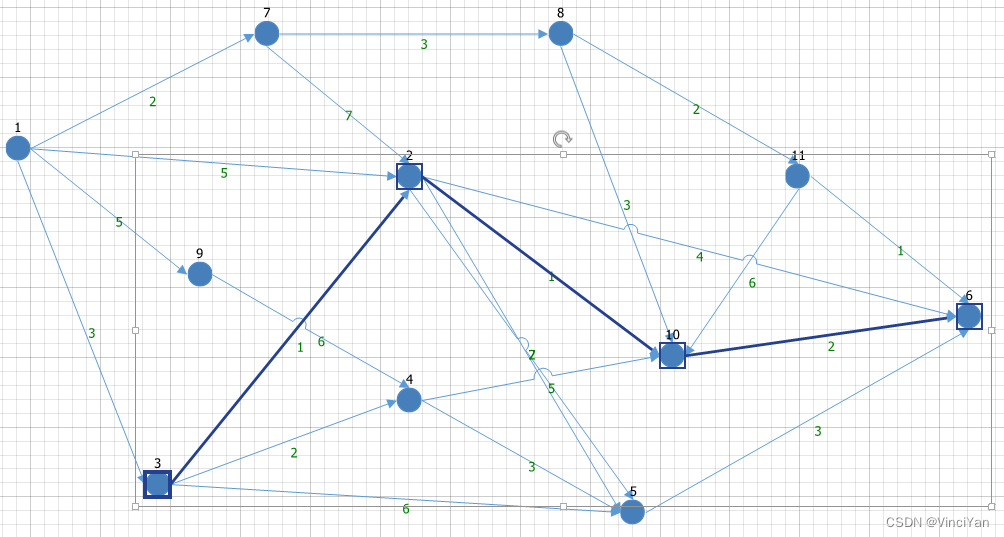
样本不需要按分组进行排序，我们这么做只是为了便于说明。基于这些标签计算得到的划分如下图：

mglearn.plots.plot_group_kfold()