matlab仿真通信信号和系统分析（上）

news2024/11/23 7:11:53

（内容源自详解MATLAB／SIMULINK 通信系统建模与仿真刘学勇编著第三章内容，有兴趣的读者请阅读原书）

一、求离散信号卷积和

主要还是使用卷积函数conv，值得注意的是，得到的卷积和长度结果为81，是两个原始序列长度相加-1（41+41-1）；

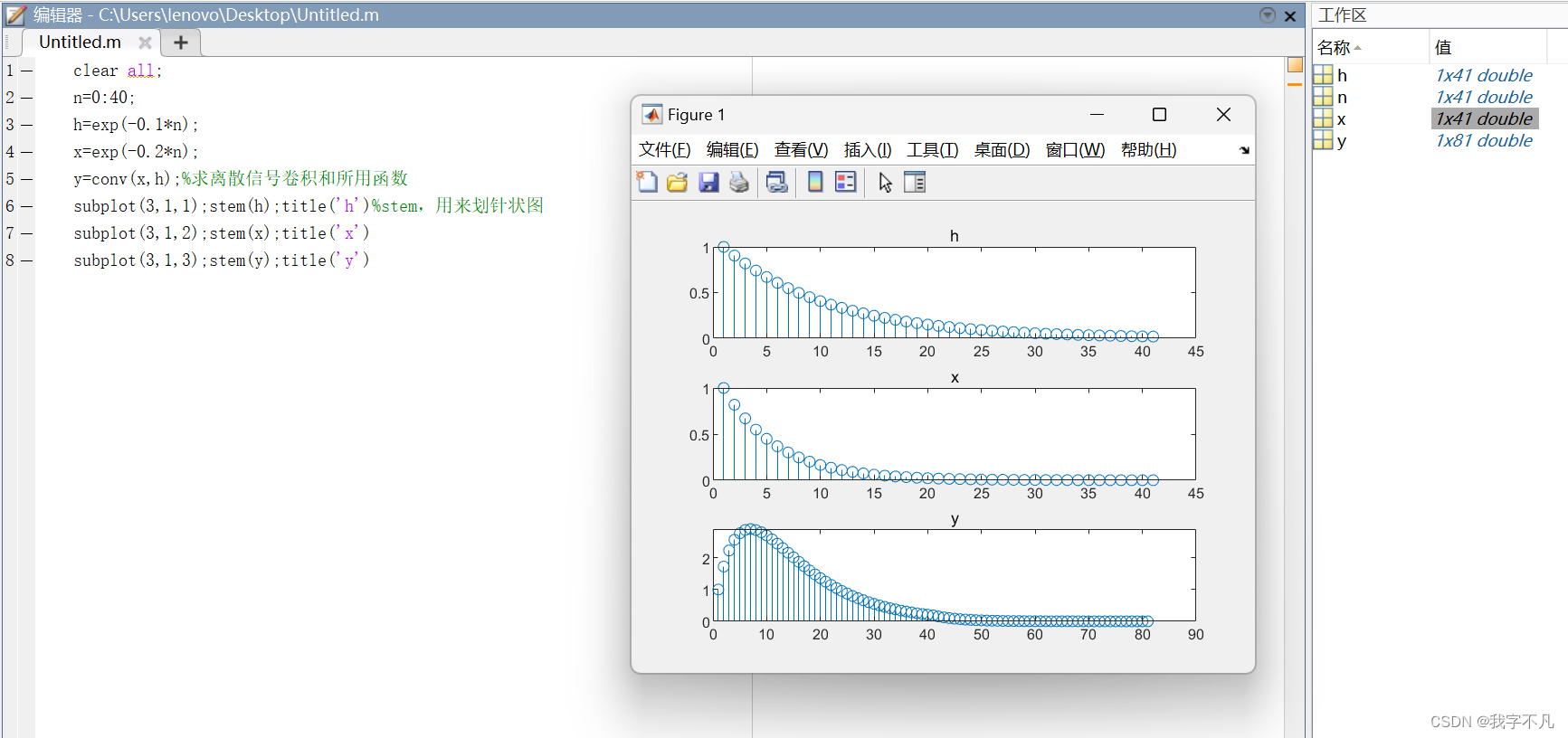
二、连续时间信号的傅里叶变换

使用函数fourier和函数ifourier进行傅里叶变换和傅里叶变换，可以注意到，将变量符号化后可以直接得到傅里叶变换后的数学表达式。

clear all;
syms t;%调用函数fourier和ifourier需要使用syms命令对涉及到的变量进行说明，将其说明为符号变量
f=t*exp(-abs(t));
subplot(1,2,1);ezplot(f);%函数fourier和ifourier得到的返回函数仍然是符号表达式，作图应使用ezplot函数（有冲激函数ezplot无法使用）
F=fourier(f)
subplot(1,2,2);ezplot(abs(F));%abs（F）用来做幅频特性的图像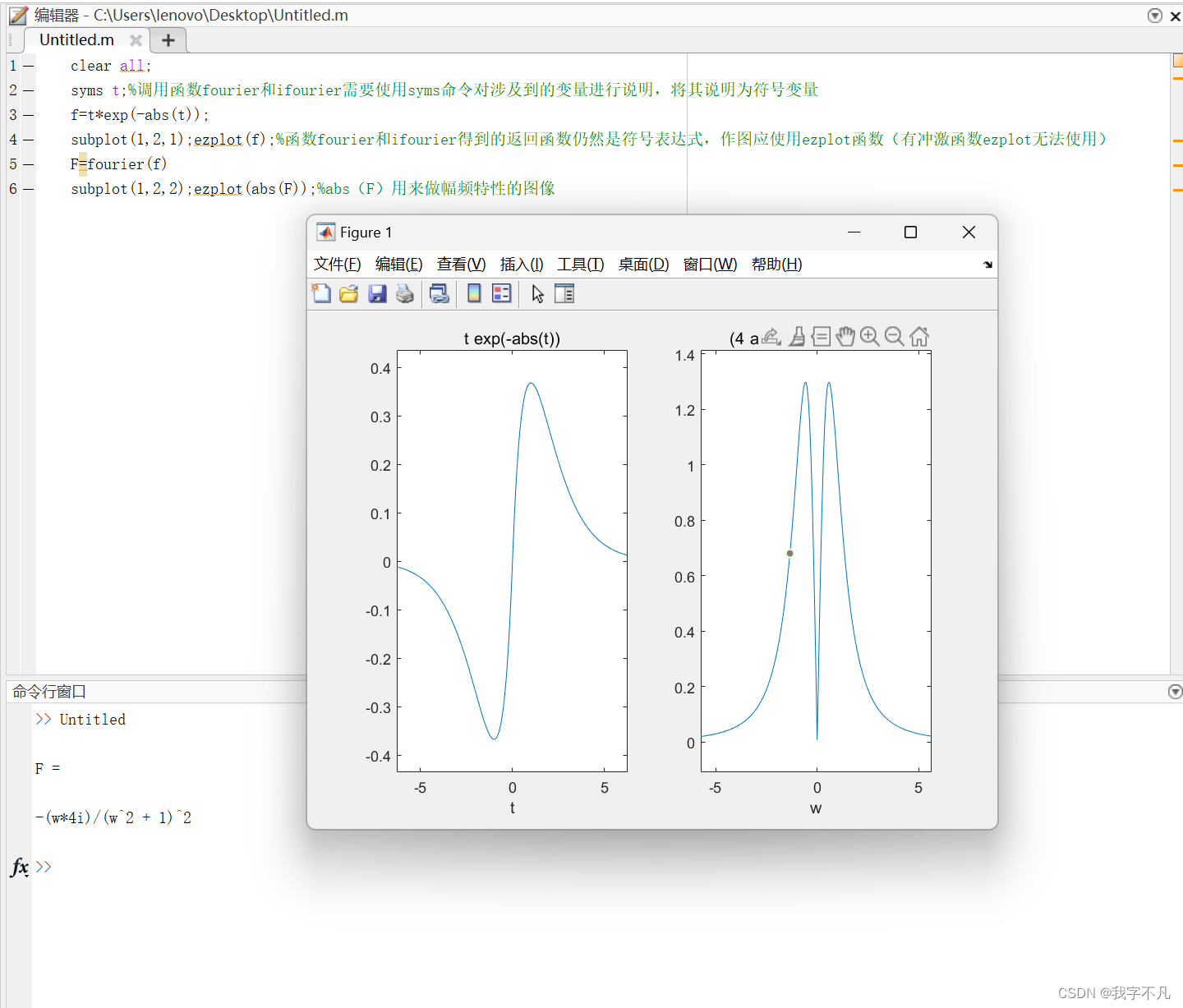

clear all;
syms t w;%在反变换中涉及到了t和w两个变量，都需要符号化
F=pi*exp(-abs(w));
subplot(1,2,1);ezplot(abs(F));%频谱图
f=ifourier(F,t)%ifourier默认返回是关于x的函数，这里指定为返回t的函数
subplot(1,2,2);ezplot(f);%时域图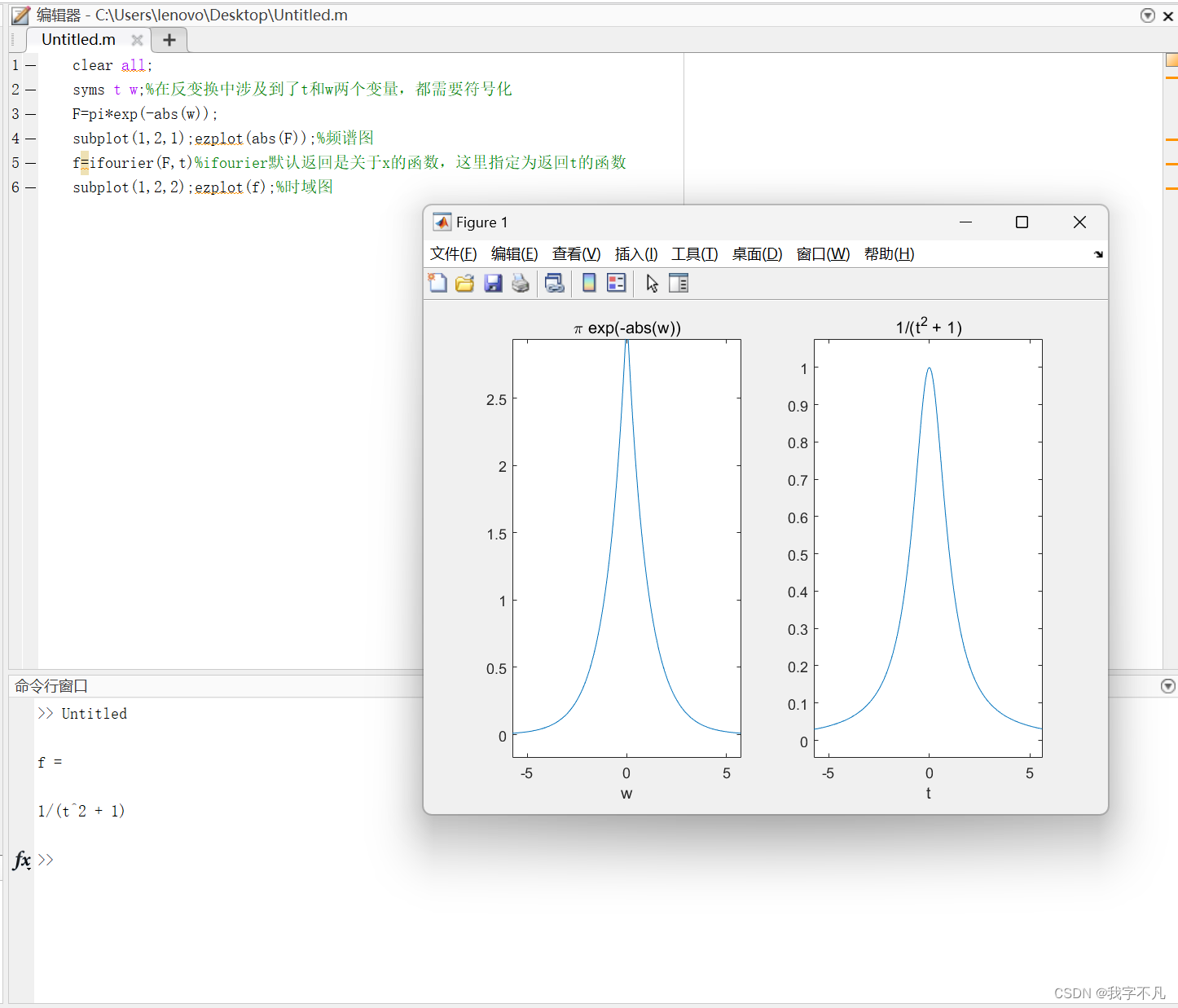

此题中是周期信号，不可积分，所以无法使用傅里叶变换，所以采用傅里叶级数进行求解

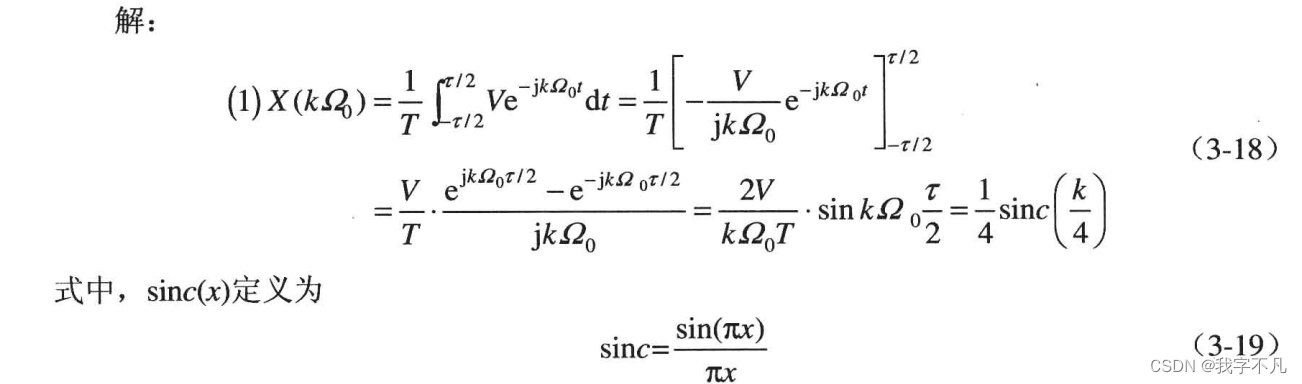
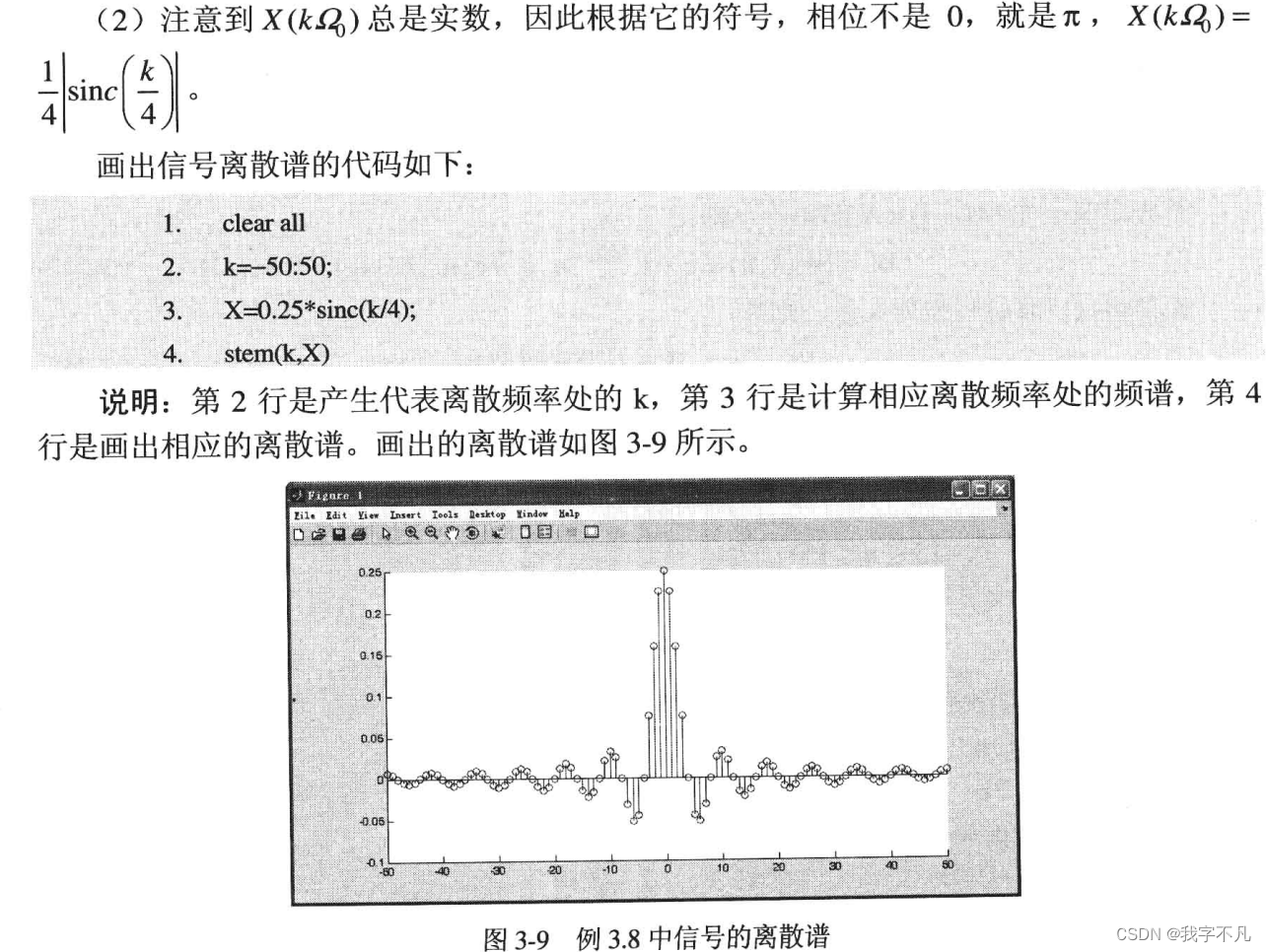
这题中我们是使用手动积分算出傅里叶级数的表达式后直接对表达式进行画图的，个人理解是因为无穷长的信号在matlab中表示较为复杂，所以反而是手动求解更快。

三、离散时间信号的傅里叶变换

clear all;
w=-1:0.001:1;%产生数字频率的范围，这里的单位长度是pi，所以只计算了[-pi,pi]范围内的DTFT
n=0:20;%离散序列的时间范围，0<n<20;
h(n+1)=1;%构造信号h(n)=1，这里n+1的理由是matlab数组都是从1开始计算的，数组索引必须为正整数或逻辑值。
x=h.*exp(j*pi*n/4);%构造信号x(n);
Hjw=h*(exp(-j*pi).^(n'*w));%dtft公式，这里n'*w是利用数字频率和时间范围构造了一个矩阵，之后将矩阵与-j*pi
%相乘后进行exp运算，最后将表达式与数字序列相乘，得到数字序列的DTFT值
Xjw=x*(exp(-j*pi).^(n'*w));
subplot(2,2,1);plot(w,abs(Hjw));
title('H');xlabel('pi弧度（w）');ylabel('振幅')
subplot(2,2,2);plot(w,angle(Hjw/pi));%用angle绘制相位图，除以pi是因为以pi弧度为单位的
title('H');xlabel('pi弧度（w）');ylabel('相位')
subplot(2,2,3);plot(w,abs(Xjw));
title('H');xlabel('pi弧度（w）');ylabel('振幅')
subplot(2,2,4);plot(w,angle(Xjw/pi));
title('H');xlabel('pi弧度（w）');ylabel('相位')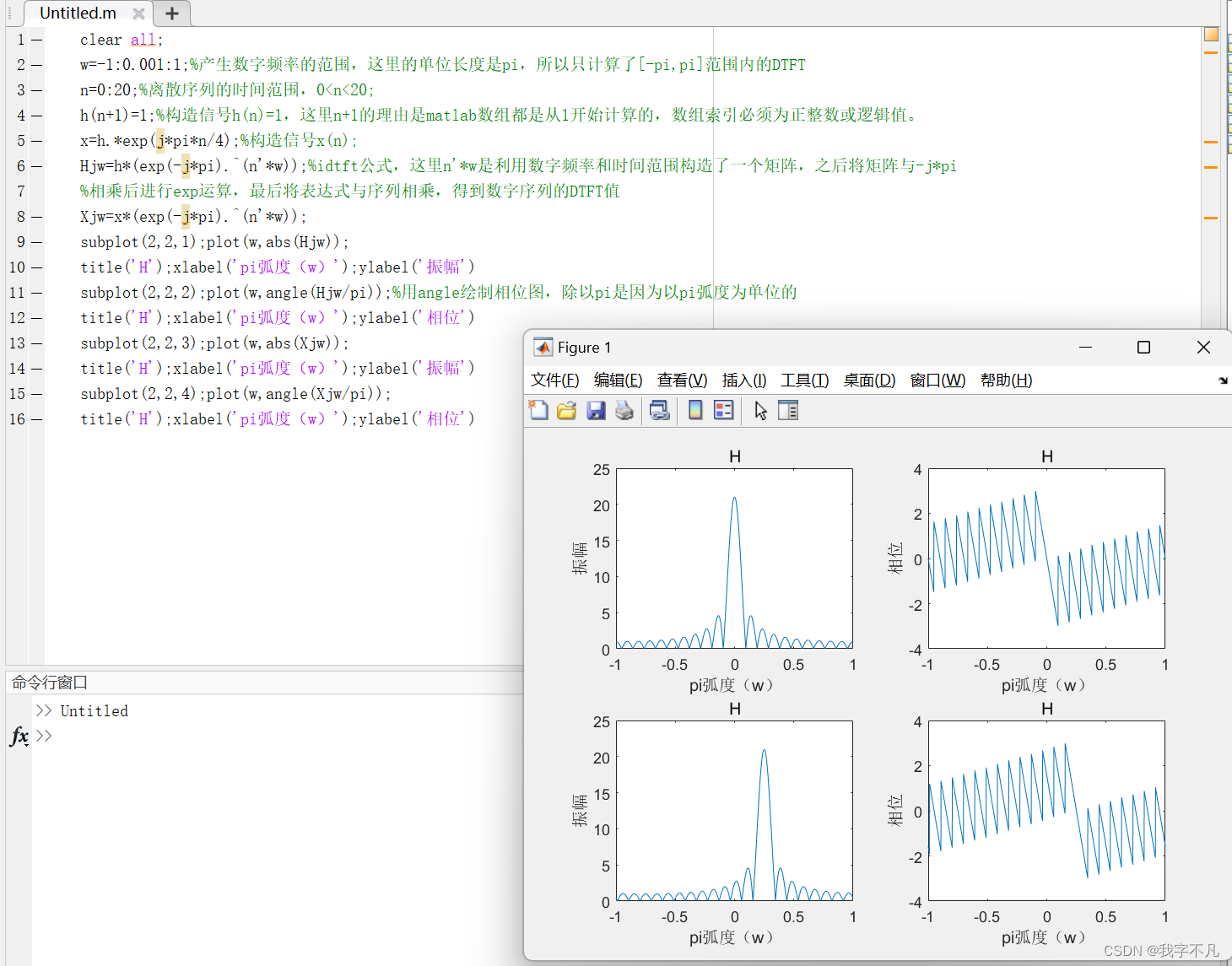

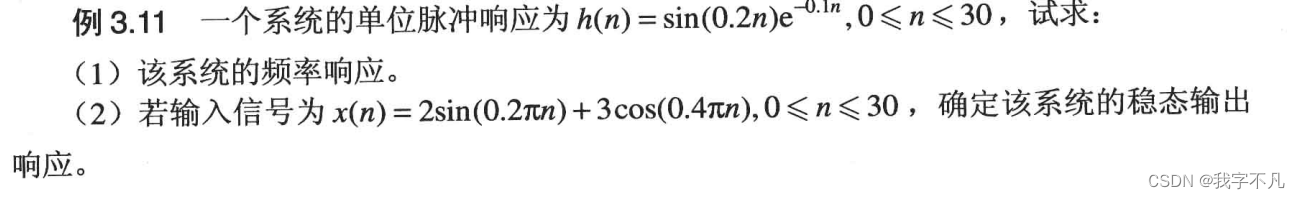
clear all;
w=-1:0.001:1;%产生数字频率的范围，这里的单位长度是pi，所以只计算了[-pi,pi]范围内的DTFT
n=0:30;%离散序列的时间范围，0<n<30;
h=sinc(0.2*n);
x=2*sin(0.2*pi*n)+3*cos(0.4*pi*n);
Hjw=h*(exp(-j*pi).^(n'*w));
Xjw=x*(exp(-j*pi).^(n'*w));
Yjw=Xjw.*Hjw;%这里是第一种方法，通过DTFT求出x和h信号的傅里叶变换然后相乘，得到了输出响应y的频域表达
n1=0:2*length(n)-2;%这里卷积之后的长度等于用于卷积的序列长度相加-1（n+n-1）
dw=0.001*pi;%确定分段求和的步长
y=(dw*Yjw*(exp(j*pi).^(w'*n1)))/(2*pi);%通过y的频域表达得到y的时域表达，需要用到IDTFT，由于IDTFT公式中用到了积分，这里使用
%分段求和代替积分，步长等于相邻频域的间隔，因为w=-1:0.001:1;，所以步长是0.001*pi。求和中和DTFT思路一致，都是用w'*n1
%两个参数构造的矩阵实现的

y1=conv(x,h);%这是第二种方法，时域卷积，第一种是频域相乘，总结来说，就是时域卷积等价于频域相乘。
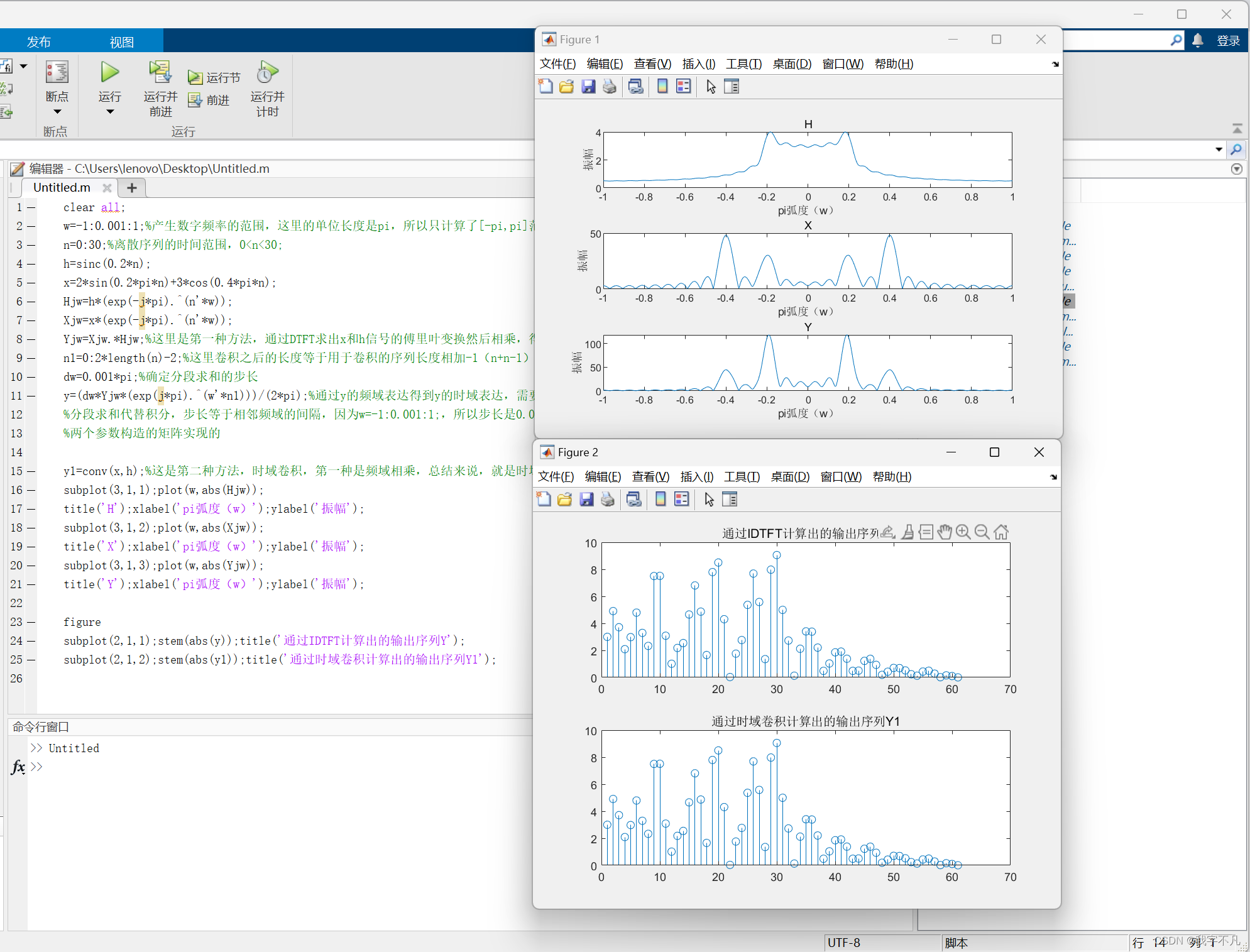
subplot(3,1,1);plot(w,abs(Hjw));
title('H');xlabel('pi弧度（w）');ylabel('振幅');
subplot(3,1,2);plot(w,abs(Xjw));
title('X');xlabel('pi弧度（w）');ylabel('振幅');
subplot(3,1,3);plot(w,abs(Yjw));
title('Y');xlabel('pi弧度（w）');ylabel('振幅');  

figure
subplot(2,1,1);stem(abs(y));title('通过IDTFT计算出的输出序列Y');
subplot(2,1,2);stem(abs(y1));title('通过时域卷积计算出的输出序列Y1');