这里写目录标题
- 什么是多状态DP
- 解决多状态DP问题应该怎么做?
- 关于多状态DP问题的几道题
- 1.按摩师
- 2.打家劫舍Ⅱ
- 3.删除并获得点数
- 4.粉刷房子
- 5.买卖股票的最佳时期含手冷冻期
- 总结

什么是多状态DP
多状态动态规划(Multi-State Dynamic Programming, Multi-State DP)问题是动态规划(DP)领域中的一个高级概念,涉及到在算法设计中引入多个状态来描述和解决复杂问题。与传统的单状态DP问题相比,多状态DP问题能够处理更多维度的状态信息,以应对更复杂的决策过程和状态转移关系。
以下是对多状态DP问题的详细介绍,包括定义、特点、常见应用场景和解决方法:
- 定义
多状态DP问题是指在动态规划算法中,引入了多个状态变量来描述一个问题的状态空间,并在这些状态之间进行转移来优化目标函数。每个状态变量通常代表了问题的一种不同的维度或特征,共同影响最终的决策过程。
简单定义:
在多状态DP问题中,我们使用一个或多个状态变量来描述问题的当前状态,并通过状态转移方程来找到从初始状态到目标状态的最优解。
- 特点
状态空间多维:与单状态DP不同,多状态DP问题中包含多个状态变量,每个状态变量可以是一个离散的值或者一个连续的范围。
状态转移复杂:状态之间的转移关系可能更加复杂,需要同时考虑多个维度的变化。
优化目标:目标通常是最小化或最大化一个函数,这个函数依赖于多个状态变量的组合。 - 常见应用场景
路径规划:如在地图上寻找从起点到终点的最短路径时,可以使用多个状态来描述不同的交通模式、时间限制等。
资源分配:如在生产计划中,考虑生产任务的时间、资源消耗、设备状态等多个因素来优化生产计划。
游戏设计:如在游戏中模拟复杂的状态变化,如角色的技能、装备状态、关卡进展等。
网络优化:如在网络流问题中,考虑多种流量限制、路由选择等因素来优化网络流量分配。 - 常见问题类型
以下是一些典型的多状态DP问题示例:
背包问题的扩展:如多维背包问题,其中不仅需要考虑物品的重量和价值,还需要考虑物品的其他特性(例如容量、数量限制等)。
序列比对:如生物信息学中的序列比对问题,涉及对比多个序列的不同状态(如基因序列的匹配和变异)。
多阶段决策问题:如多阶段投资决策,其中每个阶段的决策会影响后续阶段的状态。
解决多状态DP问题应该怎么做?
解决方法
解决多状态DP问题通常包括以下几个步骤:
- 定义状态变量:确定问题中的所有状态变量及其可能的取值范围。
- 构建状态转移方程:描述从一个状态转移到另一个状态的规则,通常包括状态之间的转移条件和代价。
- 设定初始状态和目标状态:确定动态规划的起始状态和目标状态,以及需要优化的目标函数。
- 编写DP递推公式:根据状态转移方程编写DP算法的递推公式。
- 实现DP算法:使用编程语言实现DP算法,并进行优化以提高算法的效率。
关于多状态DP问题的几道题
1.按摩师
题目链接
问题:
样例输出和输入:
这道题题意很简单一个按摩师,可以接收源源不断的预约请求,但是有一点他的预约请求不能在相邻的两天,意思就是我们看示例1,我们如果接受了1,那么就不能接受2,但是 可以接收3,3是可接受,但是不是一定要接受,最后让我们求预约的最长的时长的总和。
算法原理
状态表示:dp[i]表示到达i位置的最长预约时长。
状态转移方程 :这里我们想,到达i位置我们是不是有两种子状态,一种是预约,一种是不预约,如果预约话前一个i-1就不能预约,因为相邻的两个不能同时预约,所以我们将预约这种状态定义为f[i],将不预约这种状态定义为g[i],这里表示预约和不预约的最长预约时间。
所以这里第一种情况:当接受i位置的预约时,我们就不能接受i-1位置的预约,则f[i]可以表示为:f[i]=g[i-1]+nums[i]
第二种情况:当不接受i位置的值的时候,i-1位置可以选,可以不选,所以这里求选和不选的最大值,g[i]=max(g[i-1],f[i-1])
代码展示:
class Solution {
public:
int massage(vector<int>& nums)
{
if(nums.size()==0)
{
return 0;
}
//讨论两种情况,选或者不选
int n = nums.size();
vector<int> f(n), g(n);
//初始化
f[0] = nums[0], g[0] = 0;
for (int i = 1;i < n;i++)
{
f[i] = g[i - 1] + nums[i];
g[i] = max(g[i - 1], f[i - 1]);
}
return max(g[n - 1], f[n - 1]);
}
};
运行结果:
2.打家劫舍Ⅱ
题目链接
问题:
样例输出和输入:
这道题讲的是一个小偷,他要偷东西,但是不能偷相邻两个房间的东西,因为偷相邻两个房间的东西会触发报警器,还有一个要求就是不能同时偷头尾两个位置的东西,然后数组中的值代表房间的价值。最后让我们求可以偷到的最高价值。
算法原理:
这道题其实和打家劫舍1一样,只需要多一个判断,判断第一个位置是否偷,如果第一个位置偷,则第二个位置不能偷,如果 第一个位置不偷,则第二个位置可以偷 也可以不偷。
然后对可以偷的部分来一次打家劫舍1就可以了。
代码展示:
class Solution {
public:
int rob(vector<int>& nums)
{
int n=nums.size();
//三种情况当中偷最大的
if(n==1)
{
return nums[0];
}
if(n==2)
{
return max(nums[0],nums[1]);
}
if(n==3)
{
return max(max(nums[0],nums[1]),nums[2]);
}
//如果选第一个位置
vector<int> f1(n),g1(n);
f1[2]=nums[0]+nums[2],g1[2]=nums[0];
for(int i=3;i<n-1;i++)
{
f1[i]=g1[i-1]+nums[i];
g1[i]=max(g1[i-1],f1[i-1]);
}
vector<int> f2(n),g2(n);
f2[1]=nums[1],g2[1]=0;
for(int i=2;i<n;i++)
{
f2[i]=g2[i-1]+nums[i];
g2[i]=max(g2[i-1],f2[i-1]);
}
return max(max(f1[n-2],g1[n-2]),max(g2[n-1],f2[n-1]));
}
};
运行结果:

3.删除并获得点数
题目链接
问题:
样例输出和输入:
这道题让我们求的是最大点数,我们先看第一个例子,如果我们选了3,我们则不能选4和2,因为4和2不满足要求。如果我们选择4,我们则不能选择3但是我们可以选择2,这样最大的点数就是6
算法原理:
先对数组进行排序,升序数组利于我们跳过,然后再创建一个辅助数组,辅助数组的大小是原数组中最大的那个数加1,这个辅助数组的用途就是 存数组中的所有的数,如果 有相同的数则相加存起来,如果没有的话,则初始化为0.
状态表示:dp[i]表示i位置的当前获得的最大点数。。
状态转移方程:这里到达i位置的时候有两种情况,选或者不选,所以我们又需要两种状态来表示,这里选f[i],不选g[i],这里如果我们选第i个位置则前后位置都不能选则f[i]=g[i-1]+arr[i]如果我们不选i位置,则i-1位置可以选也可以不选,就是求选和不选的最大值:g[i]=max(g[i-1],f[i-1])。
代码展示:
class Solution {
public:
int deleteAndEarn(vector<int>& nums) {
sort(nums.begin(), nums.end());
int n = nums.size();
vector<int> arr(nums[n - 1]+1);
for (int i = 0;i < nums.size();i++)
{
arr[nums[i]] += nums[i];
}
vector<int> f(arr.size()), g(arr.size());
f[0] = arr[0], g[0] = 0;//f[0]=2,g[0]=0
for (int i = 1;i < arr.size();i++)
{
f[i] = g[i - 1] + arr[i];
g[i] = max(g[i - 1], f[i - 1]);
}
return max(g[arr.size() - 1], f[arr.size() - 1]);
}
};
运行结果:
4.粉刷房子
题目链接
问题:
样例输出和输入:
这道题首先要读懂题,这道题给出二维数组costs[i][j],i表示有多少个房子,然后j表示三种颜色,三种颜色分别是红蓝绿,但是这三种颜色 不能涂在相邻两个格子中,最后让我们求最小的花费
算法原理:
状态表示:dp[i]表示图到第i个房间的最小的花费
状态转移方程:这里由于涉及到三种颜色,这三种颜色分别是三种状态,所以这里我们开辟一个二维数组,这个二维数组的大小是n*3,0表示红色,1表示蓝色,2表示绿色。这里当我们第i个房间,这里我们先对红色进行讨论,由于第n个房间图了红色,所以我们的前一个房间就不能图红色,就只能在蓝色和绿色中选一个颜色,所以这里的最小花费应该是i-1的蓝色和绿色的最小花费中的最小的一个再加上当前位置的红色的最小花费:dp[i][0]=min(dp[i-1][1],dp[i-1][2])+costs[i][0]
其余的也一样:dp[i][1]=min(dp[i-1][0],dp[i-1][2])+costs[i][1],dp[i][2]=dp[i-1][1]+dp[i-1][0])+costs[i][2]
代码展示:
class Solution {
public:
int minCost(vector<vector<int>>& costs)
{
int m = costs.size();
int n = costs[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
dp[0][0] = costs[0][0], dp[0][1] = costs[0][1], dp[0][2] = costs[0][2];
for (int i = 1;i < m;i++)
{
dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i][0];
dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i][1];
dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i][2];
}
return min(min(dp[m - 1][0], dp[m - 1][1]), dp[m - 1][2]);
}
};
运行结果:
5.买卖股票的最佳时期含手冷冻期
题目链接
问题:
样例输出和输入:
这道题要我们求是最大的股受益,第一个示例,如果我们买入第一个股票在2的时候卖出则就不能在在3时买入,因为卖出的往后一天处于冷冻期,所以这里我们不能买入股票,冷冻期一过,我们就可以买入股票,我们在0的时候买入一支股票,然后在2的时候卖出,则最大受益就是3.
算法原理:
状态表示:dp[i]表示到达当前位置时的最大利润
状态转移方程:当我们到达i位置时,我们有三种状态,第一种状态是买入(持有股票) ,第二种状态是卖出(未持有股票),第三种状态是冷冻期(冷冻期,不能购买股票)。这三种状态我们分别用0,1,2表示,所以这里我们就可以用一个二维DP表来表示这个dp模型。
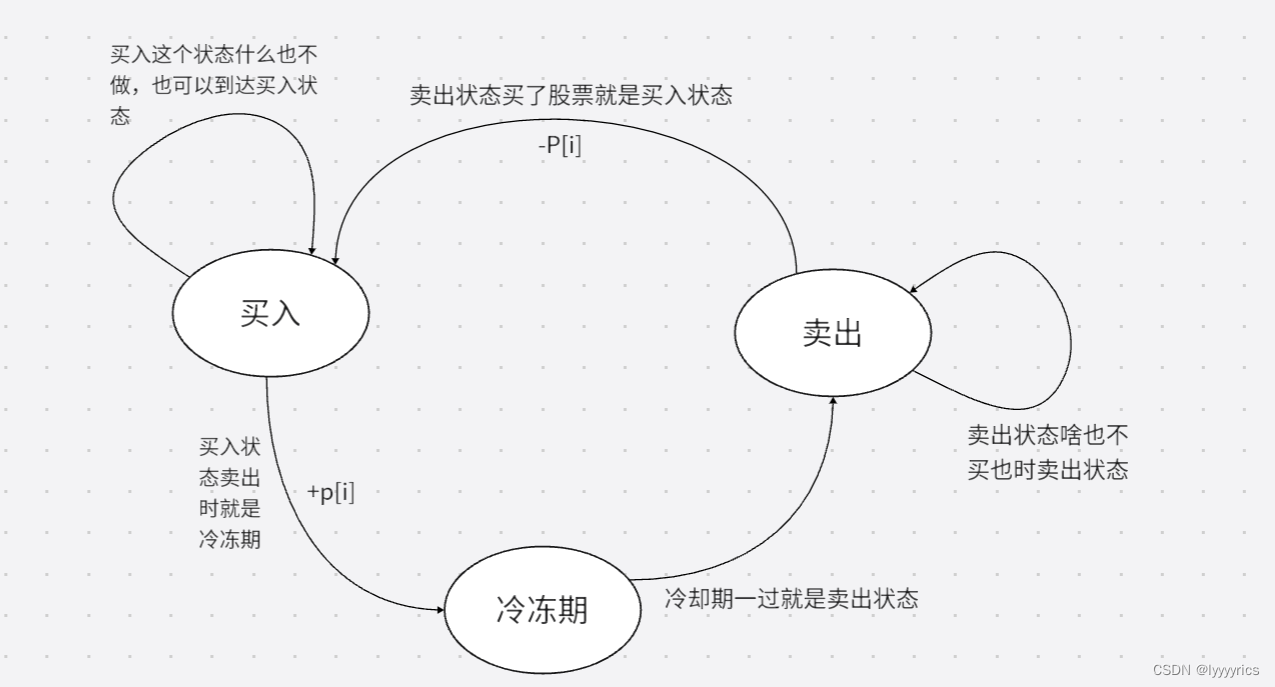
根据上图,我们可以得出简单的状态转移方程,dp[i][0]=max(dp[i-1][1]-prices[i],dp[i-1][0]]),dp[i][0]=max(dp[i-1][2],dp[i--1][1],dp[i][2]=dp[i-1][0]+prices[i]
代码展示:
class Solution {
public:
int maxProfit(vector<int>& prices)
{
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(3, 0));
//0买入状态,1可交易状态,2冷冻期
dp[0][0] = -prices[0], dp[0][1] = 0, dp[0][2] = 0;
for (int i = 1;i < n;i++)
{
dp[i][0] = max(dp[i - 1][1] - prices[i], dp[i - 1][0]);
dp[i][1] = max(dp[i - 1][2], dp[i - 1][1]);
dp[i][2] = dp[i - 1][0] + prices[i];
}
//如果最后一次交易手里还剩有股票,那么肯定不是最大的利润
return max(dp[n - 1][1], dp[n - 1][2]);
}
};
运行结果:
总结
在本文中,我们深入探讨了多状态动态规划(DP)问题的核心概念、应用场景和解法技巧。通过分析多状态DP问题的基本结构和挑战,我们不仅回顾了经典的动态规划方法,还揭示了如何在复杂的问题中引入多个状态来实现高效求解。
从具体的算法设计到实际应用案例,我们讨论了如何构建状态转移方程、优化空间复杂度以及处理状态之间的依赖关系。这些高级技巧不仅帮助我们解决了特定的多状态DP问题,也为应对未来更为复杂的算法问题奠定了坚实的基础。
多状态DP不仅是解决动态规划问题的有力工具,更是我们在算法设计中应对多维复杂性的重要思路。通过对这一领域的深入了解,我们可以更好地应对实际问题中的挑战,并在算法竞赛、数据分析等领域中取得突破性进展。
希望本文的讨论能够激发你对多状态动态规划问题的兴趣,鼓励你进一步探索这一领域的高级技巧与创新方法。算法的世界充满了无限可能,而多状态DP问题则是我们探索这片领域的一把重要钥匙。
感谢你的阅读,希望你能从中获得新的启发与收获!















![[HBM] HBM TSV (Through Silicon Via) 结构与工艺](https://img-blog.csdnimg.cn/direct/8d31fad7a28745eb81e253606f226423.png#pic_center)