目录
- 贝尔曼最优公式
- 最优 Policy
- 求解贝尔曼最优公式
- 一些影响 π ∗ \pi^* π∗ 的因素
- 如何让 π ∗ \pi^* π∗ 不 “绕弯路”
- γ \gamma γ 的影响
- reward 的影响
- 值迭代与策略迭代
- 值迭代
- 策略迭代
- 值迭代和策略迭代的具体差别
- 一个小例子
贝尔曼最优公式
作用:用于找到最优的 Policy
最优 Policy
如果存在一个 Policy π ∗ \pi^* π∗,st 对于 ∀ s \forall s ∀s 以及 ∀ π \forall \pi ∀π,都有 v π ∗ ( s ) ≥ v π ( s ) v_{\pi^*}(s) \geq v_{\pi}(s) vπ∗(s)≥vπ(s),则称为是最优 Policy
因此最优的 Policy 要保证每一个 state 上的 state value,都优于任一其他的 Policy 在该位置的 state value (Note 这里不是所有 state value 之和最大)。有以下几个问题:
- 这样的 π ∗ \pi^* π∗ 是否存在
- 这样的 π ∗ \pi^* π∗ 是否唯一
- 这样的 π ∗ \pi^* π∗ 是确定的还是有随机性
求解贝尔曼最优公式
首先回忆第一节当中的贝尔曼公式,一般形式:
v
π
(
s
)
=
∑
a
π
(
a
∣
s
)
[
∑
r
P
(
r
∣
s
,
a
)
r
+
γ
∑
s
′
P
(
s
′
∣
s
,
a
)
v
π
(
s
′
)
]
,
∀
s
\begin{aligned} v_{\pi}(s) = \sum_{a} \pi(a|s) [\sum_{r} P(r|s,a)r + \gamma \sum_{s'} P(s'|s,a) v_{\pi}(s')], \quad \forall s \end{aligned}
vπ(s)=a∑π(a∣s)[r∑P(r∣s,a)r+γs′∑P(s′∣s,a)vπ(s′)],∀s
matrix-form:
v
π
=
r
π
+
γ
P
π
v
π
v_{\pi} = r_{\pi} + \gamma P_{\pi} v_{\pi}
vπ=rπ+γPπvπ 或
v
π
=
(
I
−
γ
P
π
)
−
1
r
π
v_{\pi} = (I-\gamma P_{\pi})^{-1} r_{\pi}
vπ=(I−γPπ)−1rπ
其中
r
π
(
s
i
)
=
∑
a
π
(
a
∣
s
i
)
∑
r
P
(
r
∣
s
i
,
a
)
r
=
E
[
R
t
+
1
∣
S
t
=
s
i
]
r_{\pi}(s_i) = \sum_{a} \pi(a|s_i) \sum_{r} P(r|s_i,a)r = E[R_{t+1}|S_t=s_i]
rπ(si)=∑aπ(a∣si)∑rP(r∣si,a)r=E[Rt+1∣St=si],
P
π
(
s
i
)
=
∑
s
j
P
π
(
s
j
∣
s
i
)
P_{\pi}(s_i) = \sum_{s_j} P_{\pi}(s_j|s_i)
Pπ(si)=∑sjPπ(sj∣si)
找最优的
π
∗
\pi^*
π∗ 等价于找到最大的 State Value,即:
v
π
∗
=
max
(
(
I
−
γ
P
π
)
−
1
r
π
)
,
∀
s
,
∀
π
∈
Π
v_{\pi^*} = \max ((I-\gamma P_{\pi})^{-1} r_{\pi} ), \forall s, \forall \pi \in \Pi
vπ∗=max((I−γPπ)−1rπ),∀s,∀π∈Π
上式等价于:
v
π
∗
=
max
(
r
π
+
γ
P
π
v
π
∗
)
,
∀
s
,
∀
π
∈
Π
v_{\pi^*} = \max (r_{\pi} + \gamma P_{\pi} v_{\pi^*}), \forall s, \forall \pi \in \Pi
vπ∗=max(rπ+γPπvπ∗),∀s,∀π∈Π
后面我们将
v
π
∗
v_{\pi^*}
vπ∗ 简记为
v
∗
v^*
v∗,记
f
(
v
)
=
max
π
(
r
π
+
γ
P
π
v
)
f(v) = \max_{\pi}(r_{\pi} + \gamma P_{\pi} v)
f(v)=πmax(rπ+γPπv)
那么
v
∗
v^*
v∗ 即满足
v
∗
=
f
(
v
∗
)
v^* = f(v^*)
v∗=f(v∗) 的点。
求解最大 State Value v ∗ v^* v∗
求解上述 v ∗ = f ( v ∗ ) v^* = f(v^*) v∗=f(v∗) 需要引入 压缩映射定理:
设 ( X , d ) (X, d) (X,d) 是一个完备度量空间, T : X → X T: X \to X T:X→X 是一个压缩映射,即存在一个常数 0 ≤ k < 1 0 \leq k < 1 0≤k<1,使得对于所有的 x , y ∈ X x, y \in X x,y∈X,有:
d ( T ( x ) , T ( y ) ) ≤ k ⋅ d ( x , y ) d(T(x), T(y)) \leq k \cdot d(x, y) d(T(x),T(y))≤k⋅d(x,y)
那么 T T T 在 X X X 中有 唯一 的不动点 x ∗ x^* x∗,即 T ( x ∗ ) = x ∗ T(x^*) = x^* T(x∗)=x∗。并且,对于任意初始点 x 0 ∈ X x_0 \in X x0∈X,迭代序列 { x n } \{ x_n \} {xn} 定义为:
x n + 1 = T ( x n ) x_{n+1} = T(x_n) xn+1=T(xn)
将收敛于不动点 x ∗ x^* x∗,即:
lim n → ∞ x n = x ∗ \lim_{n \to \infty} x_n = x^* n→∞limxn=x∗
因此只要能证明存在一个度量函数
d
d
d,使得对于所以
v
1
,
v
2
v_1, v_2
v1,v2 满足:
d
(
f
(
v
1
)
,
f
(
v
2
)
)
≤
k
⋅
d
(
v
1
,
v
2
)
d(f(v_1), f(v_2)) \leq k\cdot d(v_1, v_2)
d(f(v1),f(v2))≤k⋅d(v1,v2)
就可以证明:
- 最大 State Value v ∗ v^* v∗ 存在且唯一
- 最大 State Value v ∗ v^* v∗ 可以由 v k + 1 = f ( v k ) v_{k+1}=f(v_k) vk+1=f(vk) 迭代求解
根据 v ∗ v^* v∗ 求解贪婪形式的最佳 Policy π ∗ \pi^* π∗
由于
v
π
(
s
)
=
∑
a
π
(
a
∣
s
)
q
π
(
s
,
a
)
v_{\pi}(s) = \sum_a \pi(a|s) q_{\pi}(s,a)
vπ(s)=a∑π(a∣s)qπ(s,a)
其中
q
π
(
s
,
a
)
q_{\pi}(s,a)
qπ(s,a) 是 从 state s 出发,且 take action a 的期望return,那么一定存在一个
a
∗
a^*
a∗,使得:
a
∗
(
s
)
=
arg max
a
∈
A
q
∗
(
s
,
a
)
a^*(s) = \argmax_{a \in A} q^*(s,a)
a∗(s)=a∈Aargmaxq∗(s,a)
又由于
∑
a
π
(
a
∣
s
)
=
1
\sum_{a} \pi(a|s) =1
∑aπ(a∣s)=1,因此使得
∑
a
π
(
a
∣
s
)
q
π
(
s
,
a
)
\sum_a \pi(a|s) q_{\pi}(s,a)
∑aπ(a∣s)qπ(s,a) 取得最大值的
π
∗
\pi^*
π∗ 应该形如:
π
∗
(
a
∣
s
)
=
{
1
,
a
=
a
∗
(
s
)
0
,
a
≠
a
∗
(
s
)
\pi^*(a|s) = \begin{cases} 1, \quad a = a^*(s)\\ 0, \quad a \neq a^*(s) \end{cases}
π∗(a∣s)={1,a=a∗(s)0,a=a∗(s)
上述贪婪形式的最佳 Policy
π
∗
\pi^*
π∗ 是确定形式的。根据上式,需要求解该
π
∗
\pi^*
π∗ 只需求解
a
∗
(
s
)
,
∀
s
a^*(s), \forall s
a∗(s),∀s,而
a
∗
(
s
)
=
arg max
a
∈
A
q
∗
(
s
,
a
)
a^*(s) = \argmax_{a \in A} q^*(s,a)
a∗(s)=argmaxa∈Aq∗(s,a) ,所以只需要解得所有的
q
∗
(
s
,
a
)
q^*(s,a)
q∗(s,a),根据 第一节 的内容:
q
∗
(
s
,
a
)
=
∑
r
P
(
r
∣
s
,
a
)
r
+
γ
∑
s
′
P
(
s
′
∣
s
,
a
)
v
∗
(
s
′
)
q^*(s,a) = \sum_{r} P(r|s,a)r + \gamma \sum_{s'} P(s'|s,a) v^*(s')
q∗(s,a)=r∑P(r∣s,a)r+γs′∑P(s′∣s,a)v∗(s′)
这里 v ∗ v^* v∗ 可以由 v k + 1 = f ( v k ) v_{k+1}=f(v_k) vk+1=f(vk) 迭代求解,而 P ( r ∣ s , a ) , P ( s ′ ∣ s , a ) P(r|s,a), P(s'|s,a) P(r∣s,a),P(s′∣s,a) 在前面这些章节中都认为是已知的(后面章节会讨论未知的情形)。因此 q ∗ ( s , a ) q^*(s,a) q∗(s,a) 也可以求解。由此我们完成了对贪婪形式的最佳 Policy π ∗ \pi^* π∗ 的求解。
Note: 最大 State Value
v
∗
v^*
v∗ 具有唯一性,但是达到这样的
v
∗
v^*
v∗ 的 Policy
π
∗
\pi^*
π∗ 可能并不是唯一的,例如:
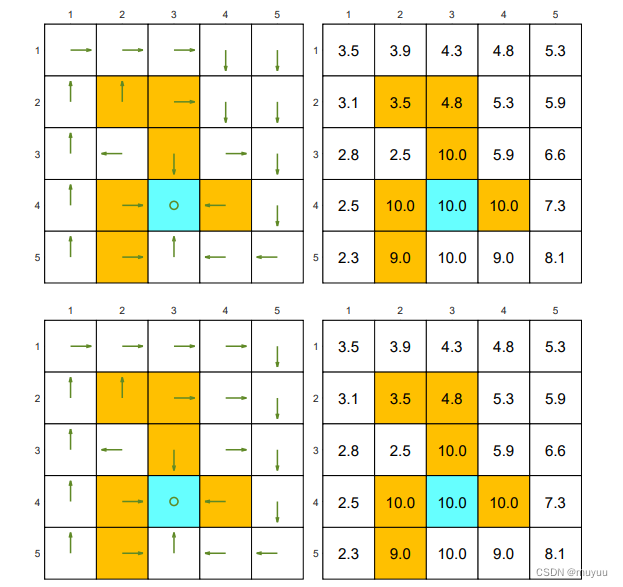
上述两个不同的 Policy, 它们的 state value 完全相同,因为在出现 diff 的部分路径上,reward总和相同
一些证明过程
为了说明 f ( v ) = max π ( r π + γ P π v ) f(v) = \max_{\pi}(r_{\pi} + \gamma P_{\pi} v) f(v)=maxπ(rπ+γPπv) 是压缩映射,只需要证明:
对任意 v 1 , v 2 v_1, v_2 v1,v2,有:
∣ ∣ f ( v 1 ) − f ( v 2 ) ∣ ∣ ∞ ≤ γ ∣ ∣ v 1 − v 2 ∣ ∣ ∞ ||f(v_1)-f(v_2)||_{\infin} \leq \gamma ||v_1 -v_2 ||_{\infin} ∣∣f(v1)−f(v2)∣∣∞≤γ∣∣v1−v2∣∣∞
其中 ∣ ∣ ⋅ ∣ ∣ ∞ ||\cdot||_{\infin} ∣∣⋅∣∣∞ 是 maximum 范数


一些影响 π ∗ \pi^* π∗ 的因素
如何让 π ∗ \pi^* π∗ 不 “绕弯路”
以下为一个简单 grid-word 的两种 Policy,显然前者优于后者,因为后者走了 “冤枉路”,本可以直接到 target state 的,却绕了弯路:
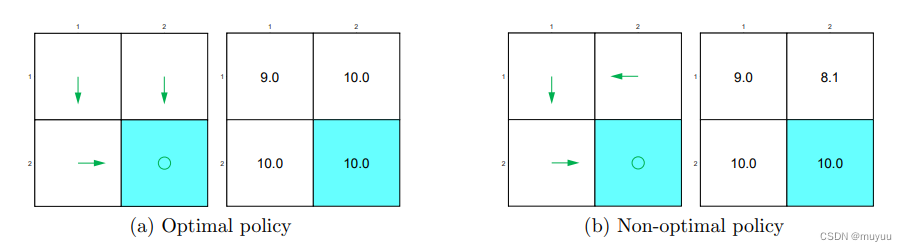
但与直观相违背的是,对于从白格子走到白格子的 action,其 reward 并不需要设为负数,而可以直接设为 0,用 discount rate
γ
\gamma
γ 来对绕弯路的行为做惩罚:
return
1
=
1
+
γ
1
+
γ
2
1
+
.
.
.
=
1
1
−
γ
return
2
=
0
+
γ
0
+
γ
2
1
+
γ
3
1
+
.
.
.
=
γ
2
1
−
γ
\begin{aligned} \text{return}_1 &= 1 + \gamma 1 + \gamma^2 1 + ... = \frac{1}{1-\gamma}\\ \text{return}_2 &= 0 + \gamma 0 + \gamma^2 1 + \gamma^3 1 + ... = \frac{\gamma^2}{1-\gamma} \end{aligned}
return1return2=1+γ1+γ21+...=1−γ1=0+γ0+γ21+γ31+...=1−γγ2
所以
return
2
\text{return}_2
return2 一定小于
return
1
\text{return}_1
return1,且
γ
\gamma
γ 越小,差距越大。一个直观的理解是:“绕弯路” 虽然不会直接产生惩罚,但是它延后了取得奖励(即到达 target state)的时间,而时间越晚,discount rate
γ
\gamma
γ 对奖励的“打折”越大,因此好的 Policy 会倾向于更快得拿到奖励
γ \gamma γ 的影响
γ
\gamma
γ 的作用除了刚刚讨论的,在 第一节 中,我们也说过,由于:
discount return
=
R
0
+
γ
R
1
+
γ
2
R
2
+
.
.
.
\begin{aligned} \text{discount return} &= R_0 + \gamma R_1 + \gamma^2 R_2 + ...\ \end{aligned}
discount return=R0+γR1+γ2R2+...
因此,当
γ
\gamma
γ更趋于0时,return更受早期的action影响,而当
γ
\gamma
γ更趋于1时,return更受后期的action的影响。可以看一些例子得到更直观的理解:
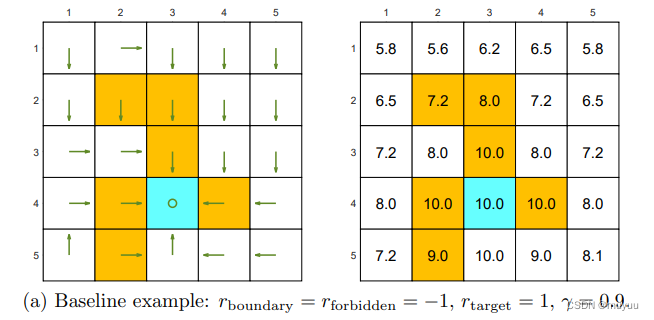
-
γ = 0.9 \gamma = 0.9 γ=0.9 时,Policy 会更受后期的action的影响,因此在接近 target state 时,为了尽快的到达,会不惜进入 forbidden state
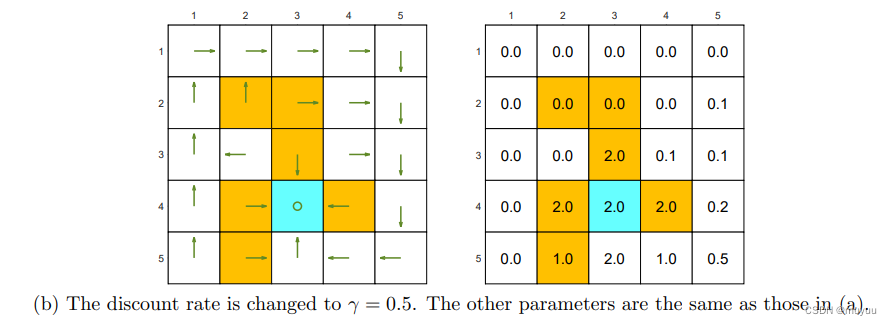
-
γ = 0.5 \gamma = 0.5 γ=0.5 时,Policy 受后期的action的影响没那么大了,相反当下立即进入 forbidden state 得到的惩罚权重更大了,因此它可能会为了避免进入 forbidden state 而绕弯路

- γ = 0 \gamma = 0 γ=0 时,Policy 会变得极端 “短时”,因为后面步骤得分的权重归零了,所以在任何 state 中,它都只倾向于走当前步所有可操作的 action 中 reward 最高的,并且不再考虑未来是否能走到 target value
reward 的影响
这里有一个也是比较直观的结论:
如果所有的 reward 都做一个线性变换: r ′ = a r + b , a > 0 r' = a r+ b, a>0 r′=ar+b,a>0
那么根据新的 reward 找到的 π ′ ∗ \pi'^* π′∗ 跟原来的 π ∗ \pi^* π∗ 相同
Proof:一个直观的理解是,由于
π
∗
(
a
∣
s
)
=
{
1
,
a
=
a
∗
(
s
)
0
,
a
≠
a
∗
(
s
)
\pi^*(a|s) = \begin{cases} 1, \quad a = a^*(s)\\ 0, \quad a \neq a^*(s) \end{cases}
π∗(a∣s)={1,a=a∗(s)0,a=a∗(s)
那么只要
a
∗
(
s
)
a^*(s)
a∗(s) 不变,
π
∗
\pi^*
π∗ 就不变。而:
a
∗
(
s
)
=
arg max
a
∈
A
q
∗
(
s
,
a
)
a^*(s) = \argmax_{a \in A} q^*(s,a)
a∗(s)=a∈Aargmaxq∗(s,a)
因此,只要这个变化不改变 reward 的 相对大小,就不会改变
a
∗
(
s
)
a^*(s)
a∗(s)。上述线性变化显然符合这个要求。
值迭代与策略迭代
值迭代
值迭代基本是上面过程的一个总结:
- 初始化一个 v 0 v_0 v0
- 迭代过程为: 已知 v k → 求解 q k ( s , a ) → π k + 1 ( a ∣ s ) = { 1 , a = a ∗ ( s ) 0 , a ≠ a ∗ ( s ) → v k + 1 = max a q k ( s , a ) 已知v_k \rightarrow 求解 q_k(s,a) \rightarrow \pi_{k+1}(a|s) = \begin{cases} 1, \quad a = a^*(s)\\ 0, \quad a \neq a^*(s) \end{cases} \rightarrow v_{k+1} = \max_a q_k(s,a) 已知vk→求解qk(s,a)→πk+1(a∣s)={1,a=a∗(s)0,a=a∗(s)→vk+1=amaxqk(s,a)
其中 q k ( s , a ) = ∑ r P ( r ∣ s , a ) r + γ ∑ s ′ P ( s ′ ∣ s , a ) v k ( s ′ ) q_k(s,a) = \sum_{r} P(r|s,a)r + \gamma \sum_{s'} P(s'|s,a) v_k(s') qk(s,a)=r∑P(r∣s,a)r+γs′∑P(s′∣s,a)vk(s′)- 当 ∣ ∣ v k + 1 − v k ∣ ∣ < ϵ ||v_{k+1} -v_k|| < \epsilon ∣∣vk+1−vk∣∣<ϵ 时,停止迭代
下面看一个具体的例子加深理解,对于如下 grid-word:
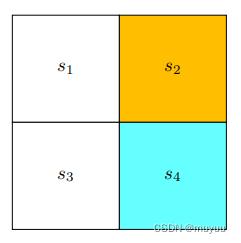
- 初始化 v 0 v_0 v0 为全零向量: v 0 ( s 1 ) = v 0 ( s 2 ) = v 0 ( s 3 ) = v 0 ( s 4 ) = 0 v_0(s_1) =v_0(s_2) = v_0(s_3) =v_0(s_4) =0 v0(s1)=v0(s2)=v0(s3)=v0(s4)=0
- 根据
q
(
s
,
a
)
q(s,a)
q(s,a) 的计算式:

q 0 ( s , a ) q_0(s,a) q0(s,a) 为:
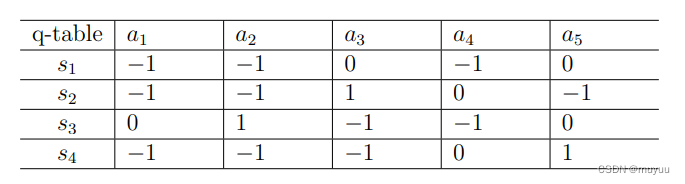
因此 π 1 \pi_1 π1 为:
π 1 ( a 5 ∣ s 1 ) = 1 , π 1 ( a 3 ∣ s 2 ) = 1 , π 1 ( a 2 ∣ s 3 ) = 1 , π 1 ( a 5 ∣ s 4 ) = 1 \pi_1(a_5|s_1) = 1, \pi_1(a_3|s_2) = 1, \pi_1(a_2|s_3) = 1, \pi_1(a_5|s_4) = 1 π1(a5∣s1)=1,π1(a3∣s2)=1,π1(a2∣s3)=1,π1(a5∣s4)=1
\qquad
Note, 这里
π
1
(
a
5
∣
s
1
)
=
1
\pi_1(a_5|s_1) = 1
π1(a5∣s1)=1 或者
π
1
(
a
3
∣
s
1
)
=
1
\pi_1(a_3|s_1) = 1
π1(a3∣s1)=1 均可,随机取一个。
v
1
v_1
v1 的值也随即可得:
v
1
(
s
1
)
=
0
,
v
1
(
s
2
)
=
1
,
v
1
(
s
3
)
=
1
,
v
1
(
s
4
)
=
1
v_1(s_1)=0, v_1(s_2)=1, v_1(s_3)=1, v_1(s_4)=1
v1(s1)=0,v1(s2)=1,v1(s3)=1,v1(s4)=1
π
1
\qquad\pi_1
π1对应的 grid-word 图为:
\qquad
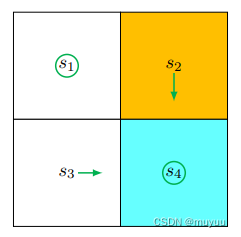
\qquad
显然这还不是最优解,
s
1
s_1
s1 的 policy 还有优化空间
- 根据上述
v
1
v_1
v1 可以求
q
1
(
s
,
a
)
q_1(s,a)
q1(s,a):

因此 π 2 \pi_2 π2 为:
π 1 ( a 3 ∣ s 1 ) = 1 , π 1 ( a 3 ∣ s 2 ) = 1 , π 1 ( a 2 ∣ s 3 ) = 1 , π 1 ( a 5 ∣ s 4 ) = 1 \pi_1(a_3|s_1) = 1, \pi_1(a_3|s_2) = 1, \pi_1(a_2|s_3) = 1, \pi_1(a_5|s_4) = 1 π1(a3∣s1)=1,π1(a3∣s2)=1,π1(a2∣s3)=1,π1(a5∣s4)=1
v 2 v_2 v2 为:
v 2 ( s 1 ) = γ , v 2 ( s 2 ) = 1 + γ , v 2 ( s 3 ) = 1 + γ , v 2 ( s 4 ) = 1 + γ v_2(s_1)=\gamma, v_2(s_2)=1+\gamma, v_2(s_3)=1+\gamma, v_2(s_4)=1+\gamma v2(s1)=γ,v2(s2)=1+γ,v2(s3)=1+γ,v2(s4)=1+γ
此时图为:
\qquad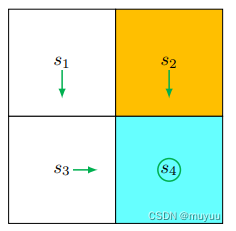
达到最优 Policy。
策略迭代
与值迭代不同,策略迭代是先从初始化策略 π 0 \pi_0 π0 开始的,迭代过程:
已知 π k → ( v π k ( 0 ) → v π k ( 1 ) → . . . → v π k ( ∞ ) = v π k ) → 求解 q π k ( s , a ) → π k + 1 = { 1 , a = a ∗ ( s ) 0 , a ≠ a ∗ ( s ) → . . . 已知 \pi_k \rightarrow (v_{\pi_k}^{(0)} \rightarrow v_{\pi_k}^{(1)} \rightarrow ... \rightarrow v_{\pi_k}^{(\infin)} = v_{\pi_k}) \rightarrow 求解 q_{\pi_k}(s,a) \rightarrow \pi_{k+1}= \begin{cases} 1, \quad a = a^*(s)\\ 0, \quad a \neq a^*(s) \end{cases} \rightarrow ... 已知πk→(vπk(0)→vπk(1)→...→vπk(∞)=vπk)→求解qπk(s,a)→πk+1={1,a=a∗(s)0,a=a∗(s)→...
上面跟值迭代相比最主要的不同是 ( v π k ( 0 ) → v π k ( 1 ) → . . . → v π k ( ∞ ) = v π k ) (v_{\pi_k}^{(0)} \rightarrow v_{\pi_k}^{(1)} \rightarrow ... \rightarrow v_{\pi_k}^{(\infin)} = v_{\pi_k}) (vπk(0)→vπk(1)→...→vπk(∞)=vπk),将其展开:
v π k ( 1 ) = r π k + γ P π k v π k ( 0 ) v π k ( 2 ) = r π k + γ P π k v π k ( 1 ) … v π k ( ∞ ) = r π k + γ P π k v π k ( ∞ ) \begin{aligned} v_{\pi_k}^{(1)} &= r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k}^{(0)}\\ v_{\pi_k}^{(2)} &= r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k}^{(1)}\\ & \dots \\ v_{\pi_k}^{(\infin)} &= r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k}^{(\infin)}\\ \end{aligned} vπk(1)vπk(2)vπk(∞)=rπk+γPπkvπk(0)=rπk+γPπkvπk(1)…=rπk+γPπkvπk(∞)
那么首先一个问题是,由于 v v v 不再是通过 v k + 1 = max π ( r π + γ P π v k ) v_{k+1} = \max_{\pi}(r_{\pi} + \gamma P_{\pi} v_k) vk+1=maxπ(rπ+γPπvk) 来求解了,那么上述策略迭代的有效性要如何保证呢? 保证上述迭代策略的有效性可以分成两个部分:
- π k + 1 \pi_{k+1} πk+1 是否总是比 π k \pi_k πk 更好
- 上述迭代能否收敛
要证明 π k + 1 \pi_{k+1} πk+1 是否总是比 π k \pi_k πk 更好,只需要证明 v π k + 1 ≥ v π k v_{\pi_{k+1}} \geq v_{\pi_k} vπk+1≥vπk 总成立
Proof: 由于
v
π
k
=
r
π
k
+
γ
P
π
k
v
π
k
v
π
k
+
1
=
r
π
k
+
1
+
γ
P
π
k
+
1
v
π
k
+
1
\begin{aligned} v_{\pi_k} &= r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k}\\ v_{\pi_{k+1}} &= r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}} v_{\pi_{k+1}} \end{aligned}
vπkvπk+1=rπk+γPπkvπk=rπk+1+γPπk+1vπk+1
由于
π
k
+
1
=
arg max
π
(
r
π
k
+
γ
P
π
k
v
π
k
)
\pi_{k+1} = \argmax_{\pi} (r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k})
πk+1=argmaxπ(rπk+γPπkvπk) 其中
v
π
k
v_{\pi_k}
vπk 是固定值, (该式总成立,因为
π
k
+
1
=
{
1
,
a
=
a
∗
(
s
)
0
,
a
≠
a
∗
(
s
)
\pi_{k+1}= \begin{cases} 1, \quad a = a^*(s)\\ 0, \quad a \neq a^*(s) \end{cases}
πk+1={1,a=a∗(s)0,a=a∗(s) 即为该式的贪婪解)
因此
r
π
k
+
1
+
γ
P
π
k
+
1
v
π
k
≥
r
π
k
+
γ
P
π
k
v
π
k
=
v
π
k
r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}} v_{\pi_k} \geq r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k} = v_{\pi_k}
rπk+1+γPπk+1vπk≥rπk+γPπkvπk=vπk
⇒
v
π
k
+
1
−
v
π
k
≥
(
r
π
k
+
1
+
γ
P
π
k
+
1
v
π
k
+
1
)
−
(
r
π
k
+
1
+
γ
P
π
k
+
1
v
π
k
)
≥
γ
P
π
k
+
1
(
v
π
k
+
1
−
v
π
k
)
\Rightarrow v_{\pi_{k+1}} - v_{\pi_k} \geq (r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}} v_{\pi_{k+1}}) - (r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}} v_{\pi_k}) \geq \gamma P_{\pi_{k+1}} (v_{\pi_{k+1}} - v_{\pi_k})
⇒vπk+1−vπk≥(rπk+1+γPπk+1vπk+1)−(rπk+1+γPπk+1vπk)≥γPπk+1(vπk+1−vπk)
⇒
v
π
k
+
1
−
v
π
k
≥
γ
P
π
k
+
1
(
v
π
k
+
1
−
v
π
k
)
≥
γ
2
P
π
k
+
1
2
(
v
π
k
+
1
−
v
π
k
)
≥
.
.
.
≥
lim
n
→
∞
γ
n
P
π
k
+
1
n
(
v
π
k
+
1
−
v
π
k
)
\Rightarrow v_{\pi_{k+1}} - v_{\pi_k} \geq \gamma P_{\pi_{k+1}} (v_{\pi_{k+1}} - v_{\pi_k}) \geq \gamma^2 P^2_{\pi_{k+1}} (v_{\pi_{k+1}} - v_{\pi_k}) \geq ... \geq \lim_{n \rightarrow \infin} \gamma^n P^n_{\pi_{k+1}} (v_{\pi_{k+1}} - v_{\pi_k})
⇒vπk+1−vπk≥γPπk+1(vπk+1−vπk)≥γ2Pπk+12(vπk+1−vπk)≥...≥n→∞limγnPπk+1n(vπk+1−vπk)
其中
0
<
γ
<
1
0 < \gamma <1
0<γ<1,因此
lim
n
→
∞
γ
n
=
0
\lim_{n \rightarrow \infin} \gamma^n =0
limn→∞γn=0;而
P
π
k
+
1
P_{\pi_{k+1}}
Pπk+1 是随机矩阵,所以
P
π
k
+
1
n
P^n_{\pi_{k+1}}
Pπk+1n 不会发散。所以
v
π
k
+
1
−
v
π
k
≥
0
v_{\pi_{k+1}} - v_{\pi_k} \geq 0
vπk+1−vπk≥0。
收敛性的证明要依赖我们上面由 压缩映射定理 得到的结论:
v k + 1 = f ( v k ) = max π ( r π + γ P π v k ) → v ∗ v_{k+1} = f(v_k) = \max_{\pi}(r_{\pi} + \gamma P_{\pi} v_k) \rightarrow v^* vk+1=f(vk)=πmax(rπ+γPπvk)→v∗
由于 v ∗ = max ( ( I − γ P π ) − 1 r π ) , ∀ s , ∀ π ∈ Π v^* = \max ((I-\gamma P_{\pi})^{-1} r_{\pi} ), \forall s, \forall \pi \in \Pi v∗=max((I−γPπ)−1rπ),∀s,∀π∈Π,因此 v π k ≤ v ∗ , ∀ k v_{\pi_k} \leq v^*, \forall k vπk≤v∗,∀k 一定成立。那么我们只需要证明存在上述由 v k + 1 = f ( v k ) v_{k+1} = f(v_k) vk+1=f(vk) 推导的 { v k } \{v_k\} {vk},使得满足: v k ≤ v π k , ∀ k v_{k} \leq v_{\pi_k} , \forall k vk≤vπk,∀k
由于 v k ≤ v π k ≤ v ∗ ,而 lim k → ∞ v k = v ∗ v_{k} \leq v_{\pi_k} \leq v^*,而 \lim_{k \rightarrow \infin} v_{k} = v^* vk≤vπk≤v∗,而k→∞limvk=v∗
因此可以证明 lim k → ∞ v π k = v ∗ \lim_{k \rightarrow \infin} v_{\pi_k} = v^* k→∞limvπk=v∗
Proof: 由于
v
0
v_0
v0 是任意初始化的,所以对任意
π
0
\pi_0
π0 总可以找到
v
0
v_0
v0 使得
v
π
0
≥
v
0
v_{\pi_0} \geq v_0
vπ0≥v0
由归纳法,只需要证明当
v
π
k
≥
v
k
v_{\pi_k} \geq v_k
vπk≥vk 时,
v
π
k
+
1
≥
v
k
+
1
v_{\pi_{k+1}} \geq v_{k+1}
vπk+1≥vk+1 成立。
v
π
k
+
1
−
v
k
+
1
=
(
r
π
k
+
1
+
γ
P
π
k
+
1
v
π
k
+
1
)
−
max
π
(
r
π
+
γ
P
π
v
k
)
≥
(
r
π
k
+
1
+
γ
P
π
k
+
1
v
π
k
+
1
)
−
max
π
(
r
π
+
γ
P
π
v
k
)
(
由上述结论
v
π
k
+
1
≥
v
k
)
=
(
r
π
k
+
1
+
γ
P
π
k
+
1
v
π
k
+
1
)
−
(
r
π
k
+
γ
P
π
k
v
k
)
(
由于
π
k
=
arg
max
π
(
r
π
+
γ
P
π
v
k
)
)
≥
(
r
π
k
+
γ
P
π
k
v
k
)
−
(
r
π
k
+
γ
P
π
k
v
k
)
(
由于
π
k
+
1
=
arg
max
π
(
r
π
+
γ
P
π
v
π
k
)
)
=
γ
P
π
k
(
v
π
k
−
v
k
)
≥
0
\begin{aligned} v_{\pi_{k+1}} - v_{k+1} &= (r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}} v_{\pi_{k+1}}) - \max_{\pi}(r_{\pi} + \gamma P_{\pi} v_{k})\\ &\geq (r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}} v_{\pi_{k+1}}) - \max_{\pi}(r_{\pi} + \gamma P_{\pi} v_{k}) \quad(\text{由上述结论} v_{\pi_{k+1}} \geq v_{k} )\\ &= (r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}} v_{\pi_{k+1}}) - (r_{\pi_{k}} + \gamma P_{\pi_{k}} v_{k}) \quad (\text{由于 } \pi_{k} = \arg\max_{\pi} (r_{\pi} + \gamma P_{\pi} v_{k}))\\ &\geq (r_{\pi_{k}} + \gamma P_{\pi_{k}} v_{k}) - (r_{\pi_{k}} + \gamma P_{\pi_{k}} v_{k})\quad (\text{由于 } \pi_{k+1} = \arg\max_{\pi} (r_{\pi} + \gamma P_{\pi} v_{\pi_{k}}))\\ &= \gamma P_{\pi_{k}} (v_{\pi_{k}} - v_{k}) \geq 0\\ \end{aligned}
vπk+1−vk+1=(rπk+1+γPπk+1vπk+1)−πmax(rπ+γPπvk)≥(rπk+1+γPπk+1vπk+1)−πmax(rπ+γPπvk)(由上述结论vπk+1≥vk)=(rπk+1+γPπk+1vπk+1)−(rπk+γPπkvk)(由于 πk=argπmax(rπ+γPπvk))≥(rπk+γPπkvk)−(rπk+γPπkvk)(由于 πk+1=argπmax(rπ+γPπvπk))=γPπk(vπk−vk)≥0
证毕。
值迭代和策略迭代的具体差别
以下是值迭代和策略迭代的对比图:

可以看到,当 v 0 v_0 v0 选取得当,两种策略的 π 1 \pi_1 π1 是相同的,但是从 π 2 \pi_2 π2 开始就不一定了,这是因为,计算 v π 1 v_{\pi_1} vπ1 过程实际是:

即 值迭代的 v 1 v_1 v1 其实就是策略迭代中的 v π 1 ( 1 ) v_{\pi_1}^{(1)} vπ1(1),所以就大的 iteration 而言,一般策略迭代会在 k k k 更小的时候收敛:
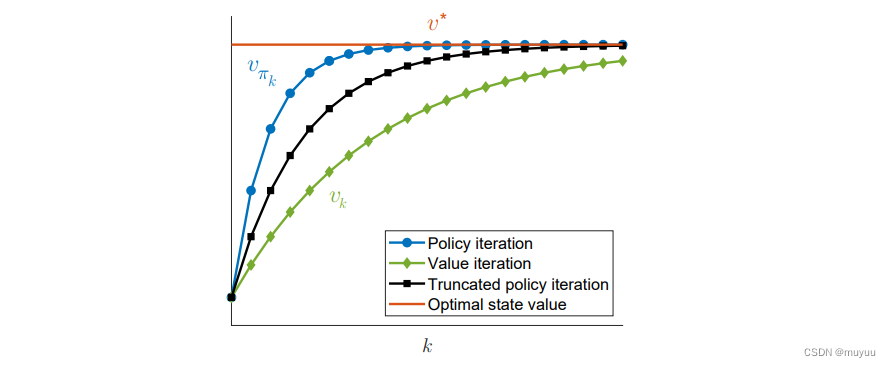
当然这不意味着策略迭代的整体计算量更小,因为它每个大的 iteration 里面,会比值迭代计算更多轮的 Value State 。
这里当介于两者之间时,称为 截断策略迭代。
一个小例子

这个小例子有一点比较有意思:可以看出 Policy 的优化往往是现从靠近 target value 的地方开始的,这个其实也很好理解,根据贝尔曼公式:
⇒
v
π
(
s
)
=
E
[
G
t
∣
S
t
=
s
]
=
E
[
R
t
+
1
+
γ
G
t
+
1
∣
S
t
=
s
]
=
E
[
R
t
+
1
∣
S
t
=
s
]
+
γ
E
[
G
t
+
1
∣
S
t
=
s
]
\begin{aligned} \Rightarrow v_{\pi}(s) &= E[G_t|S_t=s]\\ &= E[R_{t+1} + \gamma G_{t+1}|S_t=s] \\ &= E[R_{t+1}|S_t=s] + \gamma E[G_{t+1}|S_t=s] \end{aligned}
⇒vπ(s)=E[Gt∣St=s]=E[Rt+1+γGt+1∣St=s]=E[Rt+1∣St=s]+γE[Gt+1∣St=s]
其中
E
[
G
t
+
1
∣
S
t
=
s
]
E[G_{t+1}|S_t=s]
E[Gt+1∣St=s] 就是后面路径的 state value,因此要优化当前位置的 state value,一定是先优化后面的 state 的 state value,再逐渐优化远离 target value 的 state。