一个认为一切根源都是“自己不够强”的INTJ
![]() 个人主页:用哲学编程-CSDN博客
个人主页:用哲学编程-CSDN博客![]() 专栏:每日一题——举一反三
专栏:每日一题——举一反三
Python编程学习
Python内置函数
Python-3.12.0文档解读
目录
我的写法
代码点评
时间复杂度分析
空间复杂度分析
改进建议
我要更强
时间复杂度分析
空间复杂度分析
哲学和编程思想
预计算和缓存(Caching):
分治法(Divide and Conquer):
优化和效率:
迭代和递归:
抽象和模块化:
举一反三
题目链接:https://pintia.cn/problem-sets/994805342720868352/exam/problems/type/7?problemSetProblemId=994805415005503488&page=0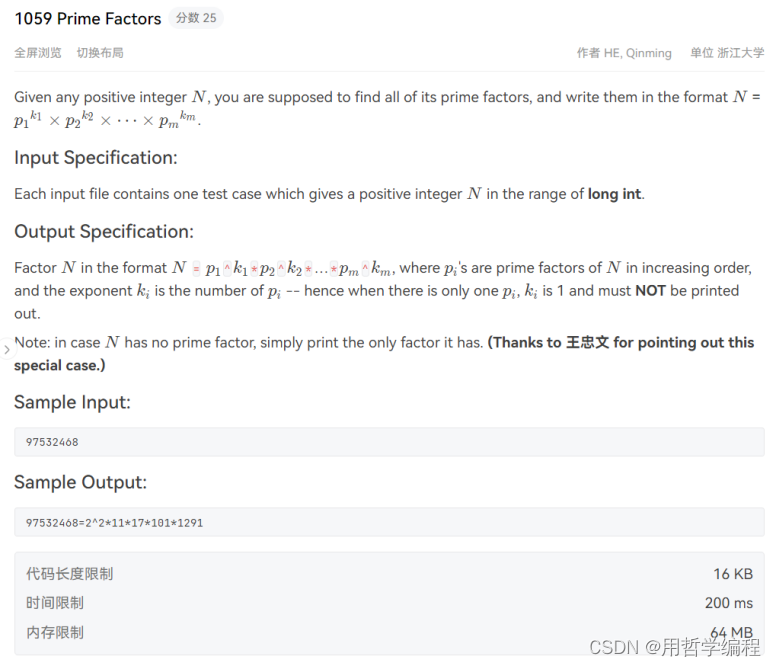
我的写法
import math # 导入数学模块,用于数学运算
N = int(input()) # 读取用户输入的整数
tmp = N # 保存原始的N值,用于输出
# 定义一个函数来检查一个数是否为质数
def is_prime(num):
if num <= 1:
return False # 小于等于1的数不是质数
if num <= 3:
return True # 2和3是质数
if num % 2 == 0 or num % 3 == 0:
return False # 能被2或3整除的数不是质数
for i in range(5, int(math.sqrt(num)) + 1, 6):
if num % i == 0 or num % (i + 2) == 0:
return False # 能被5或其后的奇数整除的数不是质数
return True # 如果通过了所有检查,则是质数
output = {} # 创建一个空字典,用于存储质因数分解的结果
# 如果N是1或者N是质数,直接输出结果并退出程序
if N == 1 or is_prime(N):
print(f"{N}={N}")
raise SystemExit(0)
# 开始质因数分解
i = 2
while i <= N:
if N % i == 0 and is_prime(i): # 如果i是N的因数且是质数
N //= i # 将N除以i
if i not in output:
output[i] = 1 # 如果i不在字典中,添加i并设置其值为1
else:
output[i] += 1 # 如果i已在字典中,增加其值
i -= 1 # 减少i的值,因为下一个循环会自动增加1
i += 1 # 增加i的值,尝试下一个可能的因数
# 输出质因数分解的结果
print(f"{tmp}=", end='')
i = 0
for k, v in output.items():
if i != 0:
print('*', end='') # 如果不是第一个质因数,输出乘号
print(k, end='') # 输出质因数
if v > 1:
print(f"^{v}", end='') # 如果质因数的指数大于1,输出指数
i += 1
代码点评
这段代码实现了对用户输入的整数进行质因数分解的功能。下面是对代码的点评:
- 功能实现:代码成功实现了质因数分解的基本功能,能够正确处理输入并输出分解结果。
- 质数检测:is_prime函数使用了优化的算法来检测质数,通过只检查到平方根的范围内,并且跳过偶数,有效地减少了不必要的计算。
- 质因数分解:使用了一个循环来找到质因数,并在找到后更新N的值。这种方法是正确的,但在性能优化方面还有改进空间。
- 输出格式:输出的格式清晰,使用了字典来存储每个质因数及其指数,便于输出和理解。
时间复杂度分析
- 质数检测:is_prime函数的时间复杂度在最坏情况下是O(sqrt(n)),因为只需要检查到n的平方根。
- 质因数分解:主循环的时间复杂度取决于找到所有质因数所需的时间。在最坏情况下,每个数都需要被检查到其平方根,因此总的时间复杂度是O(n^1.5)。然而,实际上,由于每次找到一个质因数后N的值会减小,实际的时间复杂度通常会低于这个值。
空间复杂度分析
- 存储质因数:使用了一个字典output来存储每个质因数及其出现的次数。在最坏情况下,如果N是一个大质数,字典的大小将等于N的位数,因此空间复杂度是O(log n)。在实际情况下,由于质因数通常远小于N,空间复杂度会更低。
改进建议
- 优化质因数分解:可以考虑使用更高效的算法来分解质因数,例如使用埃拉托斯特尼筛法预处理质数列表,或者使用更高效的质因数分解算法。
- 提前退出循环:在找到所有质因数后,可以提前退出循环,减少不必要的迭代。
- 代码风格:可以进一步优化代码的可读性和风格,例如添加更多的注释,使用更有意义的变量名等。
总体来说,这段代码是一个有效的质因数分解实现,但在性能和代码风格方面还有改进的空间。
我要更强
- 预处理质数列表:通过预先计算并存储一定范围内的质数,可以避免在每次调用is_prime时重复计算。
- 使用更高效的质因数分解算法:例如Pollard's rho算法或试除法优化。
- 优化循环:在找到所有质因数后提前退出循环。
下面是一个优化后的代码示例,使用了预处理质数列表的方法:
import math
# 预处理质数列表
def generate_primes(limit):
primes = []
sieve = [True] * (limit + 1)
for num in range(2, int(math.sqrt(limit)) + 1):
if sieve[num]:
primes.append(num)
for multiple in range(num * num, limit + 1, num):
sieve[multiple] = False
for num in range(int(math.sqrt(limit)) + 1, limit + 1):
if sieve[num]:
primes.append(num)
return primes
# 使用预处理的质数列表进行质因数分解
def prime_factorization(N, primes):
output = {}
for prime in primes:
if prime > N:
break
while N % prime == 0:
N //= prime
output[prime] = output.get(prime, 0) + 1
if N > 1:
output[N] = 1
return output
# 主函数
def main():
N = int(input())
primes = generate_primes(int(math.sqrt(N)) + 1)
factors = prime_factorization(N, primes)
print(f"{N}=", end='')
for factor, count in factors.items():
if count > 1:
print(f"{factor}^{count}", end='')
else:
print(f"{factor}", end='')
if factor != list(factors.keys())[-1]:
print('*', end='')
print()
if __name__ == "__main__":
main()时间复杂度分析
- 预处理质数列表:使用埃拉托斯特尼筛法,时间复杂度为O(n log(log n)),其中n是预处理的上限。
- 质因数分解:对于每个质数,我们进行一次除法操作,直到不能再被整除。在最坏情况下,这需要O(log n)的时间复杂度。
空间复杂度分析
- 存储质数列表:需要存储所有小于等于sqrt(N)的质数,空间复杂度为O(sqrt(N))。
- 存储质因数分解结果:字典output存储每个质因数及其指数,空间复杂度为O(log N)。
通过这些优化,减少了不必要的计算,并提高了代码的效率。
哲学和编程思想
这些优化方法体现了以下哲学和编程思想:
-
预计算和缓存(Caching):
- 哲学思想:这是一种“前瞻性”的思维方式,即在问题出现之前就预先准备好解决方案。在哲学上,这类似于“预防胜于治疗”的原则。
- 编程思想:在编程中,预计算和缓存是一种常见的技术,用于存储昂贵的计算结果,以便在需要时快速检索,而不是重新计算。这可以显著提高程序的效率。
-
分治法(Divide and Conquer):
- 哲学思想:分治法是一种将复杂问题分解为更小、更易于管理的部分,然后分别解决这些部分的策略。这种思想在许多哲学体系中都有体现,如“整体大于部分之和”。
- 编程思想:在编程中,分治法是一种重要的算法设计策略,用于解决递归问题,如排序算法(快速排序、归并排序)和搜索算法(二分搜索)。
-
优化和效率:
- 哲学思想:追求效率和优化是人类行为的一个基本原则,反映了“时间就是金钱”和“资源有限,需求无限”的观念。
- 编程思想:在编程中,优化意味着寻找更有效的方法来解决问题,减少资源消耗(如CPU时间、内存使用)。这通常涉及到算法分析和选择最佳的数据结构。
-
迭代和递归:
- 哲学思想:迭代和递归反映了“循环”和“重复”的概念,这在许多哲学体系中都有体现,如佛教的“轮回”和西方哲学的“永恒回归”。
- 编程思想:迭代是通过循环结构重复执行一组指令,而递归是通过函数调用自身来解决问题。这两种方法都是编程中解决重复性问题的基本技术。
-
抽象和模块化:
- 哲学思想:抽象是一种忽略细节、关注本质特征的思维方式,而模块化则是将复杂系统分解为独立、可管理的模块。这些思想在哲学中与“简化复杂性”和“关注本质”有关。
- 编程思想:在编程中,抽象和模块化是设计清晰、可维护代码的关键。通过定义抽象数据类型和模块化代码,可以提高代码的可读性和可重用性。
通过这些哲学和编程思想的应用,可以设计出更高效、更易于理解和维护的代码。
举一反三
根据上述哲学和编程思想,以下是一些技巧和策略,可以帮助你在编程和问题解决中举一反三:
- 预计算和缓存技巧:
- 在处理重复性查询或计算时,考虑使用缓存来存储结果。例如,如果你正在编写一个Web应用程序,并且某些数据查询非常耗时,可以考虑将查询结果缓存起来,以便后续请求可以快速检索。
- 对于经常使用的函数或方法,如果它们的输出不随输入变化,可以考虑将结果存储在查找表中,以便快速访问。
- 分治法应用:
- 当面对复杂问题时,尝试将其分解为更小的子问题。例如,在处理大数据集时,可以将数据集分割成小块,然后并行处理这些小块。
- 在设计算法时,考虑是否可以通过递归或迭代的方式来解决问题。例如,排序算法(如快速排序)和搜索算法(如二分搜索)都是分治法的典型应用。
- 优化和效率提升:
- 在编写代码之前,先考虑问题的最佳解决方案。了解不同算法的时间和空间复杂度,选择最适合当前问题的算法。
- 使用性能分析工具来识别代码中的瓶颈,并专注于优化这些部分。
- 迭代和递归思维:
- 对于循环问题,考虑是否可以使用迭代或递归来解决。例如,树或图的遍历通常可以使用递归实现。
- 在设计循环时,确保有一个明确的终止条件,以避免无限循环。
- 抽象和模块化设计:
- 在设计代码时,尽量使其模块化,每个模块负责一个特定的功能。这样可以提高代码的可读性和可维护性。
- 使用抽象数据类型(如类和接口)来隐藏实现细节,只暴露必要的接口。
- 学习和应用设计模式:
- 设计模式是解决常见问题的可重用解决方案。学习和应用设计模式可以帮助你更快地解决问题,并提高代码的质量。
- 例如,单例模式可以确保一个类只有一个实例,工厂模式可以用于创建对象而不暴露创建逻辑。
- 持续学习和实践:
- 编程和问题解决是一个不断学习和实践的过程。通过阅读书籍、参加在线课程、参与开源项目等方式,不断提升自己的技能。
- 实践是提高编程能力的关键。尝试解决不同类型的问题,并将学到的知识应用到实际项目中。
通过将这些哲学和编程思想融入到你的日常工作中,你将能够更有效地解决问题,并编写出更高质量的代码。记住,编程不仅仅是写代码,更是一种思维方式和解决问题的艺术。