以时间和空间两个维度分别理解卷积，先用文字来描述：

• 时间上，任何当前信号状态都是迄至当前所有信号状态的叠加；
• 时间上，任何当前记忆状态都是迄至当前所有记忆状态的叠加；
• 空间上，任何位置状态都是包括其自身在内的周边位置状态的叠加。

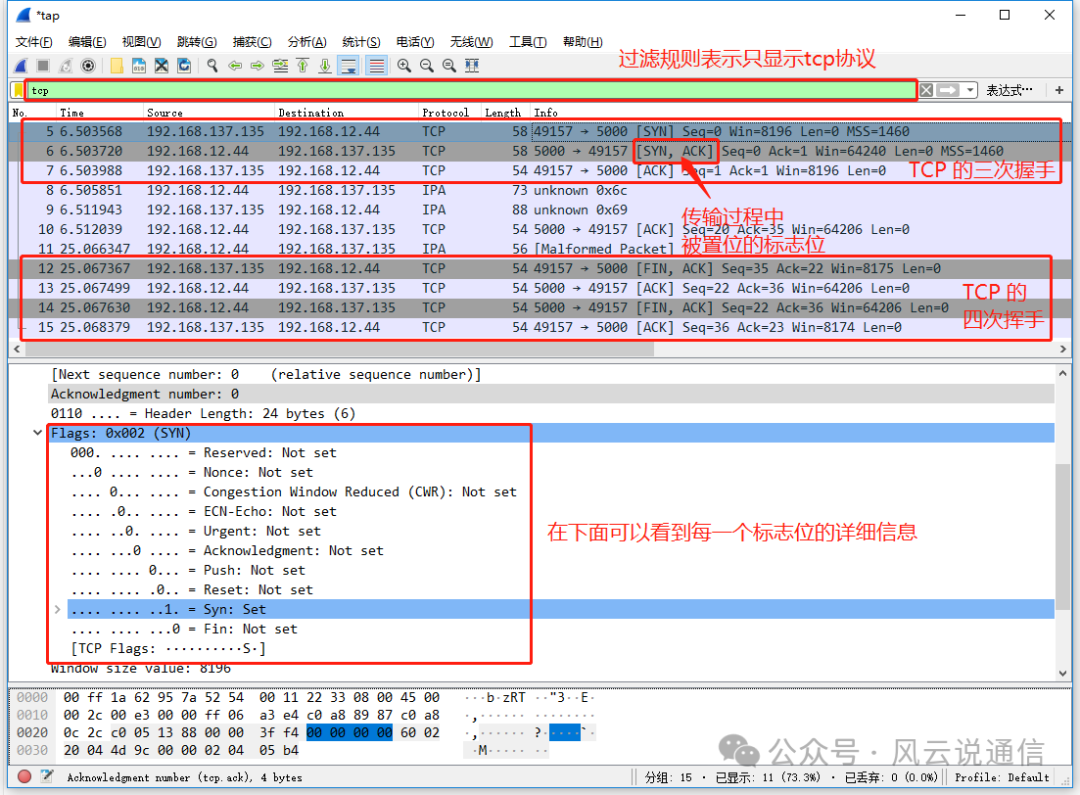
以信号 f(t) 为例，在 t 时刻的信号状态是所有 t， t -1，t - 2，t - 3，… 时刻的信号 f(t)，f(t - 1)，f(t - 2)，f(t - 3)，… 作用到当前的状态叠加，这些历史时刻的信号迄至当前分别持续了 0，1，2，3，… 个时间单位，如果 “作用力的变化” 可用 g(t) 来刻画，f(t)，f(t - 1)，f(t - 2)，f(t - 3)，… 在当前的作用力分别为 g(0)，g(1)，g(2)，g(3)，… 然后将 f(t)，f(t - 1)，f(t - 2)，f(t - 3)，… 在当前的作用力叠加起来就是了。

那么在叠加之前为什么是 f，g 相乘，即为什么是 “积”？

g(t) 解释为 “‘单位信号’ 随着时间流逝的作用力” 就高尚了。单位信号就是单位 1 的作用，即 “单位冲激”，1 个信号强度随时间流逝的作用力是 g，即 “单位冲激响应”，描述系统的特征，那么在线性系统(不解释叠加性，时不变性了)中 f 的信号强度随时间的作用力自然就是 f*g。

根据以上的段落，f(t) 的作用力是 f(t)*g(0)，f(t - 1) 的作用力是 f(t - 1)*g(1)，f(t) 的作用力是 f(t - 2)*g(2)，以此类推，f(t - r) 的作用力是 f(t - r)*g®，将所有这些加在一起就是了，连续版本如下:

${\int }_0^{t}f(t-\tau )g(\tau )d\tau$

这就好理解了，注意，我这个写法和很多教科书上是反着的，教科书上一般都是 ${\int }_0^{t}f(\tau )g(t-\tau )d\tau$，这样反而不好理解，不过有了我这个解释后也就好理解了，0 时刻的信号 f(0) 作用了 t 时间，以此类推，1，2，3，4 时刻的信号分别持续了 t - 1，t - 2，t - 3，t - 4 时间。

总结一下，如下图：

来看一个离散的例子，移动指数平均。

设时刻 t 的采样值为 $v_t$，它在整体移动指数均值中的作用按系数 $\beta$ 衰减，那么时刻 t - 1，t - 2，t - 3，… 的采样作用分别为 $v_{t-1}\cdot {\beta }^1$，$v_{t-2}\cdot {\beta }^2$，$v_{t-3}\cdot {\beta }^3$，… 那么，当前的移动指数均值就是所有这些历史采样值作用的叠加：

$A_t=(1-\beta )v_t+{\Sigma }_1^t{v}_{t-n}\cdot {\beta }^n$

这就是一个离散的卷积形式，关于移动指数平均的更多，参考 浅谈指数移动平均(ema)。

在空间域，和时间域类似，在图像处理中，往往用矩阵卷积运算 “用坐标 (u, v) 处周边坐标的特征影响坐标 (u, v) 的特征”，比如想要描边缘，g(x, y) 是一个 3 x 3 矩阵，为了加强像素差异，g(x, y) 矩阵可以写成下面这样：

$\left[\begin{array}{ccc}-1& -1& -1\\ -1& 9& -1\\ -1& -1& -1\end{array}\right]$

这个和 “当前信号状态是其周边状态的叠加” 以及 “当前移指平均是其周边采样值衰减的叠加” 异曲同工，只是时间的周边只有历史，未来尚未到来。

最后，为什么叫 “卷” 积？卷在哪里？

请看下图，一张纸两面，一面是 f(x)，另一面是 g(x)，要让 f(x) 的每一个值和 g(x) 的每一个值相乘，起码要让它们相遇，如何？只能把纸卷起来，f 和 g 才见面相乘：

浙江温州皮鞋湿，下雨进水不会胖。