那年初夏(三)
注:此部分仅为娱乐和引入用,与本文没有太大关联,可以跳过,阅读下面的正文部分。
上篇出现于:DFS(深度优先搜索)详解(概念讲解,图片辅助,例题解释,剪枝技巧)
孙翱走着,忽然想起,局长听到他一句话后,脸色有些不对劲。“难道……”,这想着,迎面撞上一个人。
“不好意思”,撞他的是一个年轻的警员,“我正在想如何完成组长布置的 统计犯罪率 最长上升子序列的任务”。
“哦?你们竟然没有工具,那么原始!我来教你,用动态规划就行,不过涉及到区间动态规划”……
那位警员,给孙翱点谢金。孙翱拿去买酒,喝完已是深夜。孙翱回到家,酒气冲头,倒头就睡,甚至忘了巡逻……
四周一下子静了下来。那弯诡异的钩月早已不知不觉的把自己藏进云层里,仿佛在恐惧着什么。惨白的光立即变成了无底的暗。天愈黑了,翻滚着的阴云带着梦魇遮住仅有的一点点光。万物都在随风发抖。
一人,站于墓前,黑暗之中,喃喃自语;一人,藏于丛中,冷风之中,紧握手枪。
丛中人,披一黑色衣,紧盯墓前人。
很久之前,我还远超于他。但,不知怎么的,他突飞猛进,将我甩到身后。我不断努力,想要反超,但总超不过。
超不过,就模仿他,成为他。
我不断模仿他,想成为他,但,不可能。学业、事业、爱情,我都不及他。无论怎么模仿,怎么学习,怎么努力。
模仿不了,就毁灭他,替代他。
丛中人缓缓举起枪。
”砰“,孙翱猛然惊醒,一身冷汗。
引入
还是那个问题:
1.动态规划是什么?
动态规划(英语:Dynamic programming,简称 DP),是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。
百度的还是那么严谨枯燥,简单来说,动态规划即:
通过将问题拆分成一个一个小问题,记录过往结果,减少重复运算。
2.什么是区间动态规划问题?
定义
区间类动态规划是线性动态规划的扩展,它在分阶段地划分问题时,与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。
性质
区间 DP 有以下特点:
合并:即将两个或多个部分进行整合,当然也可以反过来;
特征:能将问题分解为能两两合并的形式;
求解:对整个问题设最优值,枚举合并点,将问题分解为左右两个部分,最后合并两个部分的最优值得到原问题的最优值。
3.为何总是要问这种问题?
为何我总是不厌其烦地问这类问题,这种充满概念性的问题?因为,概念是实践的基础。
只有理解了概念,才能完美实践。
动态规划,懂了“通过将问题拆分成一个一个小问题,记录过往结果,减少重复运算。”这句话,就全都会有头绪。重点请看下面的:动态规划基本步骤。
区间动态规划基本 思考 步骤(划重点)
这部分,与网上其他的文章都不同,绝对通俗易懂(有点自信)
1.理解题目
2.定义dp[i]或dp[i][j]表示的是什么(通常为 题目要求的东西 的 局部最优解)
3.用递归(暴力)的思想分析每一步该怎么做
4.再就递归的思想,确认dp[i]或dp[i][j] 如何得到,由何得到
5.由上得到动态转移方程,并验证
6.思考代码如何实现(考虑细节、输入输出等)
例题精讲
都说,实践出真知,那我们就实践一下。
1.最长上升子序列
题目描述
【题意】
有n个整数组成的数列,记为: a1、a2、…、an。例如:3,18,7,14,10,12,23,41,16,24。
如果从中挑出3、18、23、24,并且保留其原有的先后顺序,就是一个长度为4的上升序列;如果挑出3、7、10、12、16、24,,并且保留其原有的先后顺序,则是长度为6的上升序列。
求出最长的上升序列的长度。
【输入格式】
第一行一个整数n(1≤n≤1000),下来n个整数。
【输出格式】
最长上升子序列的长度。
【样例输入】
10
3 18 7 14 10 12 23 41 16 24
【样例输出】
6
思路:
这是一道很经典的一维区间动态规划题。按照我上面的步骤,一步步来做吧!
题目很简洁,不用理解了。
首先,定义dp[i]或dp[i][j]表示的是什么(通常为 题目要求的东西 的 局部最优解)。既然是求一条数字串的最长上升子序列长度,那么其局部最优解就是第i个数的最长上升子序列长度,则a[i]表示包含并第i个数以此为结尾的最长上升子序列长度,因此初始化为1。
然后,用递归(暴力)的思想分析每一步该怎么做。很显然,暴力没什么方法。。。
之后,再就递归的思想,确认dp[i]或dp[i][j] 如何得到,由何得到
对于状态f[i],因为i位置前的每个位置都可能是它上一阶段的状态,所以我们需要从0到i遍历array序列,设遍历到的位置为j,那么:
如果a[i]>a[j],其能做出的决策有:
a[i]加入最长上升子序列
a[i]不加入最长上升子序列:则f[i]=1;
很显然,能加入一定加入,因为它肯定比不加入好。如果a[i]<=a[j],其能做出的决策只能是:
a[i]不加入最长上升子序列:则f[i]=1;
————————————————
参考自:最长上升子序列(LIS)问题的解决及优化_最长上升子序列优化_默归的博客-CSDN博客
在此以后,由上得到动态转移方程,并验证
因为求的是“最长”,因此,用max取大。
那么,可得:
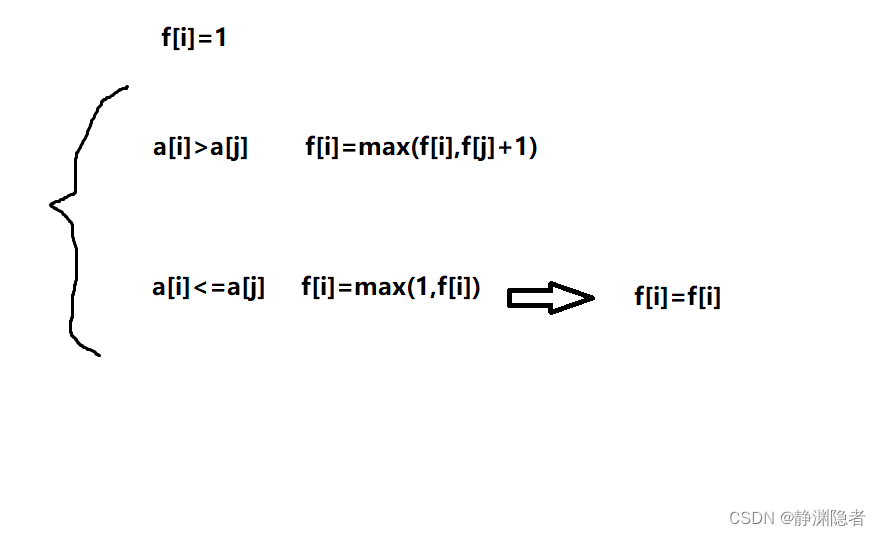
(验证就免了。。。)
最后,思考代码如何实现
第二种情况不会改变f[i],因此就免了。
这里,有一个细节有注意,a[i]表示的是包含并第i个数以此为结尾的最长上升子序列长度,而最长的未必包含最后一个数,因此不能直接输出f[n],而应比较取f[1]-f[n]的最大值,为答案。这个可在循环中完成。
代码
#include<bits/stdc++.h>
using namespace std;
int a[1005],f[1005],m,n,maxx=-1;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=i;j>=1;j--)
{
if(a[i]>a[j]) f[i]=max(f[i],f[j]+1);
}
maxx=max(maxx,f[i]);
}
cout<<maxx;//偷懒
}2.拦截导弹
题目描述
【题意】
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。
某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000的正整数,导弹数不超过1000),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
【输入格式】
输入导弹依次飞来的高度。
【输出格式】
第一行:最多能拦截的导弹数;
第二行:要拦截所有导弹最少要配备的系统数。
【输入样例】
389 207 155 300 299 170 158 65
【输出样例】
6
2
【来源】Noip1999
思路 :
这道题考的是语文!
问题抽象(这里用到了 第一步——理解题目):
1.求最多可以拦截的导弹数,就是求最长递减字串长度。
2.求最少的系统数,就是求最长不下降字串的长度。可以这样理解,假设最长的非递减字串长度为n, 那么以这最长的非递减字串的每个字符为分界点,可以将整个串分成n个小递减的小字串,这样每一发炮弹都可以拦截对应的小字串,倘若最长的非递减字串长大于n, 那么势必会有一个小字串不是递减的,则这个字串就要用不止一发子弹才能打下。
好了,理解了题目,后面算法就很简单了,不讲了(不过还要放张图,防止那些“聪明人”)!

参考:详解拦截导弹问题(动态规划)_Junieson的博客-CSDN博客
代码
#include<bits/stdc++.h>
using namespace std;
int a[1100],fup[1100],fdn[1100],n;
int main()
{
while(scanf("%d",&a[++n])!=EOF);
fup[0]=0;
for(int i=1;i<=n;i++)
{
fup[i]=1;
for(int j=i-1;j>=1;j--)
if(a[i]>a[j])
fup[i]=max(fup[i],fup[j]+1);
}
fdn[n+1]=0;
for(int i=n;i>=1;i--)
{
fdn[i]=1;
for(int j=i+1;j<=n;j++)
if(a[i]>=a[j])
fdn[i]=max(fdn[i],fdn[j]+1);
}
int s1=0,s2=0;for(int i=1;i<=n;i++) s1=max(s1,fup[i]),s2=max(s2,fdn[i]);
printf("%d\n%d\n",s2-1,s1);
return 0;
}3.护卫队
题目描述
【题意】(本题附有视频)
护卫车队在一条单行的街道前排成一队,前面河上是一座单行的桥。因为街道是一条单行道,所以任何车辆都不能超车。桥能承受一个给定的最大承载量。为了控制桥上的交通,桥两边各站一个指挥员。护卫车队被分成几个组,每组中的车辆都能同时通过该桥。当一组车队到达了桥的另一端,该端的指挥员就用电话通知另一端的指挥员,这样下一组车队才能开始通过该桥。每辆车的重量是已知的。任何一组车队的重量之和不能超过桥的最大承重量。被分在同一组的每一辆车都以其最快的速度通过该桥。一组车队通过该桥的时间是用该车队中速度最慢的车通过该桥所需的时间来表示的。问题要求计算出全部护卫车队通过该桥所需的最短时间值。
【输入格式】
第一行包含三个正整数(用空格隔开),第一个整数表示该桥所能承受的最大载重量W(用吨表示);第二个整数表示该桥的长度L(用千米表示);第三个整数表示该护卫队中车辆的总数(n<1000)。接下来的几行中,每行包含两个正整数w和v(用空格隔开),w表示该车的重量(用吨表示,车的重量在int的范围内),v表示该车过桥能达到的最快速度(用千米/小时表示)。车子的重量和速度是按车子排队等候时的顺序给出的。
【输出格式】
输出一个实数,四舍五入精确到小数点后1位,表示整个护卫车队通过该桥所需的最短时间(用分钟表示)。
【样例输入】
100 5 10
40 25
50 20
50 20
70 10
12 50
9 70
49 30
38 25
27 50
19 70
【样例输出】
75.0
思路
第一步,理解题目。在去其糟粕(几乎全是糟粕)后,可得出:
1.所有车无论怎么分组,不用考虑排序
2.任何一组车队的重量之和不能超过桥的最大承重量(边界条件)
3.一组车队通过该桥的时间是用该车队中速度最慢的车通过该桥所需的时间来表示的
第二步,定义dp[i]或dp[i][j]表示的是什么。f[i]表示1-i辆车通过桥所需的最短时间
……
后面的以后再搞(注释写得很细,自己看)。
代码
#include<bits/stdc++.h>
using namespace std;
double W,L,v[1100],w[1100],zw[1100],f[1100];
//f[i]表示第i辆车通过桥所需的最短时间
int n;
int main()
{
scanf("%lf%lf%d",&W,&L,&n);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf",&w[i],&v[i]);
v[i]/=60;//因为输出的单位要求是分钟
zw[i]=zw[i-1]+w[i];//zw[i]表示从第一辆到第i辆车的总重
}
for(int i=1;i<=n;i++)
{
double vm=f[i]=0x3f3f3f3f3f3f3f3f;//因为都应为最小值,因此初始化为最大值
for(int j=i;j>=1;j--)
{
vm=min(vm,v[j]);//寻找最慢速的车。
//vm表示车队的速度,因为最慢速的车在车队的时间中唯一有参考价值
if(zw[i]-zw[j-1]<=W)//设此车队区间为j~i,若其总重小于等于w,则可行。
{
f[i]=min(f[i],f[j-1]+L/vm);
//f[j-1]表示1~j-1辆车的最短时间,l/vm表示分j~i为车队的时间。
}
}
}
printf("%.1lf",f[n]);
}4.最大子段和
题目描述
【题意】
给定一个n个数ai,求最大子段和:连续一段和S=a[i]+a[i+1]+……+a[j](1<=i<=j<=n),求S的最大值。
【输入格式】
第一行一个整数n( 1<= n <= 10^6)。
下来给出n个整数ai(|ai|<=10^3)。
【输出格式】
一行一个整数,表示最大子段和。
【样例输入】
6
-20 11 -4 13 -5 -2
【样例输出】
20
思路
设:f[i]表示,包含a[i]并以其为结尾的最大连续和
大于0,就会越来越大;反之,小于即越来越小
那,大于0则加,小于则为a[i]自己。(一重循环,因为是连续的)
同样要注意,a[i]表示的是包含并第i个数以此为结尾的最大字段和,而最长的未必包含最后一个数,因此不能直接输出f[n],而应比较取f[1]-f[n]的最大值,为答案。这个可在循环中完成。
代码
#include<bits/stdc++.h>
using namespace std;
int n,a[1000005],f[1000005],maxx=-10005;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
{
if(f[i-1]>0) f[i]+=a[i]+f[i-1];
else f[i]=a[i];
maxx=max(maxx,f[i]);
}
printf("%d",maxx);
}最后
写文章不易,求点赞+评论(骂骂作者也不错)
谢谢!