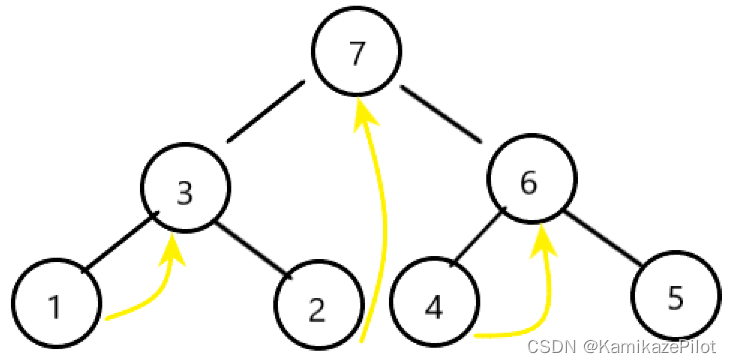
6337. 统计桌面上的不同数字

代码
后面出现的数字都是小于 n 的。
n = 1 时,答案是 1。
n > 1时:
- 第一天,n % (n - 1) == 1,n - 1会被加入
- 第二天,(n - 1) % (n - 2) == 1,n - 2 被加入
递推,一直到 2 的时候,不会加入 1,因为任何数 mod 1 都是 0,且共 1e9 天来加入数字,远大于 100,一定可以把该加入的都加入,所以共有 (n - 1) 个数字
注意特判 n 为 1 的情况
class Solution {
public int distinctIntegers(int n) {
if (n == 1) return 1;
return n - 1;
}
}
6338. 猴子碰撞的方法数

代码
每个猴子都有两种移动的方向,那么总的情况数就是 2^n
求发生碰撞的数量,太多了,我们反过来求,求碰撞的数量
正难则反
查看案例,发现不发生碰撞的情况只有两种:同时顺时针 / 逆时针
所以题目转化为了求 pow(2, n) - 2 % MOD 的形式
直接采用快速幂即可,但是因为快速幂之后要 减二,会产生负数,所以我们 减2 之后加上 mod,再进行取模
(quick_power(2, n, MOD) - 2 + MOD) % MOD
题目有些歧义,说的是 移动后 位于同一顶点才算碰撞,但是样例给定的是移动中碰撞也算了。
例如当 n = 4 时上面两个左右交换,下面两个左右交换,也不冲突,但是样例没有算。
class Solution {
public int monkeyMove(int n) {
int MOD = 1000000007;
return (quick_power(2L, n, MOD) - 2 + MOD) % MOD;
}
private static int quick_power(long a, long b, long p) {
long ans = 1;
while (b > 0) {
if ((b & 1) == 1) ans = ans * a % p;
a = a * a % p;
b >>= 1;
}
return (int) ans;
}
}
6339. 将珠子放入背包中

代码
一眼 dp,再看数据量,太大了,二维dp会超时,换方法
题目:
将序列分成 k 段,===》 切 k - 1 次,有 k - 1 个分割点,求分割点左右元素之和
求出来所有的相邻元素和,排序,求最大的 k - 1个 和 最小的 k - 1个之差即可
特殊情况::子数组中,只有最左边的一个 / 最右边的一个
但是因为所有情况都要选择这两个值,而且求的是差值,就抵消了、
所以我们只看里面的元素即可
class Solution {
public long putMarbles(int[] w, int k) {
int[] s = new int[w.length - 1];
for (int i = 0; i + 1 < w.length; i++)
s[i] = w[i] + w[i + 1];
Arrays.sort(s);
long a = 0, b = 0;
for (int i = 0; i < k - 1; i++) {
a += s[i];
b += s[s.length - i - 1];
}
return Math.abs(a - b);
}
}