一、关于`Morris`算法

简介

Morris算法是针对二叉树实现的一个遍历算法，它是一种空间复杂度为O(1)的遍历算法
通常情况下使用迭代或递归的方式遍历二叉树的空间开销都是O(N)级别的，较为理想的情况下可以做到O(logn)级别，而Morris算法通过更改节点指针指向的方式做到了它们都做不到的事情，可谓非常厉害。

主要思路

每到达一个节点cur，都查找它是否存在左孩子

如果没有左孩子，cur向右移动
如果有左孩子，找到左子树上最右侧的节点mostRight
- 如果mostRight右指针指向空，将其指向cur，然后cur向左移动
- 如果mostRight右指针指向cur，将其指向null，然后cur向右移动
cur为空时遍历停止

例：

如果有左孩子时
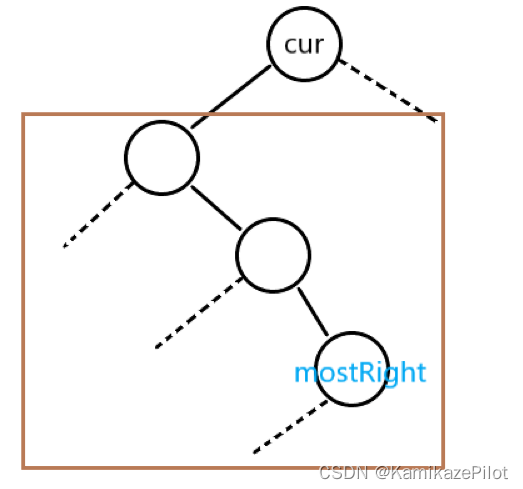
找到mostRight节点，如果是第一次到达改节点，则将其右孩子改为cur
最后cur移动到左子节点，进入下一次的循环。

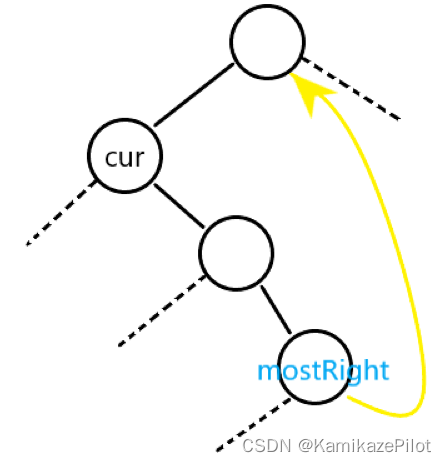
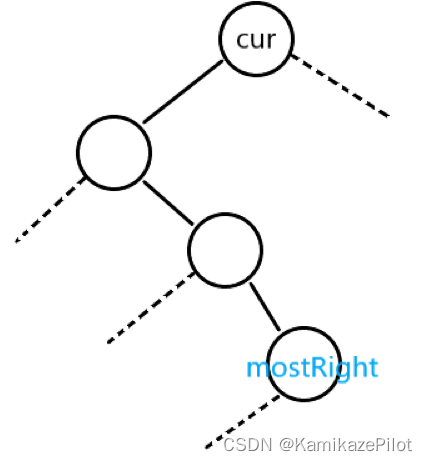
注意mostRight节点只用于判断并修改节点右孩子，真正的当前节点是cur
假设cur来到了上图中的mostRight位置，且mostRight没有左子树（为了方便说明）
则cur根据指针指向移动到黄色箭头指向的节点，并进入下一次循环
第二次来到该节点时：
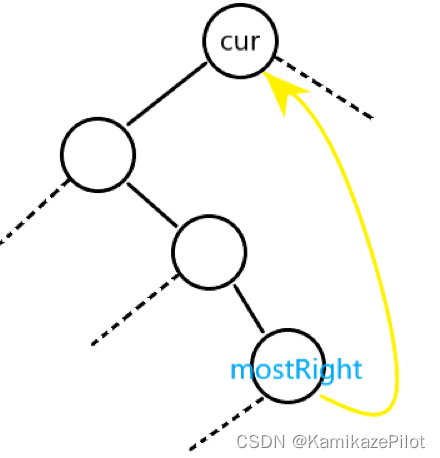
此时再次找到mostRight节点，且它的右节点与当前节点相等，那么将mostRight节点的右指针制空即可。
cur向右移动。。。

个人想法：

当你到达一个节点，并将其左子树的最右侧节点链接在当前节点上，那么当你遍历到这个节点位置时，就可以通过这个指向直接回到通常递归遍历时，需要回到的那一层；某种意义上来说，这一个操作跳过了向上查找的过程。

二、主要实现

1、基础版本

	//根节点
	Node* root;
	//标准写法
	void morris()
	{
		if (root == nullptr) return;

		Node* cur = root;
		Node* mostRight = nullptr;
		while (cur)
		{
			mostRight = cur->left;
			//查找是否存在左子树
			if (mostRight)
			{
				//查找最右节点
				while (mostRight->right && mostRight->right != cur)
					mostRight = mostRight->right;

				if (mostRight->right)	// 回到之前的节点
					mostRight->right = nullptr;
				else					//已到当前子树最右节点，向左移动
				{
					mostRight->right = cur;
					cur = cur->left;
					continue;
				}
			}
			cur = cur->right;
		}
	}

2、先序和中序遍历

通过观察整个遍历过程可知，所有有左子节点的节点一定都会到达两次

第一次是从上面遍历下来可以到达一次
第二次是从下面返回上来可以到达一次
且进入cur移动到右节点时，一定无法再次返回右节点的父亲。
根据以上性质我们可以在合适的位置选择将数据处理代码插入，先序和中序都很好实现

	//先序遍历
	vector<T>* morrisPreorder()
	{
		if (root == nullptr) return nullptr;

		vector<T>* ret = new vector<T>;
		Node* cur = root;
		Node* mostRight = nullptr;
		while (cur)
		{
			mostRight = cur->left;
			if (mostRight)
			{
				//查找最右节点
				while (mostRight->right && mostRight->right != cur)
					mostRight = mostRight->right;

				if (mostRight->right)	// 回到之前的节点
					mostRight->right = nullptr;
				else					//已到当前子树最右节点
				{
					ret->push_back(cur->value);	//第一次处理
					mostRight->right = cur;
					cur = cur->left;
					continue;
				}
			}
			else
			{
				ret->push_back(cur->value);		//第二次处理
			}
			cur = cur->right;
		}
		return ret;
	}

	//中序遍历
	vector<T>* morrisMidorder()
	{
		if (root == nullptr) return nullptr;

		vector<T>* ret = new vector<T>;

		Node* cur = root;
		Node* mostRight = nullptr;
		while (cur)
		{
			mostRight = cur->left;
			if (mostRight)
			{
				//查找最右节点
				while (mostRight->right && mostRight->right != cur)
					mostRight = mostRight->right;

				if (mostRight->right)	// 回到之前的节点
					mostRight->right = nullptr;
				else					//已到当前子树最右节点
				{
					mostRight->right = cur;
					cur = cur->left;
					continue;
				}
			}
			ret->push_back(cur->value);	//数据处理
			cur = cur->right;
		}
		return ret;
	}

3、后序遍历

课程中提到的方式是将整个左子树以右侧指针逆序，然后输出；我觉得没必要在内存上卡那么死，直接用个栈存储一下就好了

思路

在每个第二次回到的节点位置，逆序打印左子树的整条右边：

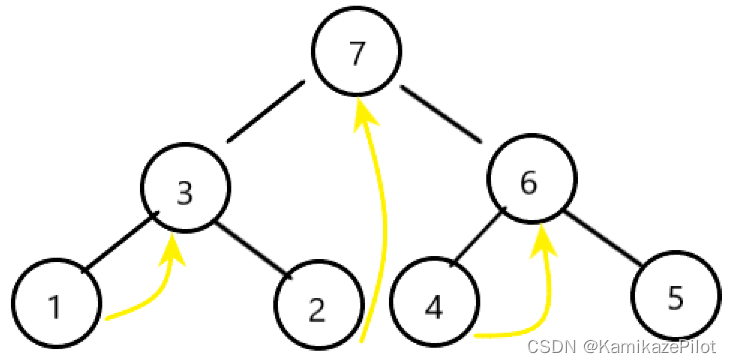
上图中，cur从头节点的遍历和输出顺序为：

7 -> 3 -> 1 -> 3(输出1) -> 2 -> 7(输出2, 3) -> 6 -> 4 -> 6(输出4) -> 5 ->
nullptr
最后再逆序输出根节点的整条右边(5, 6, 7)

	//后续遍历
	vector<T>* morrisBackorder()
	{
		if (root == nullptr) return nullptr;

		vector<T>* ret = new vector<T>;

		Node* cur = root;
		Node* mostRight = nullptr;
		while (cur)
		{
			mostRight = cur->left;
			if (mostRight)
			{
				//查找最右节点
				while (mostRight->right && mostRight->right != cur)
					mostRight = mostRight->right;

				if (mostRight->right)	// 回到之前的节点
				{
					mostRight->right = nullptr;
					func(ret, cur->left);	//插入数据
				}
				else					//已到当前子树最右节点
				{
					mostRight->right = cur;
					cur = cur->left;
					continue;
				}
			}
			cur = cur->right;
		}
		func(ret, root);
		return ret;
	}

	void func(vector<T>* vec, Node* cur)
	{
		Node* c = cur;
		stack<T> stk;
		while (c)
		{
			stk.push(c->value);
			c = c->right;
		}
		while (!stk.empty())
		{
			vec->push_back(stk.top());
			stk.pop();
		}
	}