力扣并查集

news2024/11/16 1:35:52

目录

1，路径压缩查找

323. 无向图中连通分量的数目

990. 等式方程的可满足性

200. 岛屿数量

419. 甲板上的战舰

695. 岛屿的最大面积

733. 图像渲染

1992. 找到所有的农场组

947. 移除最多的同行或同列石头

1020. 飞地的数量

547. 省份数量

827. 最大人工岛

1319. 连通网络的操作次数

1568. 使陆地分离的最少天数

1632. 矩阵转换后的秩

2，并查集退化

565. 数组嵌套

3，并查集持久化

1697. 检查边长度限制的路径是否存在（离线查询）

1724. 检查边长度限制的路径是否存在 II（在线查询）

1，路径压缩查找

323. 无向图中连通分量的数目

你有一个包含 n 个节点的图。给定一个整数 n 和一个数组 edges ，其中 edges[i] = [ai, bi] 表示图中 ai 和 bi 之间有一条边。

返回 图中已连接分量的数目 。

示例 1:

输入: n = 5, edges = [[0, 1], [1, 2], [3, 4]]
输出: 2
示例 2:

输入: n = 5, edges = [[0,1], [1,2], [2,3], [3,4]]
输出:  1
 

提示：

1 <= n <= 2000
1 <= edges.length <= 5000
edges[i].length == 2
0 <= ai <= bi < n
ai != bi
edges 中不会出现重复的边

int fa[2005];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}

class Solution {
public:
	int countComponents(int n, vector<vector<int>>& edges) {
		for (int i = 0; i < n; i++)fa[i] = i;
		for (auto &ei : edges)fa[find(ei[0])] = find(ei[1]);
		map<int, int>m;
		for (int i = 0; i < n; i++)m[find(i)] = 1;
		return m.size();
	}
};

990. 等式方程的可满足性

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一："a==b" 或 "a!=b"。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。 

示例 1：

输入：["a==b","b!=a"]
输出：false
解释：如果我们指定，a = 1 且 b = 1，那么可以满足第一个方程，但无法满足第二个方程。没有办法分配变量同时满足这两个方程。
示例 2：

输入：["b==a","a==b"]
输出：true
解释：我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。
示例 3：

输入：["a==b","b==c","a==c"]
输出：true
示例 4：

输入：["a==b","b!=c","c==a"]
输出：false
示例 5：

输入：["c==c","b==d","x!=z"]
输出：true
 

提示：

1 <= equations.length <= 500
equations[i].length == 4
equations[i][0] 和 equations[i][3] 是小写字母
equations[i][1] 要么是 '='，要么是 '!'
equations[i][2] 是 '='

int fa[26];
 
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}

class Solution {
public:
    bool equationsPossible(vector<string>& equations) {
        for (int i = 0; i <26; i++)fa[i] = i;
        for (int i = 0; i <equations.size(); i++)if(equations[i][1]=='=')fa[find(equations[i][0]-'a')]=find(equations[i][3]-'a');
        for (int i = 0; i <equations.size(); i++)if(equations[i][1]=='!' && find(equations[i][0]-'a')==find(equations[i][3]-'a'))return false;
        return true;
    }
};

200. 岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1
示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3
 

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 '0' 或 '1'

int fa[100000];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}

class Solution {
public:
	int id(int x, int y)
	{
		return x * col + y;
	}
	int numIslands(vector<vector<char>>& grid) {
		col = grid[0].size();
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			fa[id(i, j)] = id(i, j);
		for (int i = 1; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == '1' && grid[i - 1][j] == '1')if (find(id(i, j)) != find(id(i - 1, j)))fa[fa[id(i, j)]] = fa[id(i - 1, j)];
		for (int i = 0; i < grid.size(); i++)for (int j = 1; j < grid[0].size(); j++)
			if (grid[i][j] == '1' && grid[i][j - 1] == '1')if (find(id(i, j)) != find(id(i, j - 1)))fa[fa[id(i, j)]] = fa[id(i, j - 1)];
		int ans = 0;
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == '1' && fa[id(i, j)] == id(i, j))ans++;
		return ans;
	}
	int col;
};

419. 甲板上的战舰

给你一个大小为 m x n 的矩阵 board 表示甲板，其中，每个单元格可以是一艘战舰 'X' 或者是一个空位 '.' ，返回在甲板 board 上放置的 战舰 的数量。

战舰 只能水平或者垂直放置在 board 上。换句话说，战舰只能按 1 x k（1 行，k 列）或 k x 1（k 行，1 列）的形状建造，其中 k 可以是任意大小。两艘战舰之间至少有一个水平或垂直的空位分隔 （即没有相邻的战舰）。

示例 1：


输入：board = [["X",".",".","X"],[".",".",".","X"],[".",".",".","X"]]
输出：2
示例 2：

输入：board = [["."]]
输出：0
 

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 是 '.' 或 'X'
 

进阶：你可以实现一次扫描算法，并只使用 O(1) 额外空间，并且不修改 board 的值来解决这个问题吗？

这题其实是力扣 200. 岛屿数量的退化。


int fa[100000];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}
 
class Solution {
public:
	int id(int x, int y)
	{
		return x * col + y;
	}
	int countBattleships(vector<vector<char>>& grid) {
		col = grid[0].size();
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			fa[id(i, j)] = id(i, j);
		for (int i = 1; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == 'X' && grid[i - 1][j] == 'X')if (find(id(i, j)) != find(id(i - 1, j)))fa[fa[id(i, j)]] = fa[id(i - 1, j)];
		for (int i = 0; i < grid.size(); i++)for (int j = 1; j < grid[0].size(); j++)
			if (grid[i][j] == 'X' && grid[i][j - 1] == 'X')if (find(id(i, j)) != find(id(i, j - 1)))fa[fa[id(i, j)]] = fa[id(i, j - 1)];
		int ans = 0;
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == 'X' && fa[id(i, j)] == id(i, j))ans++;
		return ans;
	}
	int col;
};

695. 岛屿的最大面积

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：


输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0
 

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] 为 0 或 1

这题还是和力扣 200. 岛屿数量差不多。

int fa[100000];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}

class Solution {
public:
	int id(int x, int y)
	{
		return x * col + y;
	}
	int maxAreaOfIsland(vector<vector<int>>& grid) {
		col = grid[0].size();
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			fa[id(i, j)] = id(i, j);
		for (int i = 1; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && grid[i - 1][j] == 1)if (find(id(i, j)) != find(id(i - 1, j)))fa[fa[id(i, j)]] = fa[id(i - 1, j)];
		for (int i = 0; i < grid.size(); i++)for (int j = 1; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && grid[i][j - 1] == 1)if (find(id(i, j)) != find(id(i, j - 1)))fa[fa[id(i, j)]] = fa[id(i, j - 1)];
		map<int, int>m;
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == 1)m[find(id(i, j))]++;
		int ans = 0;
		for (auto& mi : m)ans = max(ans, mi.second);
		return ans;
	}
	int col;
};

733. 图像渲染

有一幅以 m x n 的二维整数数组表示的图画 image ，其中 image[i][j] 表示该图画的像素值大小。

你也被给予三个整数 sr ,  sc 和 newColor 。你应该从像素 image[sr][sc] 开始对图像进行 上色填充 。

为了完成 上色工作 ，从初始像素开始，记录初始坐标的 上下左右四个方向上 像素值与初始坐标相同的相连像素点，接着再记录这四个方向上符合条件的像素点与他们对应 四个方向上 像素值与初始坐标相同的相连像素点，……，重复该过程。将所有有记录的像素点的颜色值改为 newColor 。

最后返回 经过上色渲染后的图像 。

示例 1:

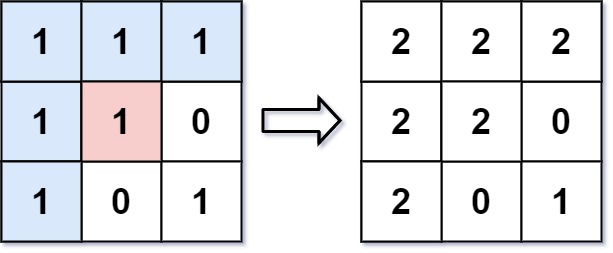
输入: image = [[1,1,1],[1,1,0],[1,0,1]]，sr = 1, sc = 1, newColor = 2
输出: [[2,2,2],[2,2,0],[2,0,1]]
解析: 在图像的正中间，(坐标(sr,sc)=(1,1)),在路径上所有符合条件的像素点的颜色都被更改成2。
注意，右下角的像素没有更改为2，因为它不是在上下左右四个方向上与初始点相连的像素点。
示例 2:

输入: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2
输出: [[2,2,2],[2,2,2]]
 

提示:

m == image.length
n == image[i].length
1 <= m, n <= 50
0 <= image[i][j], newColor < 216
0 <= sr < m
0 <= sc < n

这题还是和力扣 200. 岛屿数量差不多。

int fa[100000];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}
class Solution {
public:
	int id(int x, int y)
	{
		return x * col + y;
	}
	vector<vector<int>> floodFill(const vector<vector<int>>& grid, int sr, int sc, int color) {
		col = grid[0].size();
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			fa[id(i, j)] = id(i, j);
		for (int i = 1; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == grid[i - 1][j])if (find(id(i, j)) != find(id(i - 1, j)))fa[fa[id(i, j)]] = fa[id(i - 1, j)];
		for (int i = 0; i < grid.size(); i++)for (int j = 1; j < grid[0].size(); j++)
			if (grid[i][j] == grid[i][j - 1])if (find(id(i, j)) != find(id(i, j - 1)))fa[fa[id(i, j)]] = fa[id(i, j - 1)];
		int fid = find(id(sr, sc));
		vector<vector<int>> ans = grid;
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (find(id(i, j)) == fid)ans[i][j] = color;
		return ans;
	}
	int col;
};

1992. 找到所有的农场组

给你一个下标从 0 开始，大小为 m x n 的二进制矩阵 land ，其中 0 表示一单位的森林土地，1 表示一单位的农场土地。

为了让农场保持有序，农场土地之间以矩形的 农场组 的形式存在。每一个农场组都 仅 包含农场土地。且题目保证不会有两个农场组相邻，也就是说一个农场组中的任何一块土地都 不会 与另一个农场组的任何一块土地在四个方向上相邻。

land 可以用坐标系统表示，其中 land 左上角坐标为 (0, 0) ，右下角坐标为 (m-1, n-1) 。请你找到所有 农场组 最左上角和最右下角的坐标。一个左上角坐标为 (r1, c1) 且右下角坐标为 (r2, c2) 的 农场组 用长度为 4 的数组 [r1, c1, r2, c2] 表示。

请你返回一个二维数组，它包含若干个长度为 4 的子数组，每个子数组表示 land 中的一个 农场组 。如果没有任何农场组，请你返回一个空数组。可以以 任意顺序 返回所有农场组。

示例 1：

输入：land = [[1,0,0],[0,1,1],[0,1,1]]
输出：[[0,0,0,0],[1,1,2,2]]
解释：
第一个农场组的左上角为 land[0][0] ，右下角为 land[0][0] 。
第二个农场组的左上角为 land[1][1] ，右下角为 land[2][2] 。
示例 2：

输入：land = [[1,1],[1,1]]
输出：[[0,0,1,1]]
解释：
第一个农场组左上角为 land[0][0] ，右下角为 land[1][1] 。
示例 3：

输入：land = [[0]]
输出：[]
解释：
没有任何农场组。
 

提示：

m == land.length
n == land[i].length
1 <= m, n <= 300
land 只包含 0 和 1 。
农场组都是 矩形 的形状。

int fa[100000];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}
class Solution {
public:
	int id(int x, int y)
	{
		return x * col + y;
	}
	vector<vector<int>> findFarmland(vector<vector<int>>& grid) {
		row = grid.size();
		col = grid[0].size();
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			fa[id(i, j)] = id(i, j);
		for (int i = 1; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && grid[i][j] == grid[i - 1][j])if (find(id(i, j)) != find(id(i - 1, j)))fa[fa[id(i, j)]] = fa[id(i - 1, j)];
		for (int i = 0; i < grid.size(); i++)for (int j = 1; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && grid[i][j] == grid[i][j - 1])if (find(id(i, j)) != find(id(i, j - 1)))fa[fa[id(i, j)]] = fa[id(i, j - 1)];
		vector<vector<int>> ans;
		vector<int>v(4);
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++) {
			if (grid[i][j] != 1 || find(id(i, j)) != id(i, j))continue;
			int ti = i, tj = j;
			while (i&&grid[i - 1][j] == 1)i--;
			while (j&&grid[i][j - 1] == 1)j--;
			v[0] = i, v[1] = j;
			while (i<row-1&&grid[i + 1][j] == 1)i++;
			while (j<col-1&&grid[i][j + 1] == 1)j++;
			v[2] = i, v[3] = j;
			ans.push_back(v);
			i = ti, j = tj;
		}
		return ans;
	}
	int row;
	int col;
};

947. 移除最多的同行或同列石头

n 块石头放置在二维平面中的一些整数坐标点上。每个坐标点上最多只能有一块石头。

如果一块石头的 同行或者同列 上有其他石头存在，那么就可以移除这块石头。

给你一个长度为 n 的数组 stones ，其中 stones[i] = [xi, yi] 表示第 i 块石头的位置，返回 可以移除的石子 的最大数量。

示例 1：

输入：stones = [[0,0],[0,1],[1,0],[1,2],[2,1],[2,2]]
输出：5
解释：一种移除 5 块石头的方法如下所示：
1. 移除石头 [2,2] ，因为它和 [2,1] 同行。
2. 移除石头 [2,1] ，因为它和 [0,1] 同列。
3. 移除石头 [1,2] ，因为它和 [1,0] 同行。
4. 移除石头 [1,0] ，因为它和 [0,0] 同列。
5. 移除石头 [0,1] ，因为它和 [0,0] 同行。
石头 [0,0] 不能移除，因为它没有与另一块石头同行/列。
示例 2：

输入：stones = [[0,0],[0,2],[1,1],[2,0],[2,2]]
输出：3
解释：一种移除 3 块石头的方法如下所示：
1. 移除石头 [2,2] ，因为它和 [2,0] 同行。
2. 移除石头 [2,0] ，因为它和 [0,0] 同列。
3. 移除石头 [0,2] ，因为它和 [0,0] 同行。
石头 [0,0] 和 [1,1] 不能移除，因为它们没有与另一块石头同行/列。
示例 3：

输入：stones = [[0,0]]
输出：0
解释：[0,0] 是平面上唯一一块石头，所以不可以移除它。
 

提示：

1 <= stones.length <= 1000
0 <= xi, yi <= 104
不会有两块石头放在同一个坐标点上

int fa[100000];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}
class Solution {
public:
	int removeStones(vector<vector<int>>& grid) {
		map<int, vector<int>>mr;
		for (int i = 0; i < grid.size(); i++){
			fa[i] = i;
			mr[grid[i][0]].push_back(i);
			mr[10005 + grid[i][1]].push_back(i);
		}
		for (auto &mi : mr) {
			auto &v = mi.second;
			for (int i = 1; i < v.size(); i++)if (find(v[0]) != find(v[i]))fa[fa[v[0]]] = fa[v[i]];
		}
		int ans = grid.size();
		for (int i = 0; i < grid.size(); i++) {
			if (fa[i] == i)ans--;
		}
		return ans;
	}
};

1020. 飞地的数量

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：


输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。
示例 2：


输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 500
grid[i][j] 的值为 0 或 1

int fa[100000];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}

class Solution {
public:
	int id(int x, int y)
	{
		return x * col + y;
	}
	int atBoard(int x, int y)
	{
		if (x == 0 || x == row - 1)return true;
		if (y == 0 || y == col - 1)return true;
		return false;
	}
	int numEnclaves(vector<vector<int>>& grid) {
		row = grid.size();
		col = grid[0].size();
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			fa[id(i, j)] = id(i, j);
		for (int i = 1; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && grid[i - 1][j] == 1)if (find(id(i, j)) != find(id(i - 1, j)))fa[fa[id(i, j)]] = fa[id(i - 1, j)];
		for (int i = 0; i < grid.size(); i++)for (int j = 1; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && grid[i][j - 1] == 1)if (find(id(i, j)) != find(id(i, j - 1)))fa[fa[id(i, j)]] = fa[id(i, j - 1)];
		int ans = 0;
		map<int, int>m;
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (atBoard(i, j)&& grid[i][j] == 1)m[find(id(i, j))] = 1;
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && m[find(id(i, j))] == 0)ans++;
		return ans;
	}
	int row;
	int col;
};

547. 省份数量

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：


输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2
示例 2：


输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3
 

提示：

1 <= n <= 200
n == isConnected.length
n == isConnected[i].length
isConnected[i][j] 为 1 或 0
isConnected[i][i] == 1
isConnected[i][j] == isConnected[j][i]

int fa[100000];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}

class Solution {
public:
	int findCircleNum(vector<vector<int>>& grid) {
		for (int i = 0; i < grid.size(); i++)fa[i] = i;
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++) {
			if (grid[i][j] && find(i) != find(j))fa[fa[i]] = fa[j];
		}
		int ans = 0;
		for (int i = 0; i < grid.size(); i++)if (fa[i] == i)ans++;
		return ans;
	}
};

827. 最大人工岛

给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。

返回执行此操作后，grid 中最大的岛屿面积是多少？

岛屿 由一组上、下、左、右四个方向相连的 1 形成。

示例 1:

输入: grid = [[1, 0], [0, 1]]
输出: 3
解释: 将一格0变成1，最终连通两个小岛得到面积为 3 的岛屿。
示例 2:

输入: grid = [[1, 1], [1, 0]]
输出: 4
解释: 将一格0变成1，岛屿的面积扩大为 4。
示例 3:

输入: grid = [[1, 1], [1, 1]]
输出: 4
解释: 没有0可以让我们变成1，面积依然为 4。
 

提示：

n == grid.length
n == grid[i].length
1 <= n <= 500
grid[i][j] 为 0 或 1

int fa[250000];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}
class Solution {
public:
	int id(int x, int y)
	{
		return x * col + y;
	}
	vector<int> getNeighbor4(int k)
	{
		vector<int>ans;
		if (k >= col)ans.push_back(k - col);
		if (k < (row - 1) * col)ans.push_back(k + col);
		if (k % col)ans.push_back(k - 1);
		if (k % col < col - 1)ans.push_back(k + 1);
		return ans;
	}
	int largestIsland(vector<vector<int>>& grid) {
		row = grid.size();
		col = grid[0].size();
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			fa[id(i, j)] = id(i, j);
		for (int i = 1; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && grid[i - 1][j] == 1)if (find(id(i, j)) != find(id(i - 1, j)))fa[fa[id(i, j)]] = fa[id(i - 1, j)];
		for (int i = 0; i < grid.size(); i++)for (int j = 1; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && grid[i][j - 1] == 1)if (find(id(i, j)) != find(id(i, j - 1)))fa[fa[id(i, j)]] = fa[id(i, j - 1)];
		map<int, int>m;
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == 1)m[find(id(i, j))]++;
		int ans = 0;
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++) {
			if (grid[i][j] == 1) {
				ans = max(ans, m[find(id(i, j))]);
				continue;
			}
			vector<int> v = getNeighbor4(id(i, j));
			vector<int> v2;
			int s = 1;
			for (auto vi : v) {
				if (grid[vi / col][vi%col] == 1) {
					int k = find(vi);
					if (find(v2.begin(), v2.end(), k) == v2.end())v2.push_back(k), s += m[k];
				}
			}
			ans = max(ans, s);
		}
		return ans;
	}
	int row;
	int col;
};

1319. 连通网络的操作次数

用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b。

网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。

给你这个计算机网络的初始布线 connections，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。 

示例 1：

输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。
示例 2：

输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
输出：2
示例 3：

输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
输出：-1
解释：线缆数量不足。
示例 4：

输入：n = 5, connections = [[0,1],[0,2],[3,4],[2,3]]
输出：0
 

提示：

1 <= n <= 10^5
1 <= connections.length <= min(n*(n-1)/2, 10^5)
connections[i].length == 2
0 <= connections[i][0], connections[i][1] < n
connections[i][0] != connections[i][1]
没有重复的连接。
两台计算机不会通过多条线缆连接。

int fa[100001];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}
 
class Solution {
public:
    int makeConnected(int n, vector<vector<int>>& con) {
        if(con.size()<n-1)return -1;
        for(int i=0;i<n;i++)fa[i]=i;
        for(int i=0;i<con.size();i++)if(find(con[i][0])!=find(con[i][1]))fa[find(con[i][0])]=find(con[i][1]);
        int ans = 0;
		for (int i = 0; i < n; i++)if (fa[i] == i)ans++;
        return ans-1;
    }
};

1568. 使陆地分离的最少天数

给你一个大小为 m x n ，由若干 0 和 1 组成的二维网格 grid ，其中 1 表示陆地， 0 表示水。岛屿 由水平方向或竖直方向上相邻的 1 （陆地）连接形成。

如果 恰好只有一座岛屿 ，则认为陆地是 连通的 ；否则，陆地就是 分离的 。

一天内，可以将 任何单个 陆地单元（1）更改为水单元（0）。

返回使陆地分离的最少天数。

示例 1：

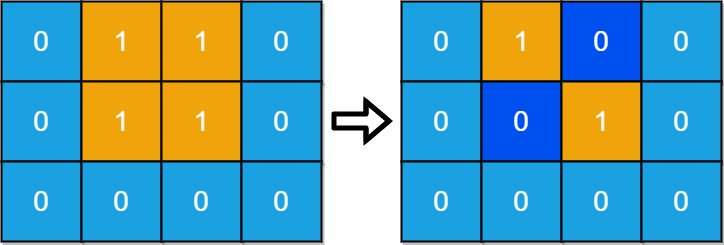
输入：grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]]
输出：2
解释：至少需要 2 天才能得到分离的陆地。
将陆地 grid[1][1] 和 grid[0][2] 更改为水，得到两个分离的岛屿。

示例 2：

输入：grid = [[1,1]]
输出：2
解释：如果网格中都是水，也认为是分离的 ([[1,1]] -> [[0,0]])，0 岛屿。

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 30
  • grid[i][j] 为 0 或 1
int fa[100000];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}

class Solution {
public:
	int id(int x, int y)
	{
		return x * col + y;
	}
	int numIslands(vector<vector<int>>& grid) {
		col = grid[0].size();
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			fa[id(i, j)] = id(i, j);
		for (int i = 1; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && grid[i - 1][j] == 1)if (find(id(i, j)) != find(id(i - 1, j)))fa[fa[id(i, j)]] = fa[id(i - 1, j)];
		for (int i = 0; i < grid.size(); i++)for (int j = 1; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && grid[i][j - 1] == 1)if (find(id(i, j)) != find(id(i, j - 1)))fa[fa[id(i, j)]] = fa[id(i, j - 1)];
		int ans = 0;
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++)
			if (grid[i][j] == 1 && fa[id(i, j)] == id(i, j))ans++;
		return ans;
	}
	int minDays(vector<vector<int>>& grid) {
		if (numIslands(grid)!=1)return 0;
		for (int i = 0; i < grid.size(); i++)for (int j = 0; j < grid[0].size(); j++) {
			if (grid[i][j] == 1) {
				grid[i][j] = 0;
				if (numIslands(grid) != 1)return 1;
				grid[i][j] = 1;
			}
		}
		return 2;
	}
	int col;
};

1632. 矩阵转换后的秩

给你一个 m x n 的矩阵 matrix ，请你返回一个新的矩阵 answer ，其中 answer[row][col] 是 matrix[row][col] 的秩。

每个元素的 秩 是一个整数，表示这个元素相对于其他元素的大小关系，它按照如下规则计算：

秩是从 1 开始的一个整数。
如果两个元素 p 和 q 在 同一行 或者 同一列 ，那么：
如果 p < q ，那么 rank(p) < rank(q)
如果 p == q ，那么 rank(p) == rank(q)
如果 p > q ，那么 rank(p) > rank(q)
秩 需要越 小 越好。
题目保证按照上面规则 answer 数组是唯一的。

示例 1：


输入：matrix = [[1,2],[3,4]]
输出：[[1,2],[2,3]]
解释：
matrix[0][0] 的秩为 1 ，因为它是所在行和列的最小整数。
matrix[0][1] 的秩为 2 ，因为 matrix[0][1] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。
matrix[1][0] 的秩为 2 ，因为 matrix[1][0] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。
matrix[1][1] 的秩为 3 ，因为 matrix[1][1] > matrix[0][1]， matrix[1][1] > matrix[1][0] 且 matrix[0][1] 和 matrix[1][0] 的秩都为 2 。
示例 2：


输入：matrix = [[7,7],[7,7]]
输出：[[1,1],[1,1]]
示例 3：


输入：matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
输出：[[4,2,3],[1,3,4],[5,1,6],[1,3,4]]
示例 4：


输入：matrix = [[7,3,6],[1,4,5],[9,8,2]]
输出：[[5,1,4],[1,2,3],[6,3,1]]
 

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 500
-109 <= matrix[row][col] <= 109


class Solution {
public:
	vector<vector<int>> matrixRankTransform(vector<vector<int>>& m) {
		col = m[0].size();
		vector<int>maxR(m.size(),INT_MIN);
		vector<int>maxC(col,INT_MIN);
		vector<int>idR(m.size(),0);
		vector<int>idC(col,0);
		vector<vector<int>>g = fenzu(m);
		sort(g.begin(), g.end(), [&](const vector<int>& v1, const vector<int>& v2) {return m[v1[0] / col][v1[0] % col] < m[v2[0] / col][v2[0] % col]; });
		vector<vector<int>>ans = m;
		for (auto gi : g) {
			int tmpMax = INT_MIN;
			for (auto id : gi) {
				int r = id / col;
				int c = id % col;
				tmpMax = max(tmpMax, max(idR[r] + (m[r][c] > maxR[r]), idC[c] + (m[r][c] > maxC[c])));
			}
			for (auto id : gi) {
				int r = id / col;
				int c = id % col;
				ans[r][c] = tmpMax;
				maxR[r] = max(maxR[r], m[r][c]), maxC[c] = max(maxC[c], m[r][c]);
				idR[r] = max(idR[r], ans[r][c]), idC[c] = max(idC[c], ans[r][c]);
			}
		}
		return ans;
	}
	vector<vector<int>>fenzu(vector<vector<int>>& m)
	{
		Union opt(m.size() * col);
		map<int, int>mn;
		for (int i = 0; i < m.size(); i++) {
			mn.clear();
			for (int j = 0; j < col; j++) {
				if(mn[m[i][j]])opt.merge(i * col + j, mn[m[i][j]]-1);
				mn[m[i][j]] = i * col + j + 1;
			}
		}
		for (int j = 0; j < col; j++) {
			mn.clear();
			for (int i = 0; i < m.size(); i++) {
				if (mn[m[i][j]])opt.merge(i * col + j, mn[m[i][j]] - 1);
				mn[m[i][j]] = i * col + j + 1;
			}
		}
		return opt.getGroups();
	}
	int col;
};

2，并查集退化

一些比较简单的问题，可以用并查集做，也可以用更朴素的实现方式。

565. 数组嵌套

索引从0开始长度为N的数组A，包含0到N - 1的所有整数。找到最大的集合S并返回其大小，其中 S[i] = {A[i], A[A[i]], A[A[A[i]]], ... }且遵守以下的规则。

假设选择索引为i的元素A[i]为S的第一个元素，S的下一个元素应该是A[A[i]]，之后是A[A[A[i]]]... 以此类推，不断添加直到S出现重复的元素。

示例 1:

输入: A = [5,4,0,3,1,6,2]
输出: 4
解释: 
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.

其中一种最长的 S[K]:
S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}
 

提示：

1 <= nums.length <= 105
0 <= nums[i] < nums.length
A中不含有重复的元素。

class Solution {
public:
	int arrayNesting(vector<int>& nums) {
		map<int, int>m;
		int ans = 0;
		for (int i = 0; i < nums.size(); i++) {
			if (m[i])continue;
			m[i] = 1;
			int s = 0, k = i;
			while (++s) {
				if ((k = nums[k]) == i)break;
				m[k] = 1;
			}
			ans = max(ans, s);
		}
		return ans;
	}
};

3，并查集持久化

算法形态总结

1697. 检查边长度限制的路径是否存在（离线查询）

给你一个 n 个点组成的无向图边集 edgeList ，其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意，两个点之间可能有 超过一条边 。

给你一个查询数组queries ，其中 queries[j] = [pj, qj, limitj] ，你的任务是对于每个查询 queries[j] ，判断是否存在从 pj 到 qj 的路径，且这条路径上的每一条边都 严格小于 limitj 。

请你返回一个 布尔数组 answer ，其中 answer.length == queries.length ，当 queries[j] 的查询结果为 true 时， answer 第 j 个值为 true ，否则为 false 。

示例 1：

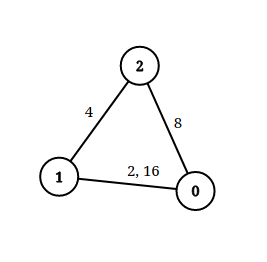
输入：n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出：[false,true]
解释：上图为给定的输入数据。注意到 0 和 1 之间有两条重边，分别为 2 和 16 。
对于第一个查询，0 和 1 之间没有小于 2 的边，所以我们返回 false 。
对于第二个查询，有一条路径（0 -> 1 -> 2）两条边都小于 5 ，所以这个查询我们返回 true 。

示例 2：

输入：n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
输出：[true,false]
解释：上图为给定数据。

提示：

  • 2 <= n <= 105
  • 1 <= edgeList.length, queries.length <= 105
  • edgeList[i].length == 3
  • queries[j].length == 3
  • 0 <= ui, vi, pj, qj <= n - 1
  • ui != vi
  • pj != qj
  • 1 <= disi, limitj <= 109
  • 两个点之间可能有 多条 边。

思路：

把边和查询都排序，用查询作为隔板把整个生成树的过程分成若干部分。

const int N = 100005; //点的最大数量

int fa[N];
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}
void merge(int i, int j)
{
	fa[find(i)] = j;
}
bool inSameSet(int i, int j)
{
	return find(i) == find(j);
}

int en; //点的数量
vector<vector<int>>p;//用数组或者vector记录点的信息，id要从0开始

struct Edge
{
	int a;//端点id
	int b;//端点id
	int dist;
};
vector<Edge> v;

bool cmp(Edge a, Edge b)
{
	return a.dist < b.dist;
}
int id(Edge a)
{
	return a.a * N + a.b;
}

vector<Edge> getEdge() // 获取所有的边
{
	// TODO 根据实际情况修改
	vector<Edge> v;
	for (int i = 0; i < p.size(); i++) {
		Edge e = { p[i][0],p[i][1],p[i][2] };
		v.push_back(e);
	}
	sort(v.begin(), v.end(), cmp);
	return v;
}
bool cmp2(vector<int>&a, vector<int>&b)
{
	return a[2] < b[2];
}

class Solution {
public:
	int vk = 0;
	bool distanceLimitedPathsExist(vector<int>& q)
	{
		while (vk<v.size() && v[vk].dist < q[2]) {
			if (!inSameSet(v[vk].a, v[vk].b))merge(v[vk].a, v[vk].b);
			vk++;
		}
		return inSameSet(q[0], q[1]);
	}
	vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
		en = n, p = edgeList;
        for (int i = 0; i < en; i++)fa[i] = i;
		v = getEdge();
        vk = 0;
		for (int i = 0; i < queries.size(); i++)queries[i].push_back(i);
		sort(queries.begin(), queries.end(), cmp2);
		vector<bool> ans(queries.size());
		for (auto& qi : queries)ans[qi[3]] = distanceLimitedPathsExist(qi);
		return ans;
	}
};

1724. 检查边长度限制的路径是否存在 II（在线查询）

一张有 n 个节点的无向图以边的列表 edgeList 的形式定义，其中 edgeList[i] = [ui, vi, disi] 表示一条连接 ui 和 vi ，距离为 disi 的边。注意，同一对节点间可能有多条边，且该图可能不是连通的。

实现 DistanceLimitedPathsExist 类：

  • DistanceLimitedPathsExist(int n, int[][] edgeList) 以给定的无向图初始化对象。
  • boolean query(int p, int q, int limit) 当存在一条从 p 到 q 的路径，且路径中每条边的距离都严格小于 limit 时，返回 true ，否则返回 false 。

示例 1:

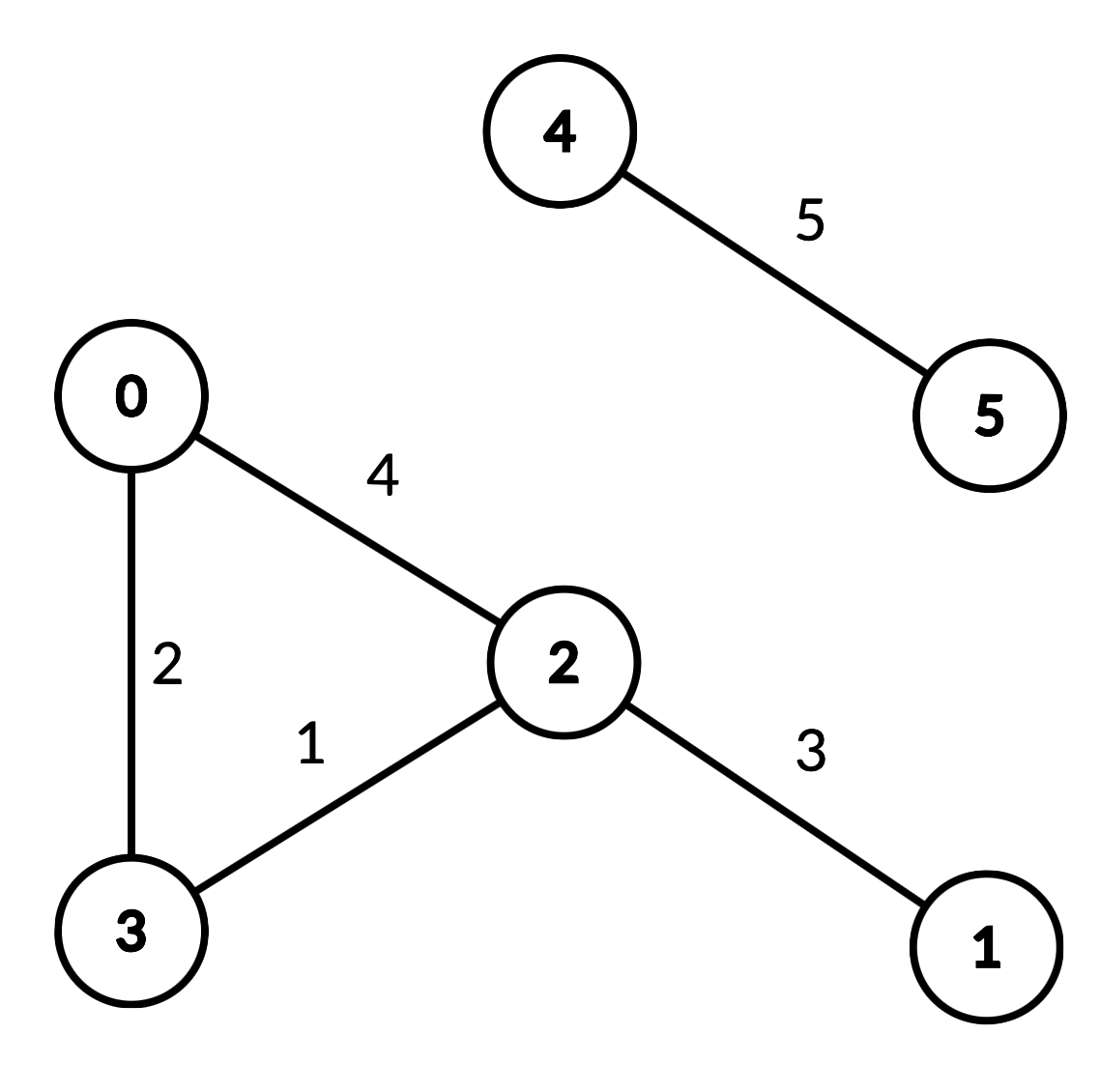
输入：
["DistanceLimitedPathsExist", "query", "query", "query", "query"]
[[6, [[0, 2, 4], [0, 3, 2], [1, 2, 3], [2, 3, 1], [4, 5, 5]]], [2, 3, 2], [1, 3, 3], [2, 0, 3], [0, 5, 6]]
输出：
[null, true, false, true, false]

解释：
DistanceLimitedPathsExist distanceLimitedPathsExist = new DistanceLimitedPathsExist(6, [[0, 2, 4], [0, 3, 2], [1, 2, 3], [2, 3, 1], [4, 5, 5]]);
distanceLimitedPathsExist.query(2, 3, 2); // 返回 true。存在一条从 2 到 3 ，距离为 1 的边，
                                          // 这条边的距离小于 2。
distanceLimitedPathsExist.query(1, 3, 3); // 返回 false。从 1 到 3 之间不存在每条边的距离都
                                          // 严格小于 3 的路径。
distanceLimitedPathsExist.query(2, 0, 3); // 返回 true。存在一条从 2 到 0 的路径，使得每条边的
                                          // 距离 < 3：从 2 到 3 到 0 行进即可。
distanceLimitedPathsExist.query(0, 5, 6); // 返回 false。从 0 到 5 之间不存在路径。

提示：

  • 2 <= n <= 104
  • 0 <= edgeList.length <= 104
  • edgeList[i].length == 3
  • 0 <= ui, vi, p, q <= n-1
  • ui != vi
  • p != q
  • 1 <= disi, limit <= 109
  • 最多调用 104 次 query 。

 思路：

离线查询可以对查询请求进行排序，但是在线不行，在线更难，所以本题支持的查询次数是10^4，而离线查询支持的是10^5次查询。

考虑去重，实际上不同的查询次数不会超过边数，所以考虑做成离线处理+大量存储+在线查询。

const int N = 10005; //点的最大数量
int fas[10000][N];
int* fa;
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}
void merge(int i, int j)
{
	fa[find(i)] = j;
}
bool inSameSet(int i, int j)
{
	return find(i) == find(j);
}

int en; //点的数量
vector<vector<int>>p;//用数组或者vector记录点的信息，id要从0开始

struct Edge
{
	int a;//端点id
	int b;//端点id
	int dist;
};
vector<Edge> v;

bool cmp(Edge a, Edge b)
{
	return a.dist < b.dist;
}

vector<Edge> getEdge() // 获取所有的边
{
	// TODO 根据实际情况修改
	vector<Edge> v;
	for (int i = 0; i < p.size(); i++) {
		Edge e = { p[i][0],p[i][1],p[i][2] };
		v.push_back(e);
	}
	sort(v.begin(), v.end(), cmp);
	return v;
}

class DistanceLimitedPathsExist {
public:
	int vk = 0, fk = 0;
	bool distanceLimitedPathsExist(Edge& q)
	{
		while (vk < v.size() && v[vk].dist <= q.dist) {
			if (!inSameSet(v[vk].a, v[vk].b))merge(v[vk].a, v[vk].b);
			vk++;
		}
		return inSameSet(q.a,q.b);
	}
	DistanceLimitedPathsExist(int n, vector<vector<int>>& edgeList) {
		en = n, p = edgeList;
		fa = new int[n];
		for (int i = 0; i < n; i++)fa[i] = i;
		v = getEdge();
		for (auto& vi : v) {
			vl.push_back(vi.dist);
			distanceLimitedPathsExist(vi);
			for(int i=0;i<n;i++)fas[fk][i] = fa[i];
			fk++;
		}
	}

	bool query(int p, int q, int limit) {
		int k = lower_bound(vl.begin(), vl.end(), limit)- vl.begin();
		if (k == 0)return false;
		fa = fas[k-1];
		return inSameSet(p, q);
	}
	vector<int>vl;
};

时间1040 ms  内存520.2 MB

做个简单的简化

const int N = 10005; //点的最大数量
int fas[10000][N];
int* fa;
inline int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}
void merge(int i, int j)
{
	fa[find(i)] = j;
}
bool inSameSet(int i, int j)
{
	return find(i) == find(j);
}

int en; //点的数量
vector<vector<int>>p;//用数组或者vector记录点的信息，id要从0开始

struct Edge
{
	int a;//端点id
	int b;//端点id
	int dist;
};
vector<Edge> v;

bool cmp(Edge a, Edge b)
{
	return a.dist < b.dist;
}

vector<Edge> getEdge() // 获取所有的边
{
	// TODO 根据实际情况修改
	vector<Edge> v;
	for (int i = 0; i < p.size(); i++) {
		Edge e = { p[i][0],p[i][1],p[i][2] };
		v.push_back(e);
	}
	sort(v.begin(), v.end(), cmp);
	return v;
}

class DistanceLimitedPathsExist {
public:
	int fk = 0;
	DistanceLimitedPathsExist(int n, vector<vector<int>>& edgeList) {
		en = n, p = edgeList;
		fa = new int[n];
		for (int i = 0; i < n; i++)fa[i] = i;
		v = getEdge();
		for (auto& vi : v) {
			vl.push_back(vi.dist);
			if (!inSameSet(vi.a, vi.b))merge(vi.a, vi.b);
			for(int i=0;i<n;i++)fas[fk][i] = fa[i];
			fk++;
		}
	}

	bool query(int p, int q, int limit) {
		int k = lower_bound(vl.begin(), vl.end(), limit)- vl.begin();
		if (k == 0)return false;
		fa = fas[k-1];
		return inSameSet(p, q);
	}
	vector<int>vl;
};

时间964 ms 内存520.2 MB

再改成离散化的写法，不存全部的fa数组，而且间隔存：

const int N = 10005; //点的最大数量
int fas[1000][N];
int* fa;
int find(int x)	//找祖先
{
	if (fa[x] == x)return x;
	return fa[x] = find(fa[x]);
}
void merge(int i, int j)
{
	fa[find(i)] = j;
}
bool inSameSet(int i, int j)
{
	return find(i) == find(j);
}

int en; //点的数量
vector<vector<int>>p;//用数组或者vector记录点的信息，id要从0开始

struct Edge
{
	int a;//端点id
	int b;//端点id
	int dist;
};
vector<Edge> v;

bool cmp(Edge a, Edge b)
{
	return a.dist < b.dist;
}

vector<Edge> getEdge() // 获取所有的边
{
	// TODO 根据实际情况修改
	vector<Edge> v;
	for (int i = 0; i < p.size(); i++) {
		Edge e = { p[i][0],p[i][1],p[i][2] };
		v.push_back(e);
	}
	sort(v.begin(), v.end(), cmp);
	return v;
}

class DistanceLimitedPathsExist {
public:
	int fk = 0;
	int ratio = 10;
	vector<int>vl;
	DistanceLimitedPathsExist(int n, vector<vector<int>>& edgeList) {
		en = n, p = edgeList;
		fa = new int[n];
		for (int i = 0; i < n; i++)fa[i] = i;
		v = getEdge();
		for (auto& vi : v) {
			vl.push_back(vi.dist);
			if (!inSameSet(vi.a, vi.b))merge(vi.a, vi.b);
			if(fk% ratio ==0)for(int i=0;i<n;i++)fas[fk/ratio][i] = fa[i];
			fk++;
		}
	}

	bool query(int p, int q, int limit) {
		int k = lower_bound(vl.begin(), vl.end(), limit)- vl.begin()-1;
		if (k < 0)return false;
		for (int i = 0; i < en; i++){
			fa[i] = fas[k/ ratio][i];
		}
		for(int i=k/ratio*ratio;i<=k;i++){
			if (!inSameSet(v[i].a, v[i].b))merge(v[i].a, v[i].b);
		}
		return inSameSet(p, q);
	}
};

时间1556 ms 内存178.4 MB

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/184900.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

浅谈对 Binder 的理解

浅谈对 Binder 的理解

文章目录Binder 是干嘛的&#xff1f;Binder 的意义binder 的通信架构如何启动 binder 机制binder 通信binder 驱动的分层架构图需要了解的知识 binder 是干嘛的binder 的存在意义是怎样的Android 为什么选择 binder 作为主要的 ipc 通信机制&#xff1f;binder 的架构 Binde…
阅读更多...
Vue 3 介绍

Vue 3 介绍

Vue 3 介绍Vue3 动机 和 新特性Vite 的使用为什么选 Vite为什么要学习 vue 3Vue是国内最火的前端框架Vue 3 于 2022 年 2 月 7 日星期一成为新的默认版本&#xff01;Vue3性能更高&#xff0c;体积更小Vue3.0在经过一年的迭代后&#xff0c;越来越好用 目前已支持 vue3 的UI组…
阅读更多...
Python简介安装与PyCharm安装使用

Python简介安装与PyCharm安装使用

一、Python简介 Python官方文档&#xff1a;https://docs.python.org/zh-cn/3/ Python 3.x 已经将 UTF-8 作为默认的源文件编码格式。 1、Python简介 Python 是一门开源免费、通用型的脚本编程语言&#xff0c;它上手简单&#xff0c;功能强大&#xff0c;坚持「极简主义」&am…
阅读更多...
Visual Studio Code (VS Code) - 列块编辑与查找

Visual Studio Code (VS Code) - 列块编辑与查找

Visual Studio Code (VS Code) - 列块编辑与查找1. 列块选择 Shift Alt 鼠标左键&#xff0c;进行列编辑&#xff0c;批量增删改。 在选定位置按下滚轮键 (鼠标中键) 不放&#xff0c;移动鼠标完成多列选择。 2. 页面双列布局 查看 -> 编辑器布局 -> 双列 3. 查…
阅读更多...
linux使用ZLMediaKit搭建rtsp服务器

linux使用ZLMediaKit搭建rtsp服务器

入门小菜鸟&#xff0c;希望像做笔记记录自己学的东西&#xff0c;也希望能帮助到同样入门的人&#xff0c;更希望大佬们帮忙纠错啦~侵权立删。 致敬rtsp 服务器搭建_音视频开发老马的博客-CSDN博客_rtsp服务器 这里是参考上面链接的介绍再进行一些自己遇到的问题的补充。 一…
阅读更多...
一种化学荧光探针945928-17-6，TAMRA alkyne,5-isomer，四甲基罗丹明-炔基

一种化学荧光探针945928-17-6，TAMRA alkyne,5-isomer，四甲基罗丹明-炔基

【中文名称】5-四甲基罗丹明-炔基【英文名称】 TAMRA alkyne,5-isomer【CAS】945928-17-6【分子式】C28H25N3O4【分子量】467.53【纯度标准】95%【包装规格】5mg&#xff0c;10mg&#xff0c;25mg【是否接受定制】可进行定制&#xff0c;定制时间周期上面可以和我们进行沟通【外…
阅读更多...
redis常用数据类型和应用场景

redis常用数据类型和应用场景

我们都知道 Redis 提供了丰富的数据类型&#xff0c;常见的有五种&#xff1a;String&#xff08;字符串&#xff09;&#xff0c;Hash&#xff08;哈希&#xff09;&#xff0c;List&#xff08;列表&#xff09;&#xff0c;Set&#xff08;集合&#xff09;、Zset&#xff0…
阅读更多...
稀疏表（ST表，Sparse Table）

稀疏表（ST表，Sparse Table）

ST表用来解决区间最值问题&#xff08;也可以解决区间gcd&#xff09; 利用倍增的思想&#xff0c;O(nlog⁡2n)O\left(n\log_2 n\right)O(nlog2​n)预处理&#xff0c;O(1)O\left(1\right)O(1)区间查询 令f(i,j)f\left(i,j\right)f(i,j)表示区间[i,i2j−1]\left[i,i2^j-1\right…
阅读更多...
TypeScript 学习笔记总结(二)

TypeScript 学习笔记总结(二)

TypeScript 笔记记录&#xff0c;侧重于接口&#xff0c;对象等内容。 文章目录一、 TS 面向对象二、TS 类三、TS 继承四、TS super关键字五、TS 抽象类六、TS 接口七、TS 属性封装八、TS 泛型一、 TS 面向对象 js也是面向对象的&#xff0c;并不是面向过程的。 下面&#xf…
阅读更多...
虹科案例 | AR数字化解决方案在石油与天然气领域“大放异彩”

虹科案例 | AR数字化解决方案在石油与天然气领域“大放异彩”

石油和天然气在当今人类社会中扮演着重要角色&#xff0c;但是石油和天然气的开采&#xff0c;却是耗费成本巨大的工程&#xff0c;石油和天然气公司也在不断寻找着能帮助他们降低运营成本并提高效率的好方法。 事实上&#xff0c;AR技术解决方案能帮助这些公司实现他们的目标…
阅读更多...
Linux[安装gitlab笔记]

Linux[安装gitlab笔记]

参考文章&#xff1a;https://www.jianshu.com/p/2cb10c11813d CentOS7下安装gitlab中文版 前提&#xff1a; 下载文件&#xff1a;gitlab-ce-12.9.2-ce.0.el7.x86_64.rpm 地址1&#xff1a;https://packages.gitlab.com/gitlab/gitlab-ce 地址2&#xff1a;https://mirrors.…
阅读更多...
JVM——类加载与字节码技术（3）

JVM——类加载与字节码技术（3）

目录四、类加载阶段4.1 加载4.2 链接4.3 初始化五、类加载——练习练习1练习2四、类加载阶段 4.1 加载 ① 将类的字节码载入方法区&#xff08;1.8后为元空间&#xff0c;在本地内存中&#xff09;中&#xff0c;内部采用 C 的 instanceKlass ● _java_mirror 即 java 的类镜…
阅读更多...
大数据技术架构(组件)10——Hive：集合函数类型转化函数

大数据技术架构(组件)10——Hive：集合函数类型转化函数

1.4.3、集合函数1.4.3.1、size select map(a,1,b,2),size(map(a,1,b,2)),array(1,2,3,4),size(array(1,2,3,4));1.4.3.2、map_keysselect map(a,1,b,2), map_keys(map(a,1,b,2));1.4.3.3、map_valuesselect map(a,1,b,2), map_values(map(a,1,b,2));1.4.3.4、array_containssel…
阅读更多...
中国国际电子商务中心与易观分析联合发布：2022年3季度全国网络零售发展指数同比增长1.5%

中国国际电子商务中心与易观分析联合发布：2022年3季度全国网络零售发展指数同比增长1.5%

近日&#xff0c;中国国际电子商务中心与易观分析联合发布2022年3季度“全国网络零售发展指数”及其分指数。2022年3季度全国网络零售发展指数同比增长1.5%&#xff0c;环比下降2.9%。随着稳经济一揽子政策和接续措施全面落地显效&#xff0c;生产加快回暖&#xff0c;经济平稳…
阅读更多...
vmstat、free、df、iostat、sar

vmstat、free、df、iostat、sar

1. vmstat看CPU vmstat -n 2 3 一般vmstat工具的使用是通过两个数字参数来完成的&#xff0c;第一个参数是采样的时间间隔数单位是秒&#xff0c;第二个参数是采样的次数 -procs r:运行和等待CPU时间片的进程数&#xff0c;原则上1核的CPU的运行队列不要超过2&#xff0c;整个…
阅读更多...
Softing为Endress+Hauser提供过程自动化连接解决方案

Softing为Endress+Hauser提供过程自动化连接解决方案

一 背景 恩德斯豪斯&#xff08;EndressHauser&#xff09;是一家总部位于瑞士的过程工业自动化解决方案的全球领军企业&#xff0c;致力于为过程工业及实验室自动化领域提供测量仪器、服务和解决方案。其产品被广泛应用于石油、化工、制药、食品饮料以及废水处理等过程自动化…
阅读更多...
银河麒麟V10操控系统Qt安装

银河麒麟V10操控系统Qt安装

下载安装镜像申请试用https://www.kylinos.cn/support/trial.html&#xff0c;根据CPU架构选择要下载的安装包。AMD、Intel的CPU下载银河麒麟桌面操作系统V10 AMD64版本&#xff0c;我下载的Kylin-Desktop-V10-SP1-HWE-Release-2203-X86_64.iso制作系统安装启动U盘下载制作启动…
阅读更多...
1. kafka-提高生产者吞吐量

1. kafka-提高生产者吞吐量

kafka的基础使用知识不在这篇文章阐述&#xff0c;默认读者都会使用 首先kafka的生产者原理&#xff0c;如下。图来自网上 上面的图可能不全&#xff0c; 我再详细描述下&#xff0c;在消息发送过程中&#xff0c;设计到两个线程main和sender线程&#xff1b; &#xff08;1…
阅读更多...
Java接口——子接口是否能直接通过子接口名调用父接口类方法

Java接口——子接口是否能直接通过子接口名调用父接口类方法

Java9允许在接口中定义默认方法和类方法&#xff0c;为接口增加了一种私有方法&#xff0c;也可以提供实现。 接口就是定义一组通用的方法&#xff0c;就像U盘&#xff0c;只要是USB接口大部分都可以在电脑上使用&#xff0c;电脑无需关心U盘内部怎么实现&#xff0c;只需要告…
阅读更多...
浅谈python中@装饰器 - 附例子（含类装饰器与函数装饰器）

浅谈python中@装饰器 - 附例子（含类装饰器与函数装饰器）

浅谈python中装饰器 文章目录浅谈python中装饰器关于装饰器&#xff08;decorator&#xff09;小总结关于&#xff08;语法糖&#xff09;进阶装饰器顺序装饰器 & 参数End提到的使用首先要先讲一下装饰器的概念 关于装饰器&#xff08;decorator&#xff09; 先来看看官方…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023