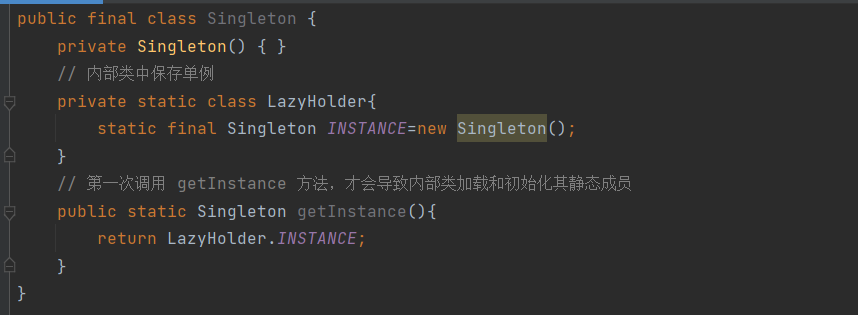
ST表用来解决区间最值问题（也可以解决区间gcd）
利用倍增的思想，$O\left(n{\log }_{2}n\right)$预处理，$O\left(1\right)$区间查询

令$f\left(i,j\right)$表示区间$\left[i,i+2^j-1\right]$
$f\left(i,0\right)=a_i$
$f\left(i,j\right)=\max \left(f\left(i,j-1\right),f\left(i+2^{j-1},j-1\right)\right)$
对于查询$\left[l,r\right]$,令$s=\lfloor {\log }_2\left(r-l+1\right)\rfloor$
通过$\max \left(f\left[l,l+2^s-1\right],f\left[r-2^s+1,r\right]\right)$来找到$\left[l,r\right]$的最大值
（为什么不是$\left[l+2^s,r\right]$?因为有可能越界）

剩下的就是可以考虑预处理${\log }_2$

int logn[N] = { -1, 0 };//floor( log2 n )
//预处理log2
for (int i = 2; i <= n; ++i) {
	logn[i] = logn[i >> 1] + 1;
}

// pre C++20
int log2_floor(unsigned long long i) {
    return i ? __builtin_clzll(1) - __builtin_clzll(i) : -1;
}

// C++20
#include <bit>
int log2_floor(unsigned long i) {
    return std::bit_width(i) - 1;
}

洛谷P3865

#include<cstdio>
#include<algorithm>

const int N = 1e5 + 5;

int logn[N] = { -1, 0 };//floor( log2 n )
int st[N][21];

int main() {
	int n, m;
	scanf("%d%d", &n, &m);

	//预处理log2
	for (int i = 2; i <= n; ++i) {
		logn[i] = logn[i >> 1] + 1;
	}
	
	for (int i = 1; i <= n; ++i) {
		scanf("%d", &st[i][0]);
	}

	//预处理
	for (int j = 1; j <= logn[n]; ++j) {
		for (int i = 1; i + (1 << j) - 1 <= n; ++i) {
			st[i][j] = std::max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);

		}
	}

	while (m--) {
		int l, r;
		scanf("%d%d", &l, &r);
		int s = logn[r - l + 1];
		printf("%d\n", std::max(st[l][s], st[r - (1 << s) + 1][s]));
	}

	return 0;
}