文章目录
- 可持久化线段树(主席树)
- 建树前准备!
- 初始化建树!
- 更新操作!
- 区间查询!
- AC code
可持久化线段树(主席树)
可持久化线段树指的是可持久化权值线段树,关于权值线段树可以看我这篇博客:
权值线段树详解+模板
下面我直接用主席树这个名称来介绍写可持久化权值线段树
引入:
对于一颗权值线段树,我们要往里面添加n个数字,我们知道,这很容易实现,只需要一个for循环,然后调用n次update函数即可(update函数具有添加元素的功能,详见《权值线段树博文》)。
但是如果需要一个记忆化的过程,即我们每添加一个元素都需要记住这个权值线段树的状态,以便于我们对历史的操作,那么如果只使用权值线段树,则我们需要n个权值线段树同时保存状态,对于非常多的元素,我们就需要保存非常多的权值线段树,这样做空间一定会爆炸,有没有什么办法可以使我们有效的保存历史的状态呢?? 主席树提供了这一功能
先来看看每次修改或者插入一个元素往权值线段树,这个权值线段树的每个时刻的状态吧:
- 我们以插入元素 [1,2,3,4,3] 为例吧
这是元素逐一插入的过程:
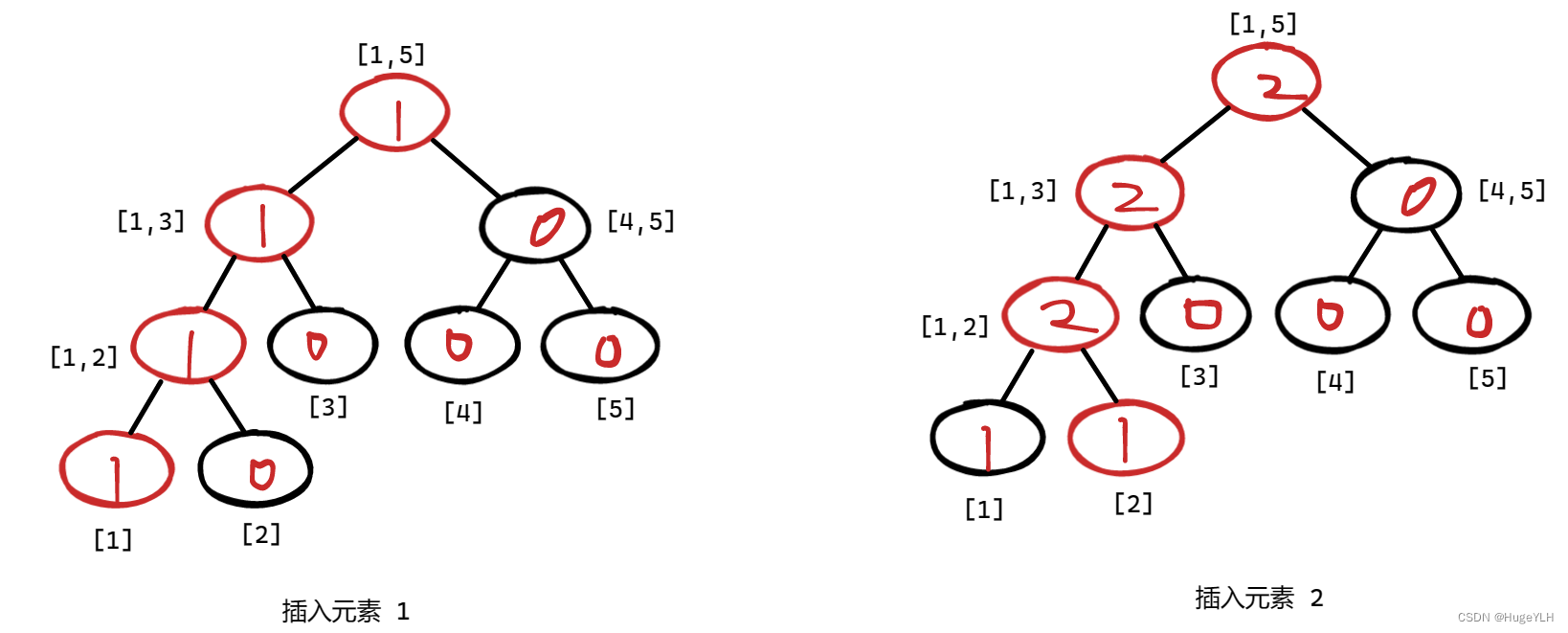
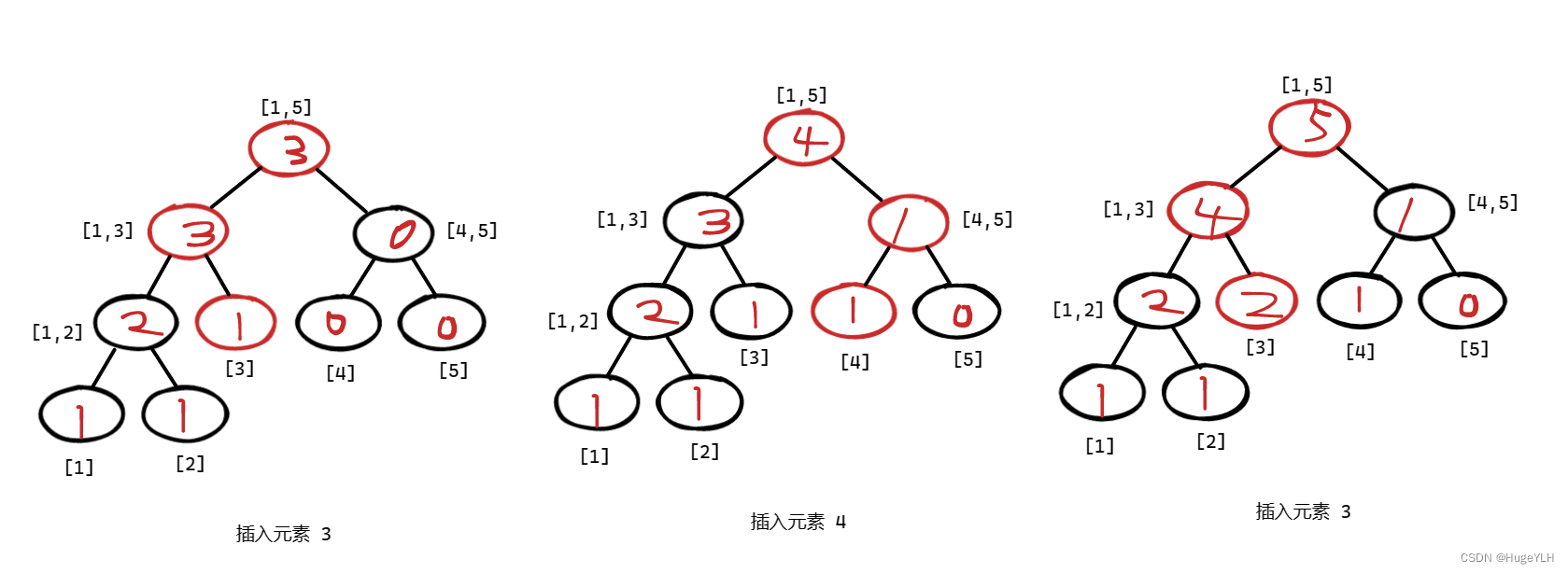
这样我们就完成了五个权值线段树的构建构成,但是我们发现,貌似每次的插入一个元素,修改的线段树的结构只与这个插入的元素有关
- 每次修改只会是添加的值到根节点的一条链上的值发生了变化(如红色链所示),而其它的节点和上次修改结束后的都是一样的。
- 我们貌似不用每次都新建一个权值线段树,直接新建一条表示值发生变化的链不就好了
只添加链,不适用新建权值线段树的方式创建的主席树:
- 这种只添加链的方式构建的线段树就是主席树
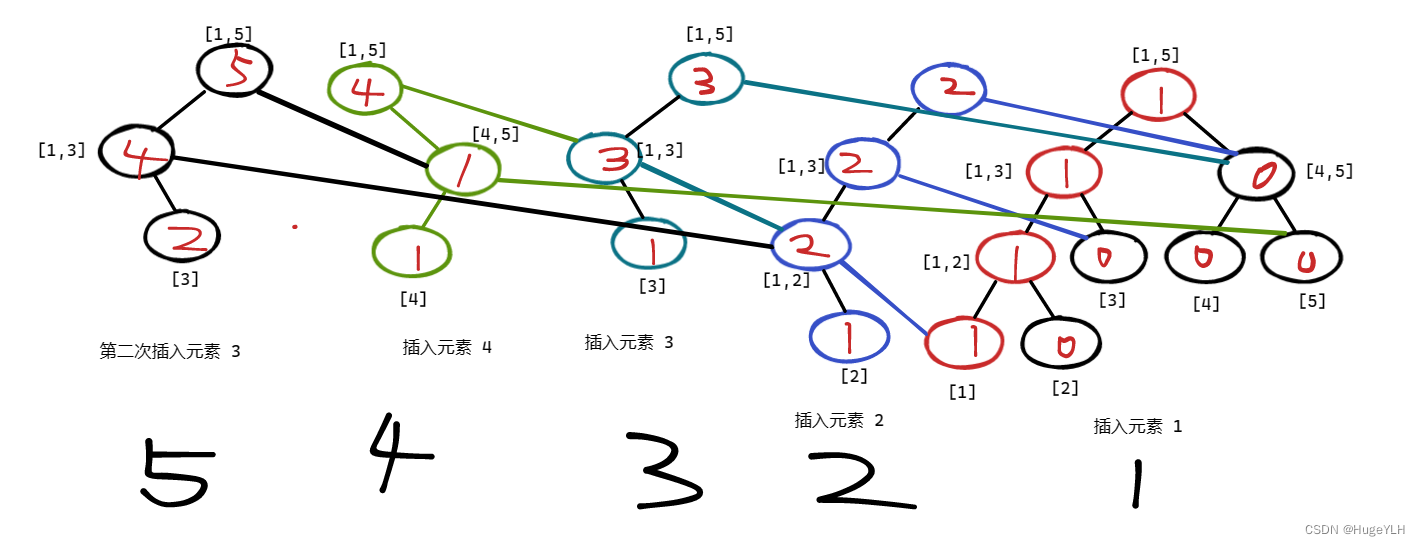
恶心!!!!!!!!!!!!!!!!!!!!!!!!!
不要惊慌!!!!!!! 这就是只添加链的主席树。
其实还是很清晰的,每次找到要修改的值所会影响的节点链,然后单独添加一颗链就好了。
观察这颗主席树,我们可以发现几个性质:
- 新添加的节点链条上:叶子节点不会连接原有节点,非叶子节点一定是一端连接新的链条节点,另一端连接原有节点。
- 每次添加的节点链条的长度(深度)是logN
- 主席树有很多根,图中有5个,每一个根都可以单独形成一个新的权值线段树
因此,主席树就是一个可以保存历史的权值线段树,如何访问历史呢? 我们前面提到过,每一个根可以组成一个单独的线段树,而每一个根节点都可以用一个唯一的编号表示。用一个root数组存储所有历史中的根节点。
主席树只会对部分节点进行复制,并且每一次复制的节点个数是log(n)。我们每一次想询问一个版本的线段树,就可以在那个版本的根构成的线段树(使用root获取版本)中询问。
主席树对于处理任意区间第k大/小这种问题具有非常明显的优势,前面我们说过权值线段树也可以处理区间第k大,但是权值线段树必须是整个区间的第k大,对于任意区间无法得出答案
我们以例题为例,说明主席树的代码实现:区间第k小的元素
来看看代码实现:
建树前准备!
注意:
- btree表示我们的主席树的每一个节点,其中 l 和 r 表示左右孩子节点的编号,而不是 l2 和 l2+1,val表示数字出现的次数 (请注意,这个地方非常重要)
- 对于N个历史,假设N为 1e6 ,则最多会存在 N+ NlogN 个节点,则我们最好这个主席树弄成 N的32倍以上。
- root存储每一个根节点编号,top表示顶层编号
int n, m;
const int N = 1e6 + 10;
int nums[N<<2], top, root[N<<2];
struct node
{
int l, r, val;
friend ostream& operator<<(ostream& os, node& p)
{
//dbg
os << p.l << " " << p.r << " " << p.val << endl;
return os;
}
}btree[N*40]; //N+N(log2(N))=3kw ...
初始化建树!
注意我们的每个节点的区间 l,r需要进行赋值!!!,通过递归与回溯可以完成这一过程,其他过程与普通线段树一致
另外node表示当前节点的编号,随着递归与回溯起到给节点的 l,r赋值的作用。还可以是这样的写法:把node参数设置为引用,则build就是void了,直接在参数内修改,我比较喜欢按返回值的形式来写。
划重点!!!!!!!!!!!!!!!!!!!!
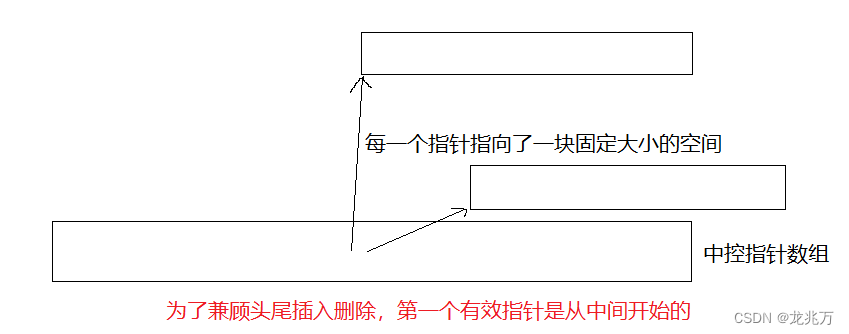
关于主席树的节点 l 和 r的值,有必要再说明以下:(假设的图,与题无关)
- 红色: val值
- 绿色:节点的 l 和 r值
- 黑色数字: 节点编号
- 关于根节点的 l 和 r 分别是2编号和7编号,其中2为左孩子的编号,7为右孩子的编号
- 对于左孩子2也同理,3和6分别表示其左右孩子的编号
- 叶子节点没有 l 和 r 编号
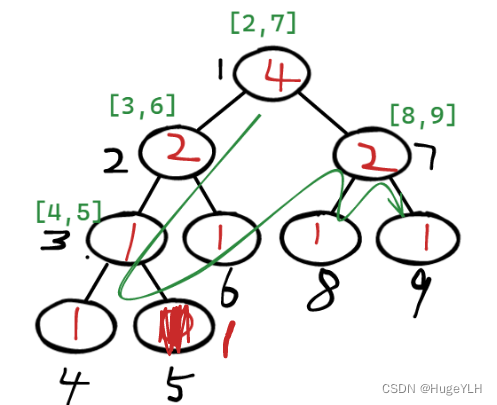
这是怎么形成的呢???就是通过 node 的递归与回溯实现的
//初始化建树
int build(int node,int pl,int pr)
{
node=++top;
tree[node].val=0;
if (pl==pr)
{
return node; //返回当前节点编号,传递给父节点
}
int mid=(pl+pr)>>1;
tree[node].l=build(node,pl,mid); //递归左子树,完成当前节点l的赋值
tree[node].r=build(node,mid+1,pr); //递归右子树,完成当前节点r的赋值
return node; //返回当前当前编号,传递给父节点
}
更新操作!
- 注意到clone函数,我们必须新建一条节点链,而不是整个权值线段树,因此我们必须复制每一个原有的节点,还需要注意复制的过程是递归中进行的
- 另外关于clone,你是否觉得它放在第一行会不会造成整颗线段树全都复制了??? 这其实是不可能造成的,请看下面的递归部分,当修改的loc位置在某一个区间中,则会递归到这个节点,只要是递归到了这个区间,则这个区间一定是会被修改的,所以说也一定是需要新建节点的(请认真理解这句话),所以clone函数完成了对每一个需要修改的节点形成了一条新的节点链条,而不是整棵树。
inline int clone(int pre)
{
/*从原始节点复制一个节点数据*/
//pre为原有节点的编号
++top;
tree[top].l=tree[pre].l;
tree[top].r=tree[pre].r;
tree[top].val=tree[pre].val+1; //这个元素出现的次数+1
return top; //返回新建的节点的编号
}
- loc:表示修改的节点位置
- clone后新建了一个节点,则返回这个新的节点编号,此时要完成对这个新的节点 l,r的更新操作,即有的l不需要更新(未修改的),有的r需要更新为新的区间(修改的)
//更新
int update(int pre,int pl,int pr,int loc)
{
int cur=clone(pre); //新建一个节点,同时返回这个新的节点编号
if (pl==pr)
{
return cur; //返回当前节点编号
}
int mid=(pl+pr)>>1;
if (loc<=mid)
{
//完成当前节点的l的update
tree[cur].l=update(tree[cur].l,pl,mid,loc);
}
else
{
//完成当前节点r的update
tree[cur].r=update(tree[cur].r,mid+1,pr,loc);
}
return cur; //返回当前节点编号,实现对子根节点的lr赋值
}
更新操作示意图:
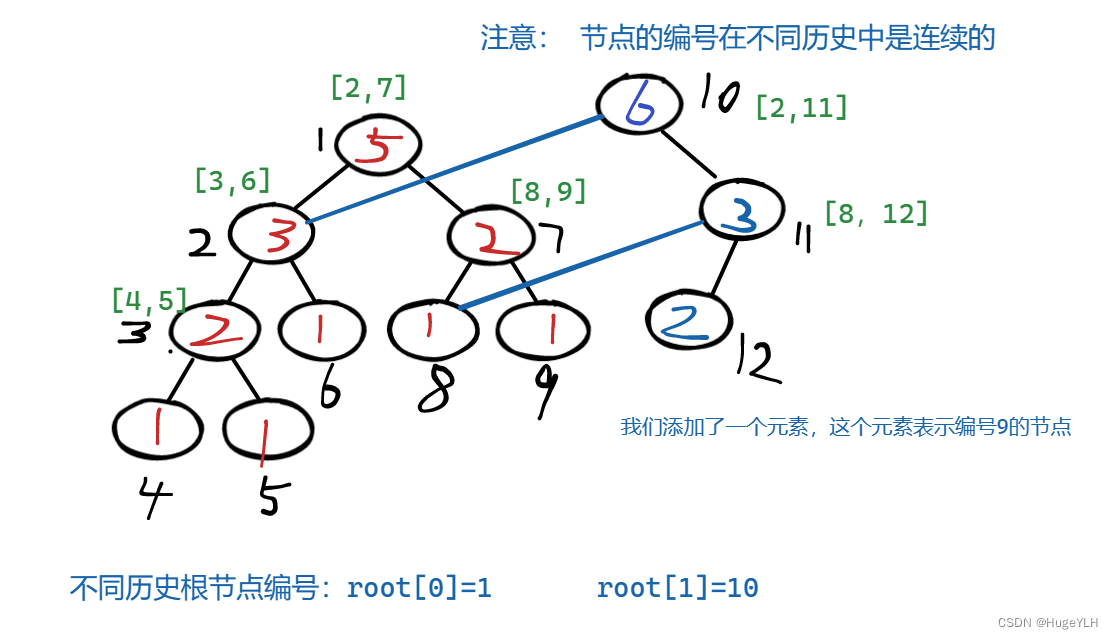
区间查询!
发明者的原话:“对于原序列的每一个前缀[1···i]建立出一棵线段树维护值域上每个数出现的次数,则其树是可减的”
可以加减的理由:主席树的每个节点保存的是一颗线段树,维护的区间信息,结构相同,因此具有可加减性
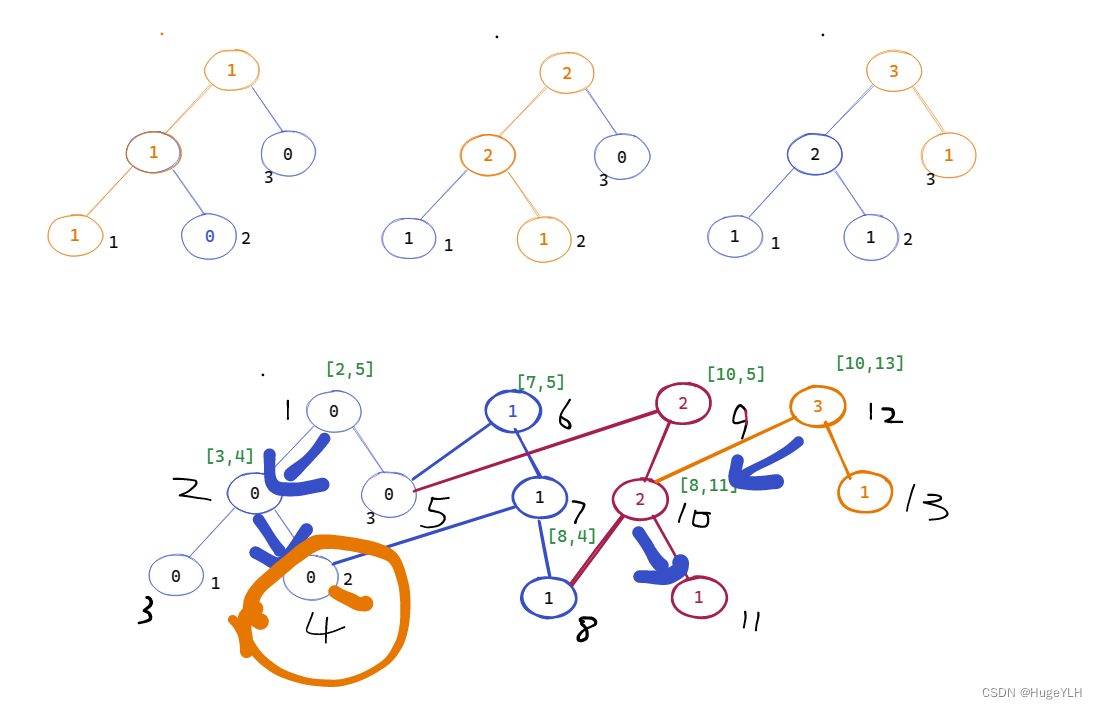
详细查询过程: 原始区间: [1,2,3] 查询 1到3 里的第二小的值(应该为2)
- 我们查询 l=1 r=3 k=2 因此这样查询:query(sum[r]) - query(sum[l-1])
- 首先进入query函数,当前为12编号根节点,前一个为1编号根节点。对于编号12的根节点的左孩子编号为10,编号为1的根节点左孩子是2,让sum[10]-sum[2],sum记录的是此节点的val,相减得2,因为k=2,所以进入左子树递归。
- 当前为10编号根节点,前一个为2编号根节点。对于编号10的根节点的左孩子编号为8,编号为2的根节点左孩子是3,让d=(sum[8]-sum[3]),sum记录的是此节点的val,相减得1,因为k=2,所以进入右子树递递归,同时 k - d
- 当前为11编号根节点,前一个为4编号根节点。此时已经到达了叶子节点,返回 pl或者pr,得结果为 2(此时pl== pr==2,达到编号为4的叶子节点)
//查询
int query(int pre,int cur,int pl,int pr,int k)
{
int ans=0;
//sum[lc[cur]]-sum[lc[pre]]
int L1=tree[cur].l; //当前节点的l位置
int L2=tree[pre].l; //当前节点的pre时刻的l位置
//通过两个时刻同一位置的val的相减,得到这个节点所包含的元素个数
//即表示了在[pl,pr]查询区间内,有多少个元素位于这个节点的子区间内
int num=tree[L1].val-tree[L2].val;
if (pl==pr)
{
return pl; //到达叶子节点,叶子节点是我们查询的节点,直接返回pl或者pr都行
}
int mid=(pl+pr)>>1;
if (num>=k)
{
//递归查询左子树
return query(tree[pre].l,tree[cur].l,pl,mid,k);
}
else
{
//递归查询右子树
return query(tree[pre].r,tree[cur].r,mid+1,pr,k-num);
}
}
AC code
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using DB = double;
using PI = pair<int, int>;
using PL = pair<LL, LL>;
template<typename T> using v = vector<T>;
constexpr auto INF = 0X3F3F3F3F;
template<typename T1, typename T2> using umap = unordered_map<T1, T2>;
#define ic std::ios::sync_with_stdio(false);std::cin.tie(nullptr)
template <typename ConTainermap> void dbgumap(ConTainermap c); //output umap
template <typename _Ty> void dbg(_Ty nums[], int n);
#if 1
#define int LL
#endif
inline int read(); //fast input
inline void write(int x); //fast output
//TODO: Write code here
int n, m;
const int N = 2e5 + 10;
int nums[N << 2], top, temp[N << 2], root[N << 2];
struct node
{
int l, r, val;
}tree[N << 5];
inline int clone(int pre)
{
/*从原始节点复制一个节点数据*/
//pre为原有节点的编号
++top;
tree[top].l = tree[pre].l;
tree[top].r = tree[pre].r;
tree[top].val = tree[pre].val + 1;
return top; //返回新建的节点的编号
}
//初始化建树
int build(int node, int pl, int pr)
{
node = ++top;
tree[node].val = 0;
if (pl == pr)
{
return node; //返回当前节点编号,传递给父节点
}
int mid = (pl + pr) >> 1;
tree[node].l = build(node, pl, mid); //递归左子树,完成当前节点l的赋值
tree[node].r = build(node, mid + 1, pr); //递归右子树,完成当前节点r的赋值
return node; //返回当前当前编号,传递给父节点
}
//更新
int update(int pre, int pl, int pr, int loc)
{
int cur = clone(pre); //新建一个节点,同时返回这个新的节点编号
if (pl == pr)
{
return cur; //返回当前节点编号
}
int mid = (pl + pr) >> 1;
if (loc <= mid)
{
//完成当前节点的l的update
tree[cur].l = update(tree[cur].l, pl, mid, loc);
}
else
{
//完成当前节点r的update
tree[cur].r = update(tree[cur].r, mid + 1, pr, loc);
}
return cur; //返回当前节点编号,实现对子根节点的lr赋值
}
//查询
int query(int pre, int cur, int pl, int pr, int k)
{
int ans = 0;
//sum[lc[cur]]-sum[lc[pre]]
int L1 = tree[cur].l; //当前节点的l位置
int L2 = tree[pre].l; //当前节点的pre时刻的l位置
//通过两个时刻同一位置的val的相减,得到这个节点所包含的元素个数
//即表示了在[pl,pr]查询区间内,有多少个元素位于这个节点的子区间内
int num = tree[L1].val - tree[L2].val;
if (pl == pr)
{
return pl; //到达叶子节点,叶子节点是我们查询的节点,直接返回pl或者pr都行
}
int mid = (pl + pr) >> 1;
if (num >= k)
{
//递归查询左子树
return query(tree[pre].l, tree[cur].l, pl, mid, k);
}
else
{
//递归查询右子树
return query(tree[pre].r, tree[cur].r, mid + 1, pr, k - num);
}
}
signed main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
scanf("%lld", &nums[i]);
temp[i] = nums[i];
}
sort(temp + 1, temp + 1 + n);
int len = unique(temp + 1, temp + 1 + n) - temp - 1;
root[0] = build(0, 1, len); //构建空树,root[0]记录
// 1 2 3 4 5
// l r [3,5] 2
for (int i = 1; i <= n; i++)
{
/// @brief 离散化的时候!!!!!!!!!!!!!!!
/// @return lower_bound查找的是nuums[i]在temp中的位置,而temp的取值范围为[1,len+1],其中len为去重后的长度,不是原始的长度n!!!!!!!!!!!!!!!!!!
int loc = lower_bound(temp + 1, temp + 1 + len, nums[i]) - temp;
//root[i]记录每次更新后的新的树,其中每一棵树都是一个《权值线段树》
root[i] = update(root[i - 1], 1, len, loc);
}
int ans = 0;
while (m--)
{
int l, r, k;
scanf("%lld%lld%lld", &l, &r, &k);
//查询[l,r]区间,即完成root[r]-root[l-1]的计算
ans = query(root[l - 1], root[r], 1, len, k);
printf("%lld\n", temp[ans]);
}
return 0;
}
template <typename _Ty>
void dbg(_Ty nums[], int n)
{
for (int i = 1; i <= n; i++)
{
cout << nums[i] << " ";
}
cout << endl;
}
template <typename ConTainermap>
void dbgumap(ConTainermap c)
{
for (auto& x : c)
{
cout << "key:" << x.first << " val:" << x.second << endl;
}
}
inline int read()
{
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9')
{
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
{
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
inline void output(int x)
{
static int sta[35];
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
while (top) putchar(sta[--top] + 48);
}