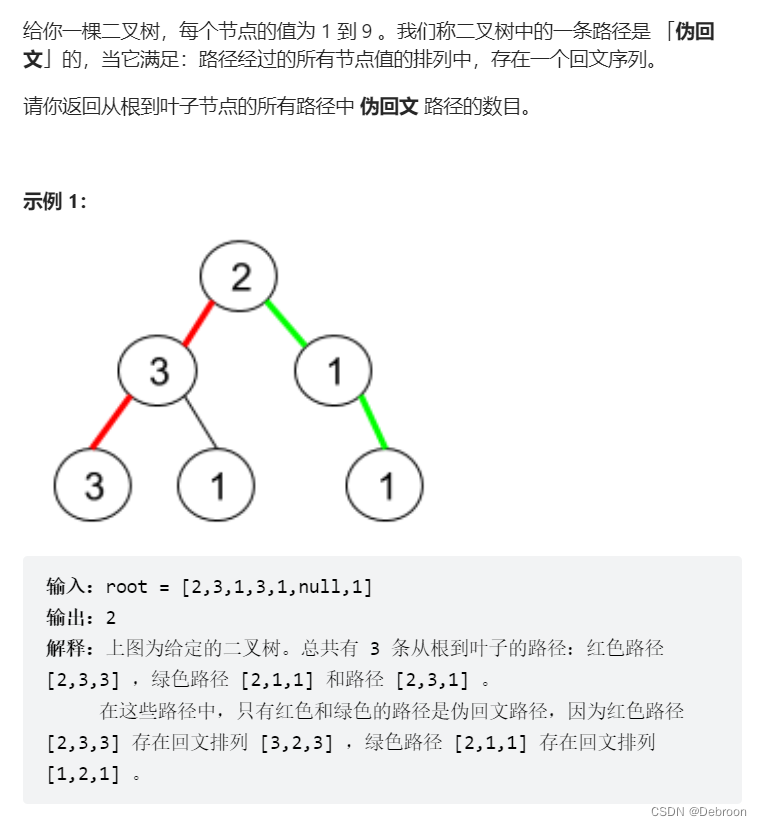
6285. 执行 K 次操作后的最大分数(327 贪心 优先队列模拟)

Math.ceil(val) 向上取整函数

    public long maxKelements(int[] nums, int k) {
        PriorityQueue<Integer> queue=new PriorityQueue<>((a,b)->(b-a));
        for(int n:nums){
            queue.add(n);
        }
        long sum=0;
        for(int i=0;i<k;i++){
            int tmp=queue.poll();
            sum+=tmp;
            queue.add((int)Math.ceil(tmp/3.0));
        }
        return sum;
    }

2536. 子矩阵元素加 1（328 二维差分前缀和）

一维原数组：8 2 6 3 1
维护一维差分数组：8 -6 4 -3 -2
差分：（存储前后变化量的）
对原数组i-j（1-3）内均加三即对差分数组i处+3，j+1处-3，处理过的差分数组变为：8 -3 4 -6 -2
求差分数组的前缀和即还原数组：8 5 9 3 1
可以看到的确是在原数组的基础上在(i，j)区间内+3

本题一维情况：
已知一维原数组
维护一维差分数组
对差分数组（记录变化量数组）的起始和结尾+1处+1
再对差分数组求前缀和，就可以还原数组，得到的在原数组基础上全部加一的数组。

本题为推广到二维的情况：
二维原数组：
维护二维差分数组（记录变化量的二维数组）：如何记录变化量？将矩阵的第[i][j]的单元格+x操作，则此矩阵求前缀和后，其右下所有部分均加一。

那如何规定指定范围的二维变化量？
从二维前缀和的角度来看，对区域左上角 +1 会对所有右下位置产生影响，那么在区域右上角的右边相邻处和左下角的下边相邻处 −1 可以消除这个影响，但是两个 −1 又会对区域右下角的右下所有位置产生影响，所以要在右下角的右下相邻处再
+1还原回来。
最后再求前缀和，即可得到最终指定范围内+x的答案。

暴力：

class Solution{
    public int[][] rangeAddQueries(int n,int[][] queries)z{
        int[][] matrix=new int[n][n];
        for(int[] query:queries){
            int x1=query[0],y1=query[1];
            int x2=query[2],y2=query[3];
            matrix[x1][y1]++;
            if(y2+1)
        }

    }
}

class Solution {
    public int[][] rangeAddQueries(int n, int[][] queries) {
        int[][] diff = new int[n + 2][n + 2];
        for (int[] query : queries) {
            int r1 = query[0] + 1, c1 = query[1] + 1;
            int r2 = query[2] + 2, c2 = query[3] + 2;
            diff[r1][c1]++;
            diff[r1][c2]--;
            diff[r2][c1]--;
            diff[r2][c2]++;
        }
        for (int i = 1; i < n + 1; i++)
            for (int j = 1; j < n + 1; j++)
                diff[i][j] = diff[i][j] + diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1];

        int[][] ans = new int[n][n];
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                ans[i][j] = diff[i + 1][j + 1];
        return ans;
    }
}

String.ValueOf()、charAt()

class Solution {
    public int alternateDigitSum(int n) {
        String num=String.valueOf(n);
        int res=0;
        for(int i=0;i<num.length();i++){
            int tmp=num.charAt(i)-'0';
            if(i%2==0){
                res+=tmp;
            }
            else{
                res-=tmp;
            }
        }
        return res;
    }
}

2545. 根据第 K 场考试的分数排序（329 lambda 二维数组自定义sort排序）

class Solution {
    public int[][] sortTheStudents(int[][] score, int k) {
        Arrays.sort(score, (a, b) -> (b[k] - a[k]));

        return score;
    }
}

异或运算

性质：0^N==N N^N=0
可解决问题类型：

• 不使用额外变量交换两个数
• 一组数据中，一种数出现奇数次，其他均出现偶数次（全部异或）
• 提出数最右侧的一 N&（(~N)+1）
• 获取最低的非0位 N&(~N)
• 一组数据中，两种数出现奇数次，其他均出现偶数次（全部异或后得到x=a^b，x!=0,x必有一位上是1。提取出x最低位1得x1，ab同位可能为0,1/1,0。令x1和数据元素相与，同为1的全部元素再次异或就可得a/b，再令x异或a/b得b/a）

6338. 猴子碰撞的方法数(快速幂、大数)

快速幂思想及实现
快速幂思想其实很简单，就是公式的转换
1、当指数是偶数时，我们可以让指数除以2，底数乘以底数
2、当指数是奇数时，我们可以将指数变为偶数

快速幂思想及实现

幂计算暴力方法：

快速幂思想就是公式的转换
1、当指数是偶数时，我们可以让指数除以2，底数乘以底数
2、当指数是奇数时，我们可以将指数变为偶数

快速幂模板

class Solution {
    public int monkeyMove(int n) {
        int mod = (int) 1e9 + 7;
        int res = qmi(2, n, mod); 
        return (res - 2 + mod) % mod;    
    }
    private int qmi(int a, int k, int q) {
        int res = 1;
        while (k != 0) {
            if ((k & 1) == 1) res =(int)((long)res * a % q); //如果指数为偶数,底数平方指数除以2，如果指数是奇数，先乘底数，再底数平方指数除以2
            k >>= 1; //指数除以2
            a = (int) ((long)a * a % q); //底数平方
        }
        return res;
    }
}