【速记】离散分布的实现算法

news2024/9/20 8:54:50

离散分布与 zipf 分布

下面的一段代码，能根据数值描述来生成对应概率的离散值：

#include <iostream>
#include <iomanip>
#include <map>
#include <random>

using namespace std;

int main()
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::discrete_distribution<> d({10, 5, 5, 10});
    std::map<int, int> map;
    for(int n=0; n<6000; ++n) {
        int randval = d(gen);
        ++map[randval];
    }
    for(int n=0; n<4; ++n) {
        std::cout << n << " generated " << std::setw(4) << map[n] << std::endl;
    }
}

执行结果：

[xiaochu.yh ~/tools/cpp] $g++ rand.cpp -std=c++17
[xiaochu.yh ~/tools/cpp] $./a.out
0 generated 2013
1 generated  923
2 generated  980
3 generated 2084
[xiaochu.yh ~/tools/cpp] $./a.out
0 generated 1985
1 generated  954
2 generated 1032
3 generated 2029

可以看到，d(gen) 可以生成0、1、2、3四个值，并且这几个值的概率大约为 0.5, 0.25, 0.25, 0.5，它正是 {10, 5, 5, 10} 的比例。

基于 discrete_distribution 类，我们通过控制它的参数，可以实现 zipf 分布：

#include <iostream>
#include <iomanip>
#include <map>
#include <random>

using namespace std;

void test_zipf()
{
    int alpha = 1;
    std::vector<double> v;
    v.reserve(26);
    for (int i = 1; i <= 26; ++i) {
      v.push_back(1.0 / pow(i, alpha));
    }
    std::random_device rd;
    std::mt19937 gen(rd());
    std::discrete_distribution<> d(v.begin(), v.end());
    std::map<int, int> map;
    for(int n=0; n<100000; ++n) {
        ++map[d(gen)];
    }
    for(int n=0; n<26; ++n) {
        std::cout << n << " generated " << std::setw(4) << map[n] << std::endl;
    }
}

输出结果如下：

[xiaochu.yh ~/tools/cpp] $g++ rand.cpp -std=c++17
[xiaochu.yh ~/tools/cpp] $./a.out
0 generated 25811
1 generated 12968
2 generated 8804
3 generated 6563
4 generated 5220
5 generated 4300
6 generated 3751
7 generated 3233
8 generated 2853
9 generated 2627
10 generated 2312
11 generated 2157
12 generated 1970
13 generated 1820
14 generated 1695
15 generated 1658
16 generated 1543
17 generated 1464
18 generated 1304
19 generated 1315
20 generated 1297
21 generated 1187
22 generated 1140
23 generated 1017
24 generated 1034
25 generated  957

用 Excel 画出一个图：
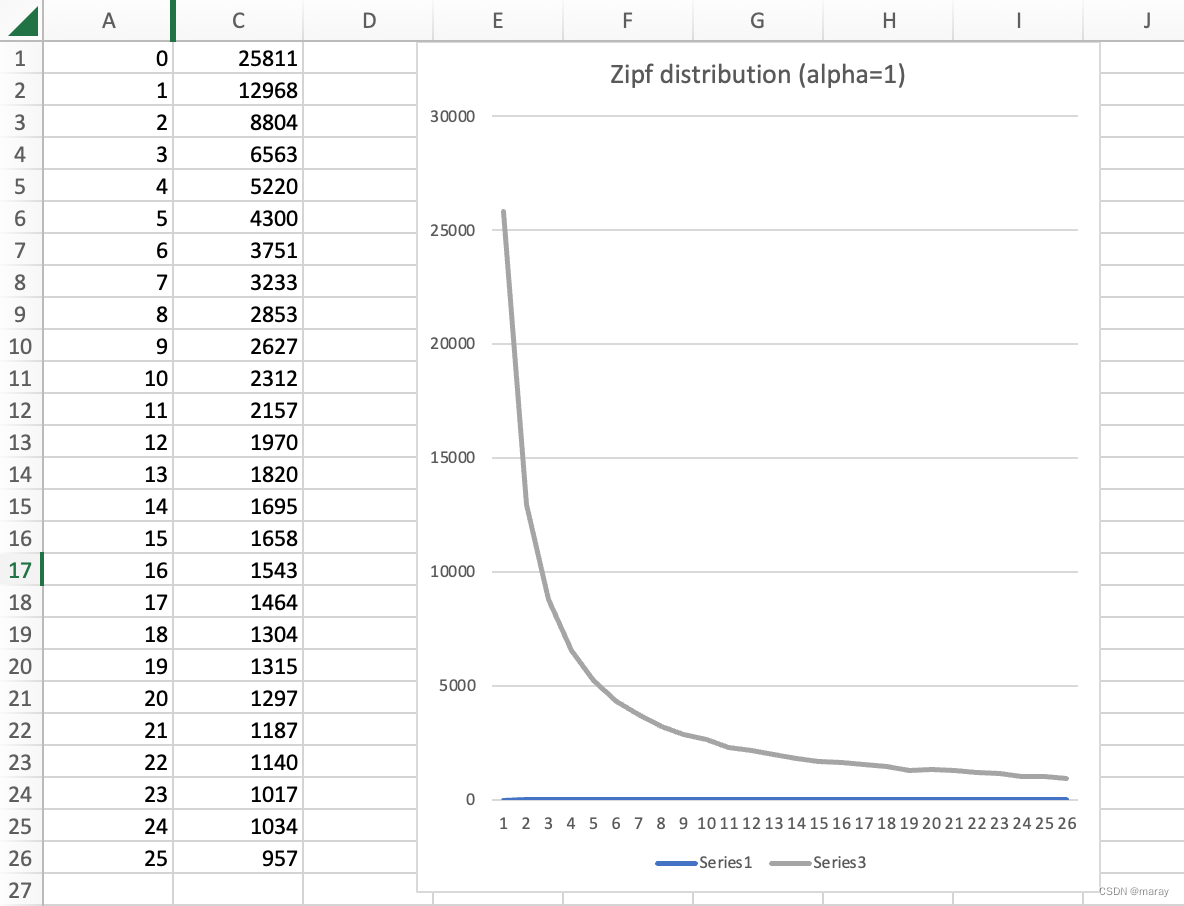
在这里插入图片描述

我们将 alpha 调整为 2，再画出一个图如下，可以看到曲线更加陡峭。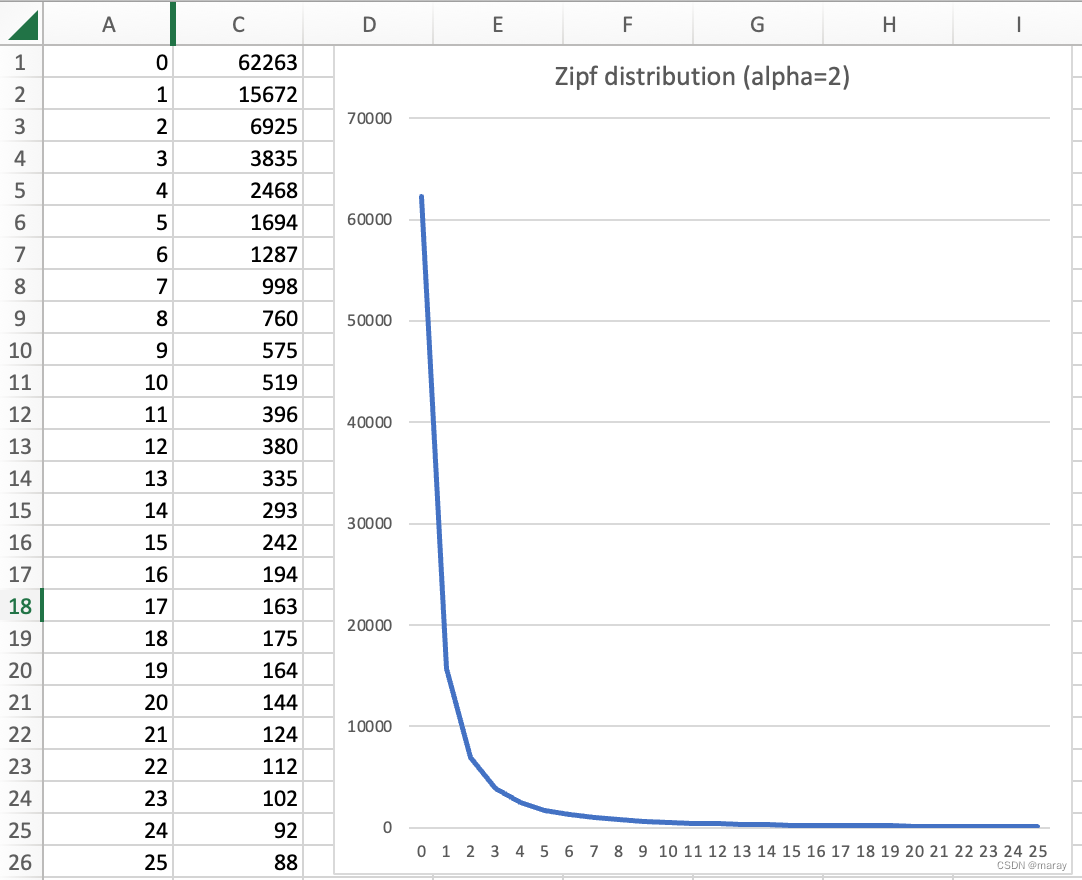在这里插入图片描述
把两个曲线放在一起对比下，可见 alpha 越大，倾斜越严重。

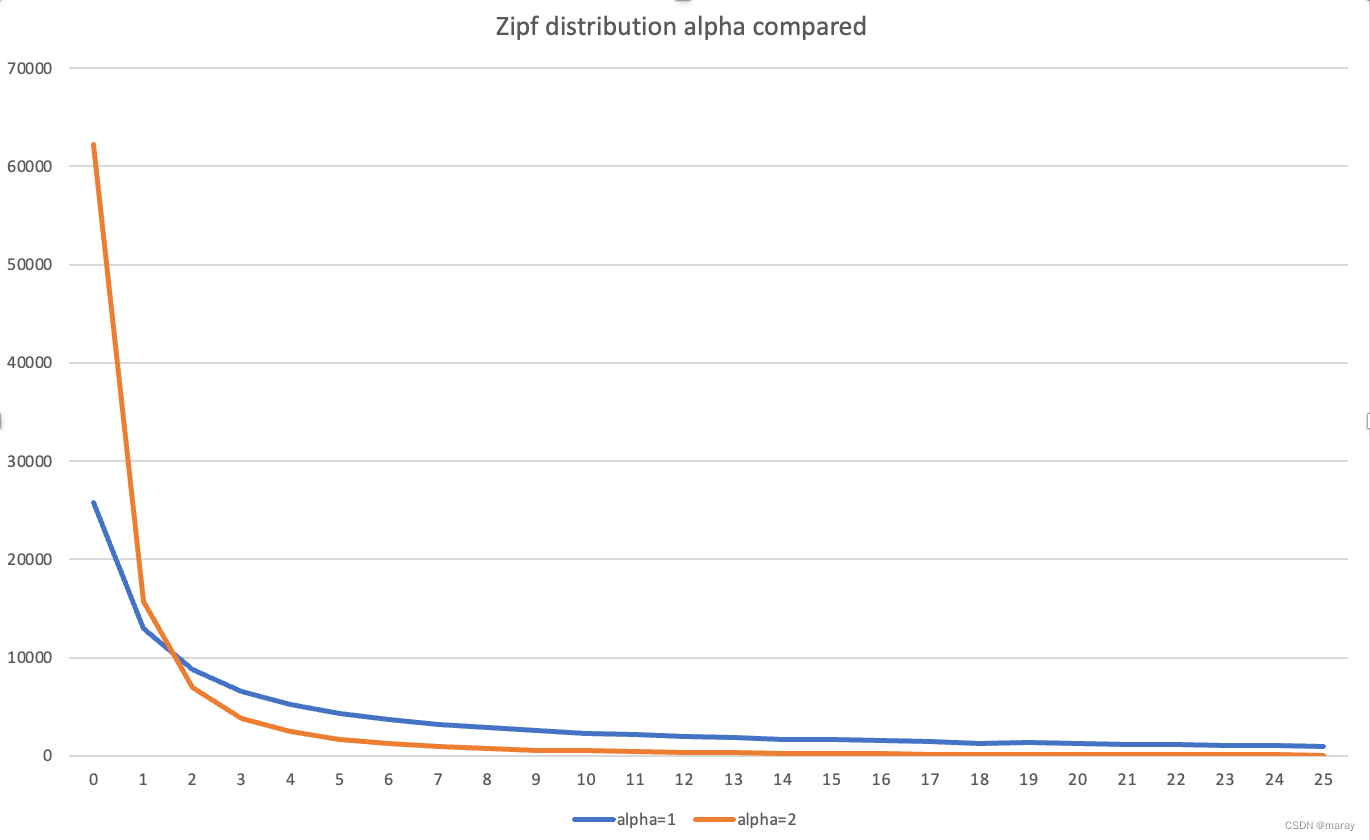
离散分布实现原理

核心逻辑分为2步

第1步是生成一个 normalized accumulative sum 数组
第2步是根据随机值在这个数组里找到一个最近的值，返回这个值的下标。

std::discrete_distribution<> d(v.begin(), v.end());

这段逻辑会完成第1步，gcc 中的实现如下：

template<typename _IntType>
    void
    discrete_distribution<_IntType>::param_type::_M_initialize()
{
    if (_M_prob.size() < 2)
	{
	  _M_prob.clear();
	  return;
	}

      const double __sum = std::accumulate(_M_prob.begin(),
					   _M_prob.end(), 0.0);
      // Now normalize the probabilites.
      __detail::__transform(_M_prob.begin(), _M_prob.end(), _M_prob.begin(),
			  std::bind2nd(std::divides<double>(), __sum));
      // Accumulate partial sums.
      _M_cp.reserve(_M_prob.size());
      std::partial_sum(_M_prob.begin(), _M_prob.end(),
		       std::back_inserter(_M_cp));
      // Make sure the last cumulative probability is one.
      _M_cp[_M_cp.size() - 1] = 1.0;
    }

这段逻辑是把从 v.begin() 到 v.end() 的值做归一化，然后求一个累加和数组。对于 {10, 5, 5, 10} 来说，求得的归一化数组就是 {0.33, 0.50, 0.66, 1}。

有了这个数组后，只需要随机生成一个 0~1之间的浮点数 f，用 f 去这个数组里找大于等于它的值，就得到一个下标。例如 f = 0.53，就找到 0.66，得到下标 2，最终输出 2。只要随机数是均匀的，那么很容易知道 f 落到 0~0.33 的概率，大于落到 0.33~0.50的概率，等等，就得到我们需要的分布。

下面是 lib 中对应的实现：

d(gen)

  template<typename _IntType>
    template<typename _UniformRandomNumberGenerator>
      typename discrete_distribution<_IntType>::result_type
      discrete_distribution<_IntType>::
      operator()(_UniformRandomNumberGenerator& __urng,
		 const param_type& __param)
{
	if (__param._M_cp.empty())
	  return result_type(0);

	__detail::_Adaptor<_UniformRandomNumberGenerator, double>
	  __aurng(__urng);

	const double __p = __aurng();
	auto __pos = std::lower_bound(__param._M_cp.begin(),
				      __param._M_cp.end(), __p);

	return __pos - __param._M_cp.begin();
}