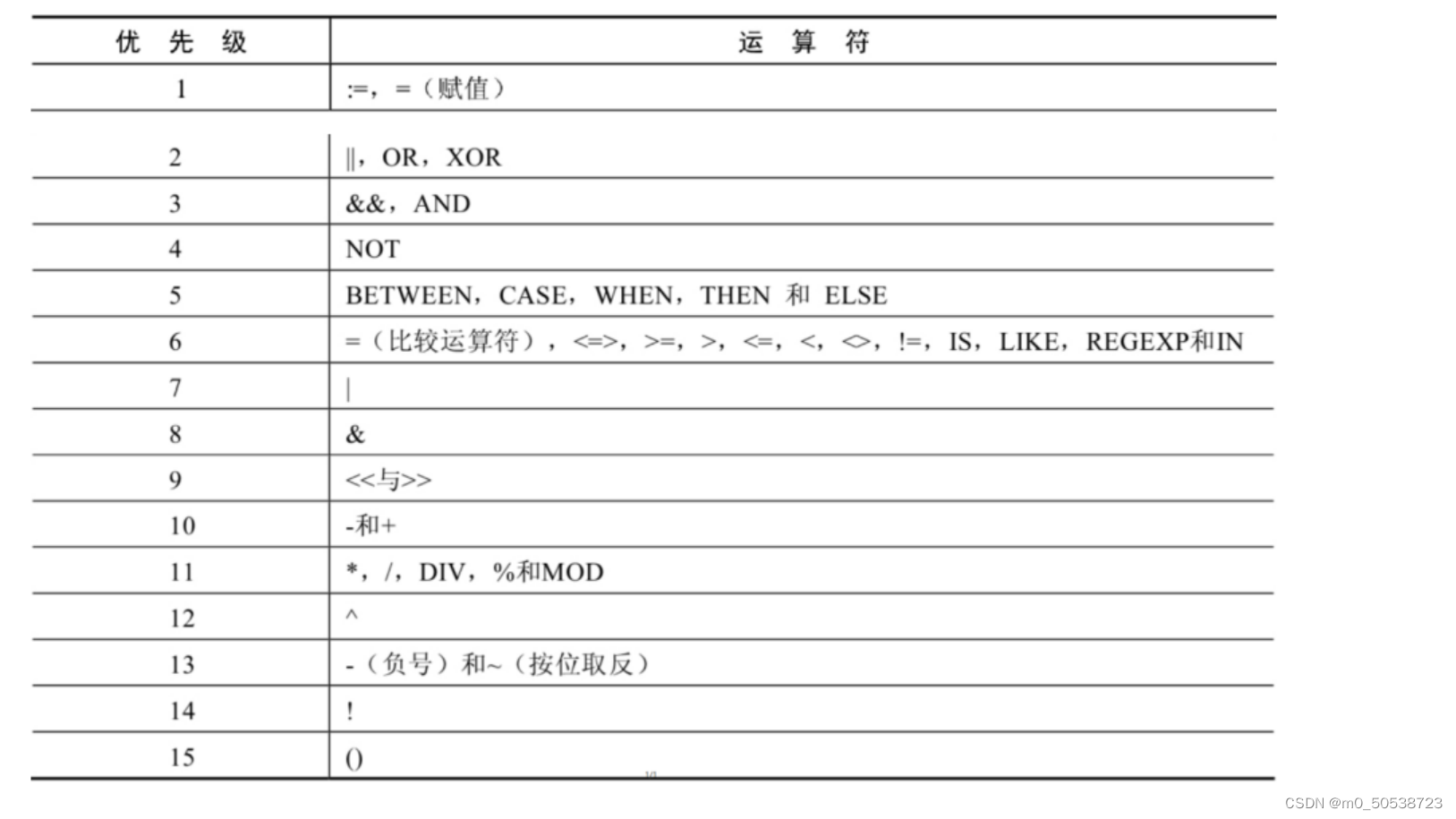
一、基础知识

 对于一个卷积层，如果希望增加输出单元的感受野，一般可以通过三种方式实现：

• 增加卷积核的大小
• 增加层数（比如两层3 × 3 的卷积可以近似一层5 × 5 卷积的效果）
• 在卷积之前进行池化操作

其中第1，2种方法会引入额外参数，第三种方法会丢失信息。

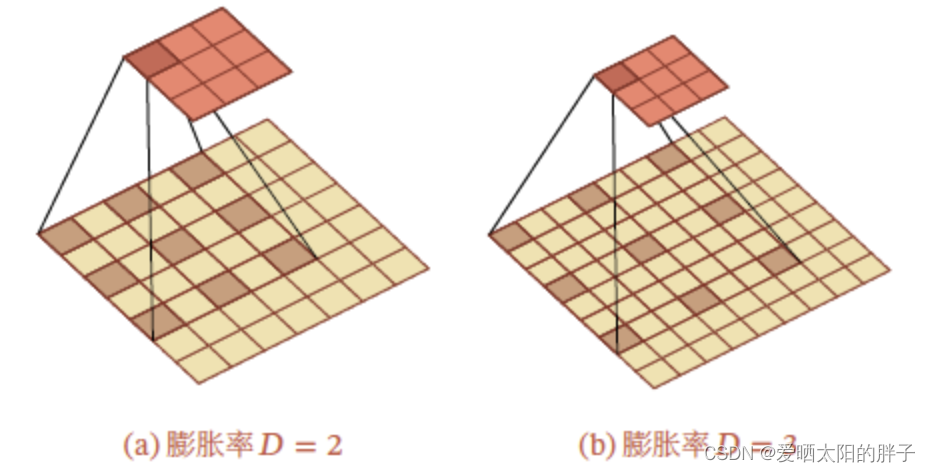
膨胀卷积是一种不增加参数数量，同时增加输出单元感受野的一种方法。空洞卷积通过给卷积核插入“空洞”来变相地增加其大小（跳过部分）．如果在卷积核的每两个元素之间插入𝐷 − 1 个空洞，卷积核的有效大小为𝐾′ = 𝐾 + (𝐾 − 1) × (𝐷 − 1)，其中𝐷 称为膨胀率（Dilation Rate）．当𝐷 = 1 时卷积核为普通的卷积核．

1.1 二维膨胀卷积

1.2 一维膨胀卷积

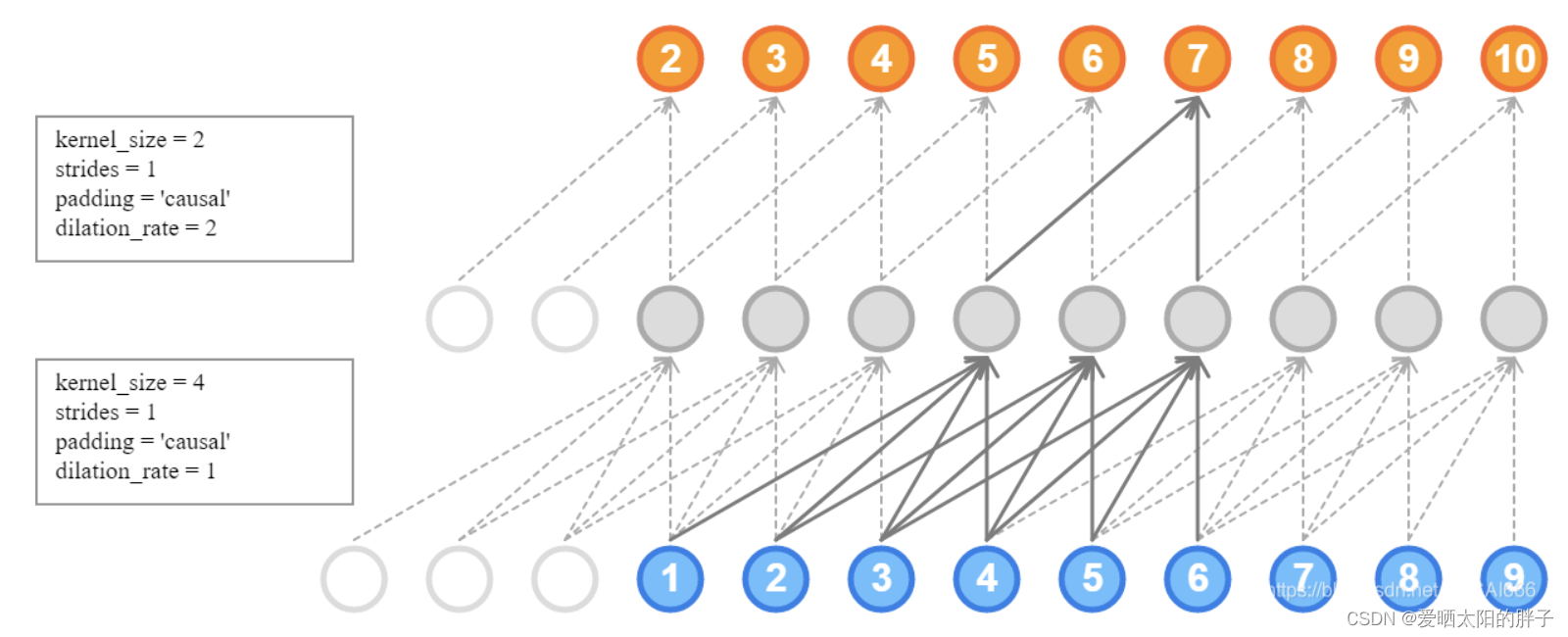
casual： 序列前补0，使得序列前面的节点也能进行卷积操作。

二、简单应用

序列处理方面，通过堆叠一维卷积层，可以实现RNN的功能，或用于缩短输入序列，将结果在作为LSTM的输入，缓解LSTM作用于长序列记忆力不足的问题。

2.1 WaveNet

图二为Aaron van den Oord和其他DeepMind研究人员在2016年提出的WaveNet的架构。它们堆叠了一维卷积层，使每一层的膨胀(dilation)率(每个神经 元输入的分散程度)加倍:第一个卷积层一次只看到两个时间步长，而下一个卷积层一次 看到四个时间步长(其接受野为四个时间步长)，下一个看到八个时间步长，以此类推。这样较低的层学习短期模式，而较高的层学习长期模式。

优势：网络可以非常有效地处理大序列。

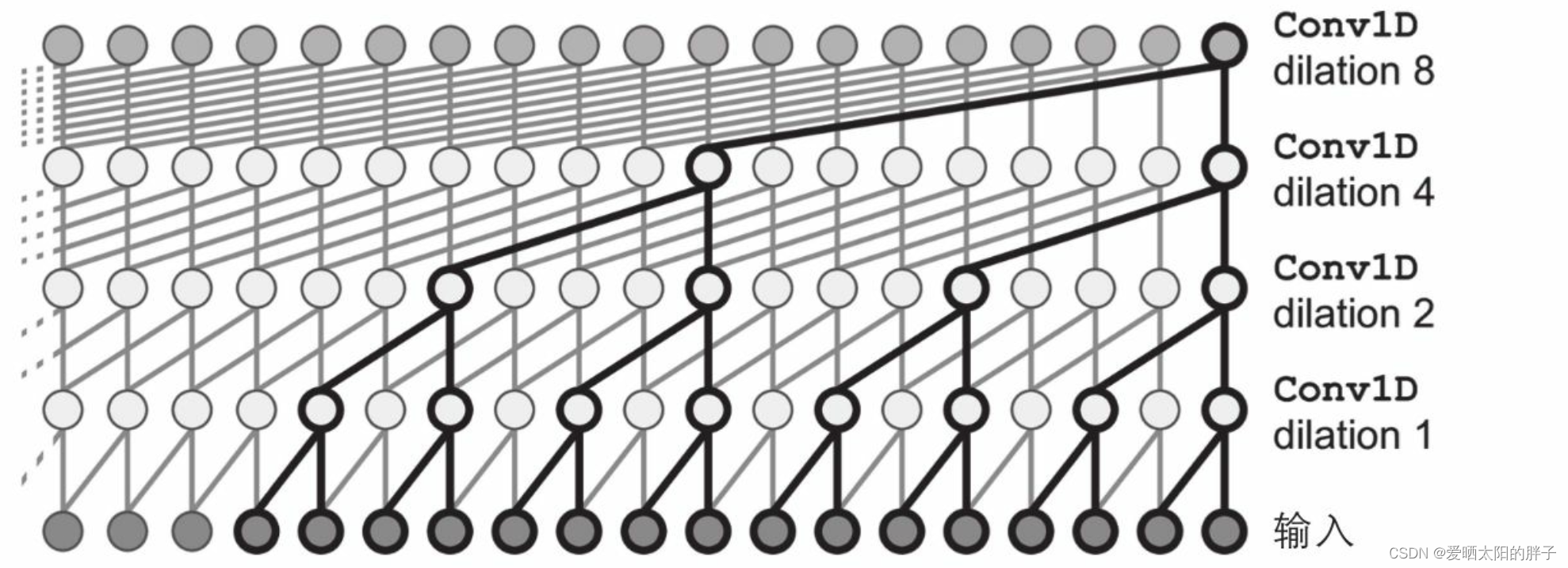
在WaveNet论文中，作者堆叠了10个卷积层，其扩散率为1、2、4、8，...， 256，512，然后又堆叠了另一组10个相同的层(扩散率也分别为1、2、4、8，...，256， 512)，然后又是另一组相同的10层。它们通过指出具有这些扩散率的10个卷积层的单个 堆栈来证明该架构的合理性，就像内核大小为1024的超高效卷积层一样工作(除了更快、 更强大且使用更少的参数之外)。

2.2.1　代码实现 

model = keras.models.Sequential()
   model.add(keras.layers.InputLayer(input_shape=[None, 1]))
   for rate in (1, 2, 4, 8，16，32，64，128，256，512) * 3:
       model.add(keras.layers.Conv1D(filters=20, kernel_size=2, padding="causal",
                                     activation="relu", dilation_rate=rate))
   model.add(keras.layers.Conv1D(filters=10, kernel_size=1))