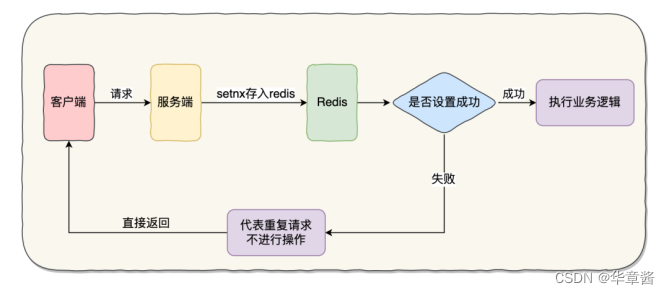
题面:

中文大意:
如果一个n个数字的序列恰好包含了1到n的所有整数,那么这个序列就被称为置换。例如,序列[3,1,4,2]。
1]和[2,1]是互换,但是[1,2,1],[0,1]和[1,3,4]不是互换。
克里斯蒂娜有一个由n个元素组成的排列组合p。她在白板上写了n次,其方式如下。
* 当她在第z次(1<i<n)写这个排列组合时,她跳过了元素p。
因此,她总共写了n个长度为n-1的序列。
例如,假设克里斯蒂娜有一个长度为4的排列组合p=[4, 2, 1, 3],那么她做了以下工作。
1. 写出序列[2, 1, 3],跳过原排列组合中的元素p; = 4。
2. 2. 写下序列[4, 1, 3],跳过原始排列中的元素py=2。
3. 3. 写了序列[4, 2, 3],跳过了原始排列中的元素p3=1。
4. 写了序列[4, 2, 1], 跳过了原始排列中的元素py = 3。
你知道写在白板上的所有n个序列,但你不知道它们的书写顺序。它们是
以任意顺序给出。从这些序列中重建原来的排列组合。
例如,如果你知道序列[4, 2, 1], [4, 2, 3], [2, 1, 3]. [4,1,3],那么原始的排列组合将是p=[4,2,1,3]。
输入
第一行输入数据包含一个整数t(I < t < 104)--测试案例的数量。
测试用例的描述如下。
每个测试案例的第一行包含一个整数n(3 < n < 100)。
接下来是7行,每行正好包含n-1个整数,描述白板上写出的一个序列。
保证所有的序列都可以从某种排列组合中得到,并且所有输入集的总和n2不超过
2-10°.
输出
对于每个测试案例,在单独的一行中输出一个排列组合p,使所给的mn个序列可以从它那里得到。
保证答案的存在,而且是唯一的一个。换句话说,对于每个测试案例,所需的排列组合肯定是存在的
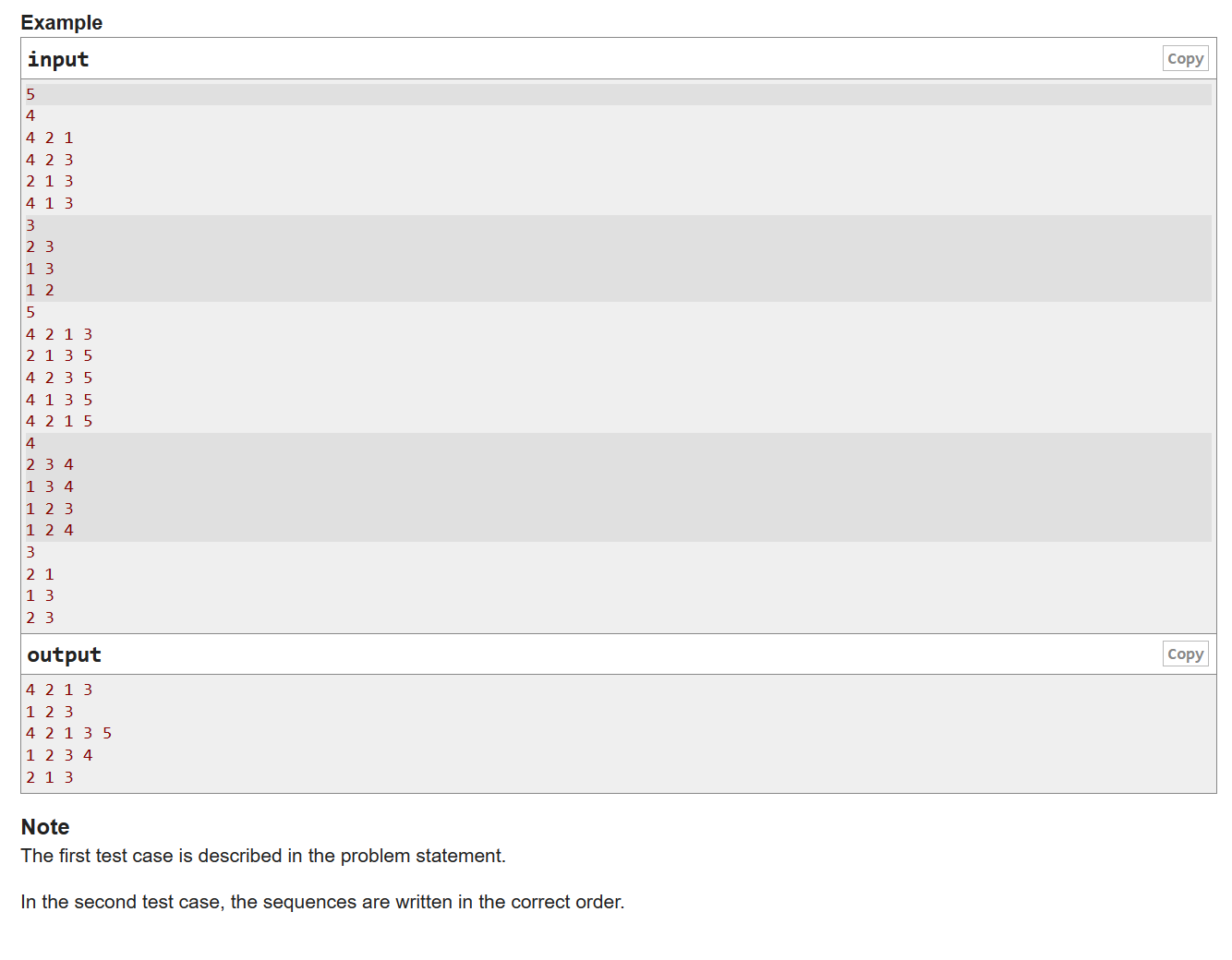
这道题感觉题目并没有很读懂,主要看样例找的规律
最终的规律是:要处理的那个n* n-1 大小的数列第一列是至关重要的,我们不难发现第一列永远是n-1个重复的数字和一个特殊的,而那个重复的数就是第一个原始数列的值,而特殊的那个数的那一排就是原始数列剩余的数
如第一个例子:
4
4 2 1
4 2 3
2 1 3
4 1 3
一开始我们知道原始数列是1 2 3 4 的一种排列
我们设原始数列为* * * * ;
我们观察
在第一列中4重复了3次
那么原始数列现在就是
4 * * * ;
然后唯一没重复的那组数据 2 1 3 即为剩下需要的
现在原始数列就能被找到了
4 2 1 3;
代码就很简单了
#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>
#include <map>
#include <stack>
#include <queue>
#include <set>
using namespace std;
typedef long long ll;
const int maxx = 1000050;
ll n, m, k, t, now, l, r, c, b , s;
const int INF = 0x3f3f3f3f;
const double pi = acos(-1.0);
int q[] = {3,1,4,1,5,9,2,6,5,3,5,8,9,7,9,3,2,3,8,4,6,2,6,4,3,3,8,3,2,7,9,5,0,2,8,8,4,1,9,7,1,6,9,3,9,9,3,7,5,1,0};
const ll mod = 1e9 + 7;
int p[225][225];
int e[225];
int ans[225];
char s1[1000100];
void check()
{
int n;
cin >> n;//输入数字终止数
for (int i = 1; i <= n; i++)//组成现实数组
{
for (int j = 1; j < n; j++)
{
cin >> p[i][j];
}
}
memset(e, 0, sizeof(e));//初始化e数组//防止下组数据影响结果
for (int i = 1; i <= n; i++)//找出第一个列里出现次数最多的,就是原始数组的第一个
{
e[p[i][1]] ++;
if (e[p[i][1]] > 1)
{
ans[1] = p[i][1];
}
}
for (int i = 1; i <= n; i++)
{
if (e[p[i][1]] == 1)//如果第一列中有一个数仅仅只出现了一次
{
for (int j = 1; j < n; j++)//那么原始数列的剩余的数就是这一排的所有数
{
ans[j + 1] = p[i][j];
}
}
}
for (int i = 1; i <= n; i++)//将排列好的数列输出
{
cout << ans[i] << " ";
}
cout << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> t;
while (t--)
{
check();
}
return 0;
}