问题描述

已知 3 个矩形的大小依次是 a_{1} \times b_{1}, a_{2} \times b_{2}a1×b1,a2×b2 和 a_{3} \times b_{3}a3×b3 。用这 3 个矩形能拼 出的所有多边形中, 边数最少可以是多少?

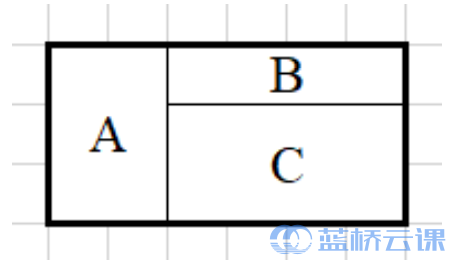
例如用 3 \times 23×2 的矩形（用 A 表示)、 4 \times 14×1 的矩形 (用 BB 表示) 和 2 \times 42×4 的矩 形（用 \mathrm{C}C 表示）可以拼出如下 4 边形。

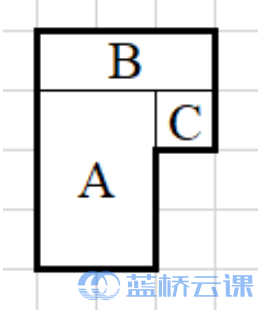
例如用 3 \times 23×2 的矩形 (用 A 表示)、 3 \times 13×1 的矩形（用 BB 表示) 和 1 \times 11×1 的矩 形（用 \mathrm{C}C 表示）可以拼出如下 6 边形。

输入格式

输入包含多组数据。

第一行包含一个整数 TT, 代表数据组数。

以下 TT 行, 每行包含 6 个整数 a_{1}, b_{1}, a_{2}, b_{2}, a_{3}, b_{3}a1,b1,a2,b2,a3,b3, 其中 a_{1}, b_{1}a1,b1 是第一个矩 形的边长, a_{2}, b_{2}a2,b2 是第二个矩形的边长, a_{3}, b_{3}a3,b3 是第三个矩形的边长。

输出格式

对于每组数据, 输出一个整数代表答案。

样例输入

2
2 3 4 1 2 4
1 2 3 4 5 6

样例输出

4
6

评测用例规模与约定

运行限制

• 最大运行时间：1s

• 最大运行内存: 512M

代码展示

import os
import sys

# 请在此输入您的代码
def check1(x1, x2, x3):

   #完全匹配，是一个四边形
  if x1>=x2 and x1>=x3:
    #当x1作为最大边时
    if x1==x2+x3 and a[2]+a[3]-x2 == a[4]+a[5]-x3:
      return True
        
  if x2>=x1 and x2>=x3:
    if x2==x1+x3 and a[0]+a[1]-x1 == a[4]+a[5]-x3:
      return True

     
  if x3>=x1 and x3>=x1:
    if x3==x1+x2 and a[0]+a[1]-x1 == a[2]+a[3]-x2:
      return True

        
def check2(x1, x2, x3):
  #完全匹配，是一个四边形
  if x1>=x2 and x1>=x3:
    if x1==x2+x3:
      return True
  if x2>=x1 and x2>=x3:
    if x2==x1+x3:
      return True

     
  if x3>=x1 and x3>=x2:
    if x3==x1+x2 :
      return True
        
        
T = int(input())
for t in range(T):
  a = list(map(int, input().split()))
  ans = 8
    
    #将三个矩形的边分别互相组合，一个矩形两条边，两种摆放情况（一横一竖）；三个矩形，共有 2x2x2 种情况。
  for i in range(0,2):#遍历下标 0， 1:
    for j in range(2,4):#遍历下标 2, 3:
      for k in range(4,6):#遍历下标 4, 5:
        x1, x2, x3 = a[i],a[j],a[k] #分别将三条边取出来，通过计算边的大小关系考虑三条表的组合的多边形，有四边形，六边形，八边形，:
        if x1==x2 and x2==x3: #三条边都相等为矩形
          ans = min(ans, 4)
                    
        if check1(x1, x2, x3):#这种四边形需要拼接才可以
          ans = min(ans, 4)
        if check2(x1, x2, x3):
          ans = min(ans, 6)
        if x1==x2 or x1==x3 or x2==x3:#当至少有两条边相等时，那么它至少为六边形:
          ans = min(ans, 6)
                    
       
  print(ans)                   
 

运行结果：

4
8