LeetCode 39. 组合总和

本题题解

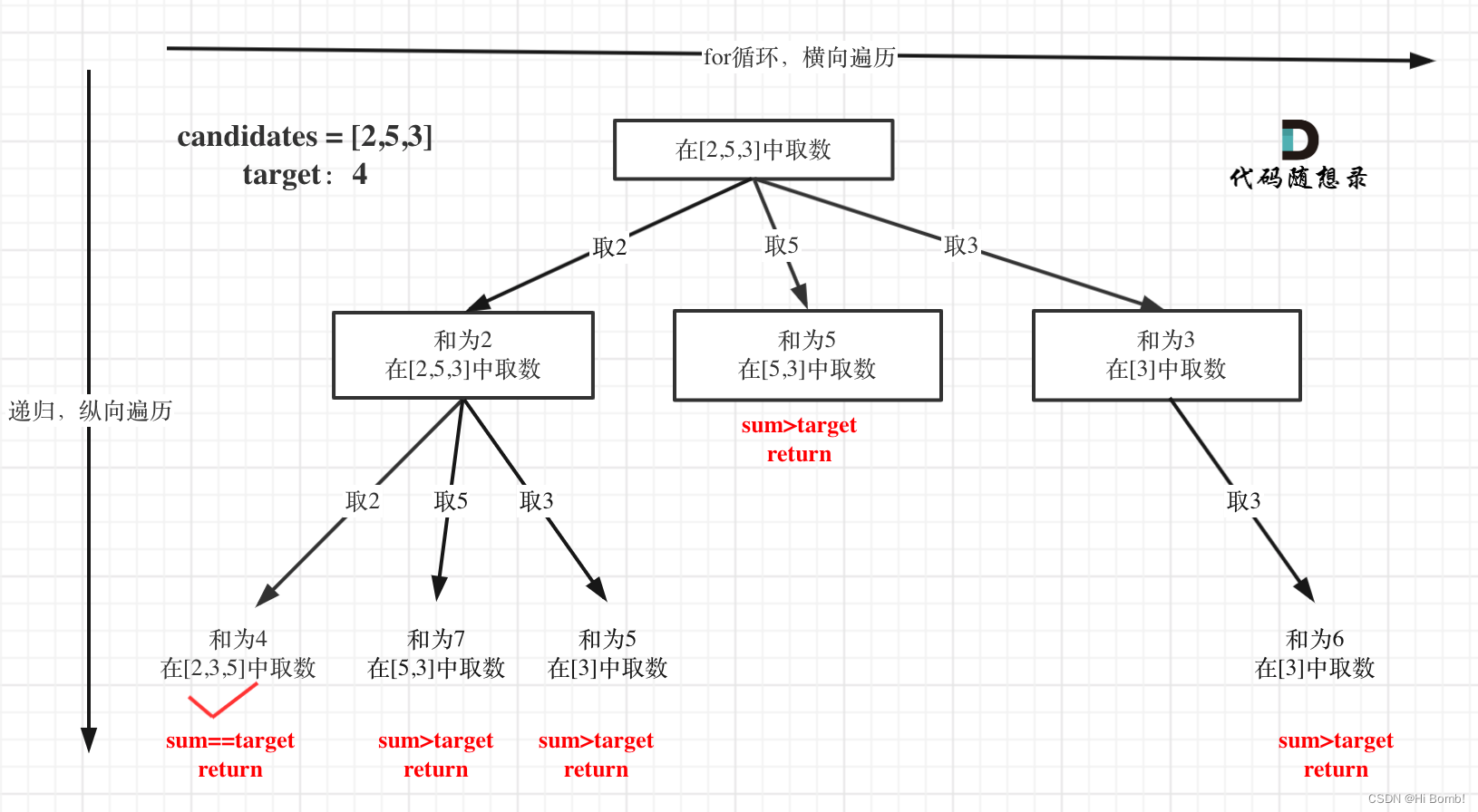
思路

根据递归三部曲来分析

递归函数参数

（这里依然是定义两个全局变量，二维数组res存放结果集，数组path存放符合条件的结果。（这两个变量可以作为函数参数传入）
首先是题目中给出的参数，集合candidates, 和目标值target。
此外我还定义了int型的sum变量来统计单一结果path里的总和，还有 idx 用来记录递归进行到哪里

递归终止条件
终止只有两种情况，
1）sum大于target和sum等于target。
2）sum等于target的时候，需要收集结果，
单层遍历

单层for循环依然是从startIndex开始，搜索candidates集合。

在这里插入图片描述

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
     List<List<Integer>> res = new ArrayList<>();
     Arrays.sort(candidates);
     backtracking( res,new ArrayList<>(),target,candidates,0,0);
     return res;
    }
    public void backtracking( List<List<Integer>> res, List<Integer> path , int target,int[] candidates,int sum,int idex)
    {
        if( sum == target)
        {
            res.add(new ArrayList<>( path));
            return;
        }
        for(int i= idex;i<candidates.length;i++)
        {
            if( sum+ candidates[i]>target)
             break;
             path.add(candidates[i]);
             backtracking(res,path,target,candidates,sum+candidates[i],i);
             path.remove(path.size()-1);
        }
    }
}

LeetCode 40.组合总和II

本题题解

思路

本题难点在于去重如何实现树层去重

返回函数参数
与39.组合总和 (opens new window)套路相同，此题还需要加一个bool型数组used，用来记录同一树枝上的元素是否使用过。
递归终止条件
与39.组合总和 (opens new window)相同，终止条件为 sum > target 和 sum == target。
单层搜索的逻辑
这里与39.组合总和 (opens new window)最大的不同就是要去重了。

如果candidates[i] == candidates[i - 1] 并且 used[i - 1] ==
false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]。

此时for循环里就应该做continue的操作。

在这里插入图片描述

class Solution {
   List<List<Integer>> res = new ArrayList<>();
   LinkedList<Integer> path = new LinkedList<>();
   int sum=0;
   boolean used[];
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {

      used = new boolean[candidates.length];
      Arrays.fill(used,false);
      Arrays.sort( candidates);
      backTracking( candidates,target,0);
      return res;
    }
    public  void backTracking(int[] candidates,int target,int StartIndex)
    {
        if(sum== target)
        {
            res.add(new ArrayList(path));
        }
        for(int i =StartIndex;i< candidates.length ;i++)
        {
            if(sum>target)
            {
                break;
            }
            if( i>0 && candidates[i]==candidates[i-1]&& !used[i-1] )
            {
                continue;
            }
            used[i]=true;
            sum +=candidates[i];
            path.add(candidates[i]);
            backTracking(candidates,target,i+1);
            used[i]=false;
            sum-= candidates[i];
            path.removeLast();
        }
    }
}

LeetCode 131.分割回文串

本题题解

思路

递归函数参数

全局变量数组path存放切割后回文的子串，二维数组result存放结果集。（这两个参数可以放到函数参数里）

本题递归函数参数还需要startIndex，因为切割过的地方，不能重复切割，和组合问题也是保持一致的。

递归函数终止条件
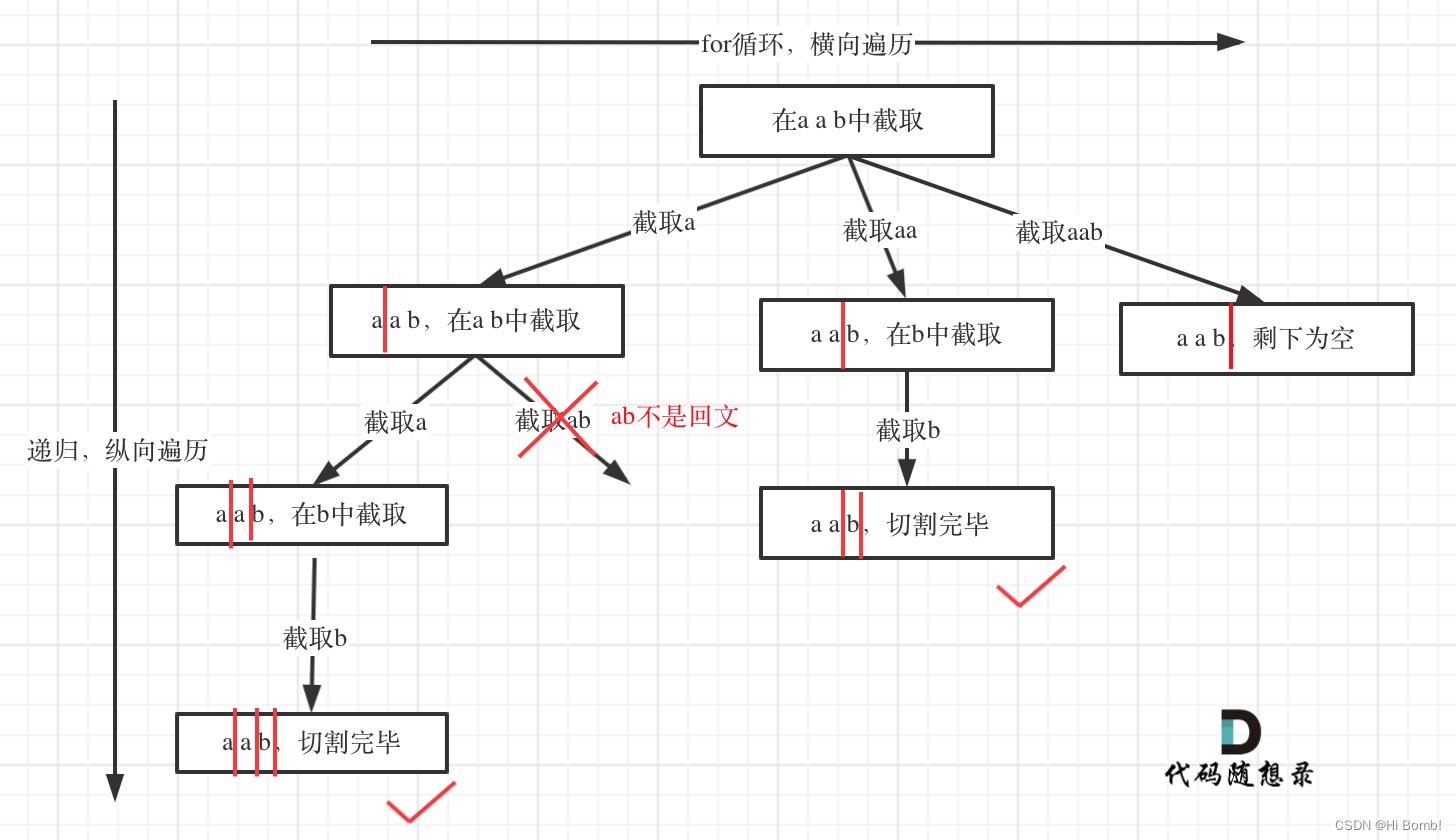
从树形结构的图中可以看出：切割线切到了字符串最后面，说明找到了一种切割方法，此时就是本层递归的终止条件。

那么在代码里什么是切割线呢？

在处理组合问题的时候，递归参数需要传入startIndex，表示下一轮递归遍历的起始位置，这个startIndex就是切割线。
从树形结构的图中可以看出：切割线切到了字符串最后面，说明找到了一种切割方法，此时就是本层递归的终止条件。

那么在代码里什么是切割线呢？

在处理组合问题的时候，递归参数需要传入startIndex，表示下一轮递归遍历的起始位置，这个startIndex就是切割线。

class Solution {
    List<List<String>> res = new ArrayList<>();
    Deque<String> deque = new   LinkedList<>();
    public List<List<String>> partition(String s) {
          backTracking(s,0);
          return res;

    }
    public void backTracking(String s,int StartIndex)
    {
        if( StartIndex>=s.length())
        {
            res.add( new ArrayList( deque));
            return;
        }
        for( int i=StartIndex;i<s.length();i++)
        {
            if( balibali(s,StartIndex,i))
            {
                String str = s.substring(StartIndex,i+1);
                deque.addLast( str);
            }
            else{
                continue;
            }
            backTracking(s,i+1);
            deque.removeLast();
        }
        
    }
    public Boolean balibali(String s,int StartIndex,int end){
        for(int i=StartIndex,j=end;i<j;i++,j--)
        {
            if( s.charAt(i)!= s.charAt(j))
            {
                return false;
            }
            
        }
        return true;
    }
}