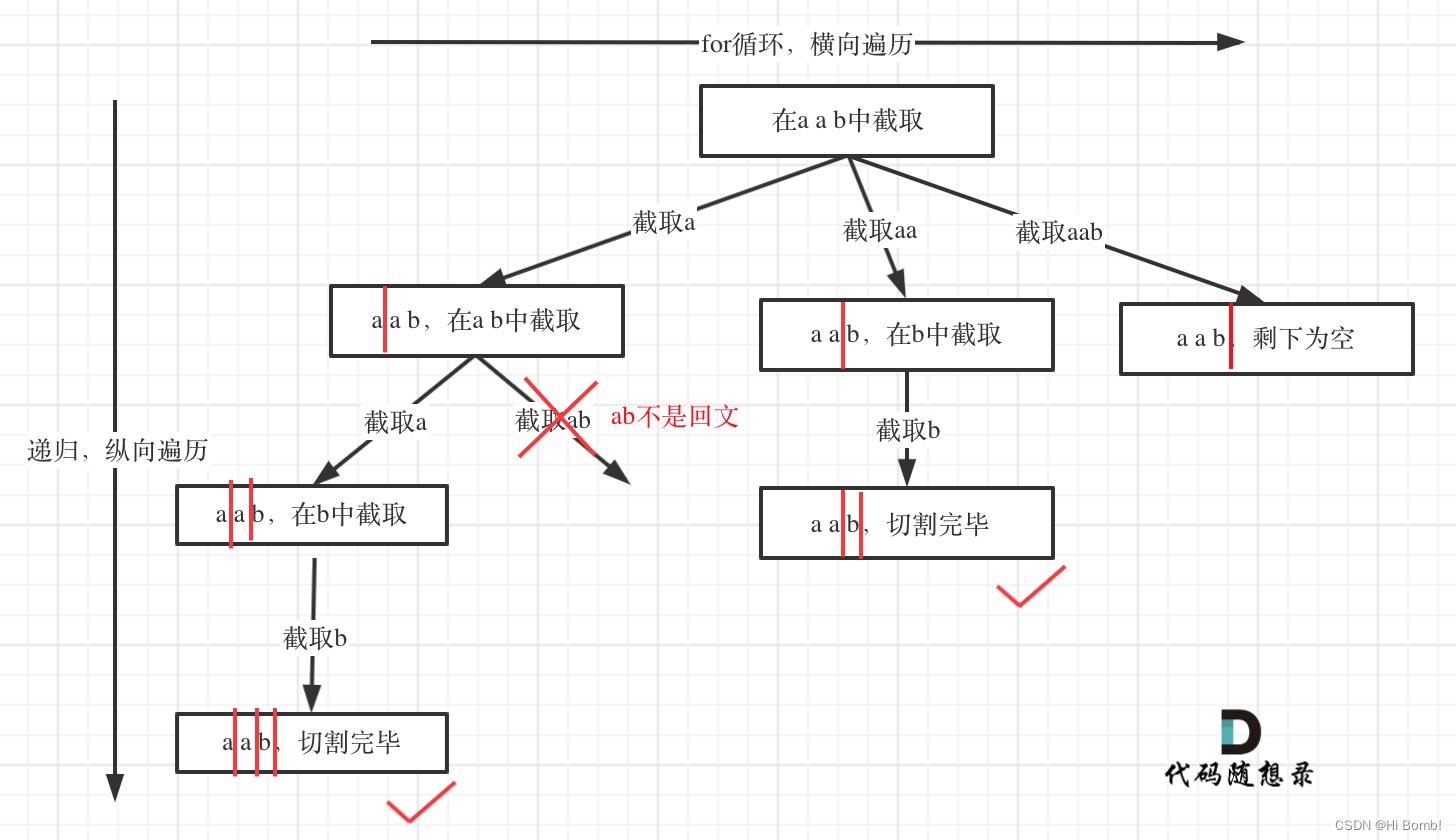
日升时奋斗,日落时自省
目录
1、选择排序
2、分割平衡字符串
3、买卖股票的最佳时机 II
4、跳跃游戏
5、钱币找零
6、多机调度问题
7、活动选择
8、无重复区间
贪心思想:顾名思义 贪 是该算法的一大特点,如何贪???
在对于问题求解时,总会做出当前看来最好的选择,也就是说不从整体最优加以考虑;他所做出的是在某种意义上的局部最优解;
那使用什么情况?
(1)贪心算法针对所有问题的整体最优可以通过一系列局部最优的选择,即贪心选择来达到,这是贪心算法可行的第一个基本要素;
(2)当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质,运用贪心策略将每一次转化都取得最优解,每一次操作都能直接对结果产生影响
基本思路:从问题的某一初始解出发一步一步地进行,根据谋个优化测度,每一步都要确保能获得局部最优解。每一步值考虑一个数据,他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起了,就不再把数据填进部分解中,直接进行枚举,或者不再添加表示算法停止
实际上,贪心算法使用的情况比较少,再使用之前选择该问题下的几个实际数据进行分析,判断即可
算法这个问题仅仅拿文字叙述太过潦草了,通过以下可以用贪心算法试题来详细理解
1、选择排序
选择排序其实就是利用贪心算法进行的,每次找到一个最小值下标,将当前序列的最小值和当前序列的开始下标进行交换;每次排序都再影响结果,以为每次排序都涉及到当前序列的最小值,整个序列从开始位置逐渐偏向有序从小到大

代码解析(附加注释解释):
public static void selectSort(int[] arr){
//外部for循环就是指当前序列 从0下标开始的当前序列 等 i++后就是 就是从1下标开始的当前序列
for(int i=0;i<arr.length;i++){
int minindex=i;
//从当前序列开始位置后找最小值
for(int j=i+1;j<arr.length;j++){
if(arr[j]<arr[minindex]){
minindex=j;
}
}
//找到当前序列的最小值之后就进行交换 当前序列的开始位置就已经确定了
if(minindex!=i){
swap(arr,minindex,i);
}
}
}
private static void swap(int[] arr, int minindex, int i) {
int tmp=arr[minindex];
arr[minindex]=arr[i];
arr[i]=tmp;
}2、分割平衡字符串
题目详细了解来源力扣 : 力扣
其实题目大体解释就是:在一个平衡字符串中: L 和 R 字符数量上是相同的,将该字符串尽可能多的分割成平衡字符串
例如: 把 LRLLLRRR 分割下来就是 LR 和 LLLRRR 这两个 既有L也有R的字符串
注:最终问的最多能分成几个平衡字符串
思路:
(1)既然说的是平衡 那就定义一个 量表示平衡 balance 表示
(2)balance什么时候最平衡 0 的时候最平衡
(3)如果遇到了L balance ++ ,如果遇到了R balance -- 一个加一个减如果平衡不就是0
(4)最后balance 处理完了, 进行判断balance当前是不是为0 也就是表示是不是一个平衡字符串
代码解析(附加注释解释):
public int balancedStringSplit(String s){
int count=0; //用来计数的
int balance=0; //记录平衡
for(int i=0;i<s.length();i++){
//处理平衡字符串
if(s.charAt(i)=='L'){
balance++;
}else if(s.charAt(i)=='R'){
balance--;
}
//平衡处理结束后 进行判定是否平衡
//每经过一次判定一次 也就没有回退操作,贪心算法步步都响应一系列局部最优
if(balance==0){
//计数 当前这段平衡字符串 是平衡的 计数加一
count++;
}
}
return count;
}3、买卖股票的最佳时机 II
题目详细了解来源力扣 : 力扣
给定一个数组 ,它的第i 个元素 是一支给定股票 第i天的价格
设计一个算法来计算你所能获得的最大利润,你可以尽可能地完成更多的交易(可以多次买卖一支股票)
注:手里只能有一支股票 ,也就是你买了一支股票就需要先卖掉,才能,买下一支股票

代码解析(附加注释):
public static int maxProfit(int[] prices){
int result=0; //用来记录当前利润收入
// 当前手上有一支股票 所以 i从 1下标开始
for(int i=1 ;i<prices.length;i++){
//计算今天和明天股票的利润
int curProfit=prices[i]-prices[i-1];
//如果股票的利润是正数那就记录下来 贪心算法 每次买卖股票最优就是有利润
if(curProfit>0){
result+=curProfit;
}
}
return result;
}4、跳跃游戏
题目详细了解来源力扣 :力扣
(1)给定一个非负整数数组,你最初位于数组的第一个位置
(2)数组中的每个元素代表你在该位置可以跳跃的最大长度
(3)判断你是否能够到达最后一个位置

代码解析(附加注释解释):
public boolean canJump(int[] nums){
int n=nums.length; //计算数组元素个数 用于判定跳跃是否能跳到
int rightmost=0; //此处是记录 跳跃最大能跳到右侧的哪里
for(int i=0;i<nums.length;i++){
//当前锁在最大值不能小于当前下标了, 否则说明最大值只能跳跃到当前下标或者跳跃不到当前位置
if(i<=rightmost){
//贪心判定 每次都是 只保留最大跳跃的位置
rightmost=Math.max(rightmost,i+nums[i]);
//直到第一个最大跳跃位置能当前数组最后的位置
if(rightmost<=n-1){
return true;
}
}
}
return false;
}5、钱币找零
假设1元、2元、5元、10元、20元、50元、100元的纸币分别有c0, c1, c2, c3, c4, c5, c6张。现在要用这些钱来支付K元,至少要用多少张纸币?
例如:将96转化为零钱
贪心思想:
(1)从最大的币值开始 也就是 100币值 大于当前值 向后缩减
(2)进行下一个币值的比较如果小于当前值,将当前值最大处理(图片解释)
(3)最终判定96是否能全部被置换,如果不能返回NO 如果能返回最少几张钱币

代码解析(附加注释):
public static void main(String[] args) {
//设置 以下面值以及对应的数量
int[][] moneyCount={{1,3},{2,1},{5,4},{10,3},{20,0},{50,1},{100,10}};
//输入你要 置换的面值
Scanner scanner=new Scanner(System.in);
int money;
System.out.println("请输入要支付的钱");
money=scanner.nextInt();
//进行置换处理
int result=solve(money,moneyCount);
//判断如果返回值不是 -1 那说明能置换成功
if(result!=-1){
System.out.println(result);
}else{
System.out.println("No");
}
}
private static int solve(int money, int[][] moneyCount) {
int num=0;
//贪心 思想
//从面值大 钱币开始 为了能够以最少的钱币数量 置换结束
for(int i=moneyCount.length-1;i>=0;i--){
//求需要置换的钱 和 能中和掉多少张当前面值 取最小值
//一个是 要满足 当前的钱 能 容纳下
//另一个 要满足 面值数量 是否够
int c=Math.min(money/moneyCount[i][0],moneyCount[i][1]);
//将当前的钱 - 最大数量的面值
money=money-c*moneyCount[i][0];
//加上需要消耗的面值数量
num+=c;
}
//如果不能找开 钱就还有剩余 所以返回-1
if(money>0){
return -1 ;
}
//如果能找开, 返回钱币数量
return num;
}6、多机调度问题
某工厂有n个独立的作业,由m台相同的机器进行加工处理,作业i所需的加工时间ti,任何作业在被处理时不能中断,也不能进行拆分处理。现厂长请你给写一个程序:算出n个作业由m台机器加工处理的最短时间
此处:贪心思维就在于处理最大任务时间,将任务时间从降序分配给时间任务最小的机器
题目解析:
(1)首先需要输入机器数 ,一台机器处理一个任务时间
(2)如果任务数大于机器数:就是将处理最短时间任务的机器,将其他任务时间给当前机器
(3)重复以上操作(以下图解)
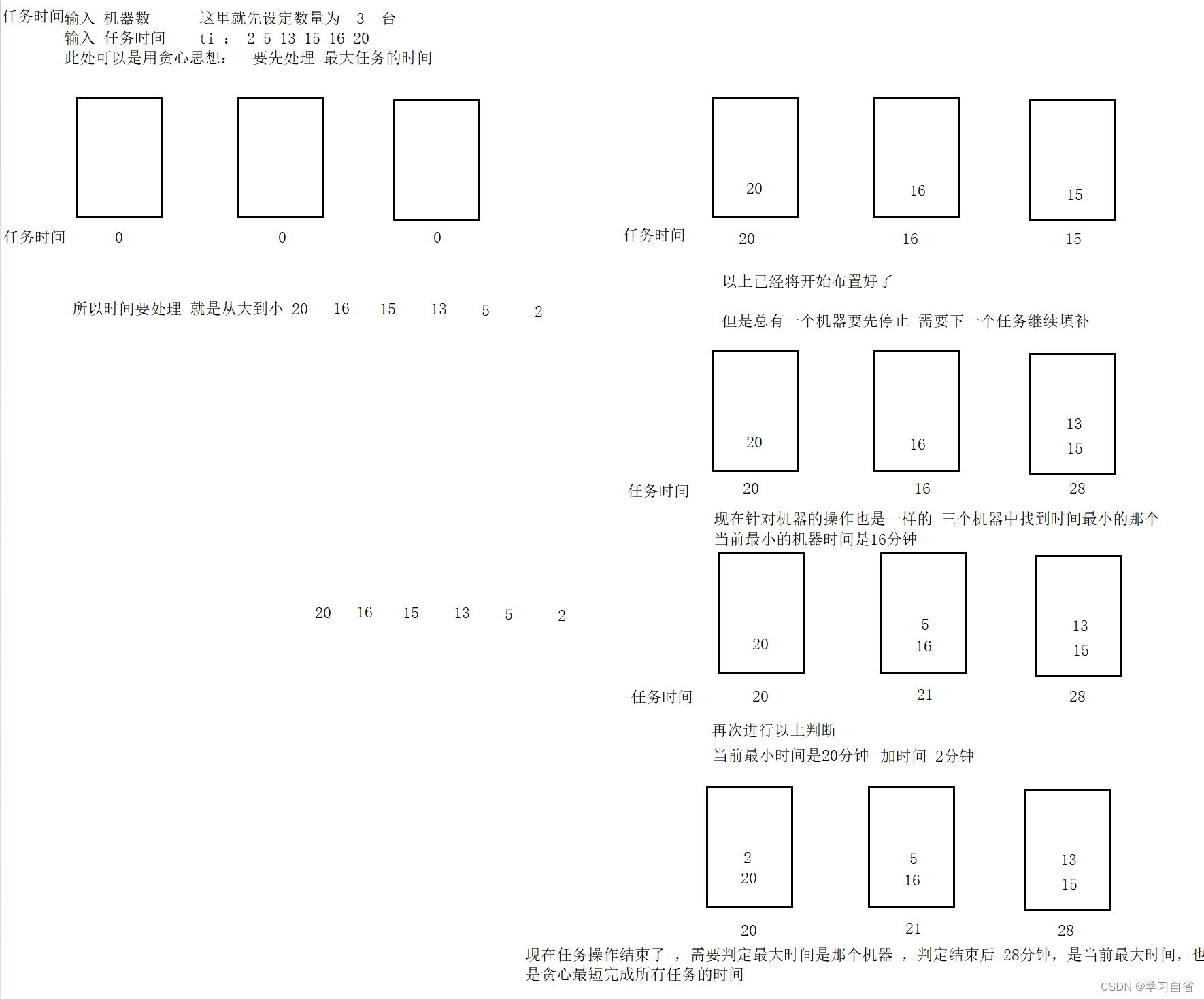
代码解析(附加注释):
以下代码有点长, 图解是思路解释,先通好思路,然后看以下代码,注释详细
public class MultiMachineTest {
public static void main(String[] args) {
int n,m;
System.out.println("请输入作业数和机器数");
Scanner scanner=new Scanner(System.in);
//输入任务数量
n=scanner.nextInt();
//机器数量
m=scanner.nextInt();
//创建一个针对任务数量的数组 一会用于存放对应的任务的时间
Integer[] works=new Integer[n];
//以数组创建m个机器
Integer[] machines=new Integer[m];
//给每个任务都需要赋值一定的任务时间
for(int i=0;i<n;i++){
works[i]=scanner.nextInt();
}
//将所有机器处理
System.out.println(greedStrateg(works,machines));
}
private static int greedStrateg(Integer[] works, Integer[] machines) {
//首先 给定的时间肯定不是有序的 所以需要对当前传来数组进行排序 还是降序排序
//贪心算法 从最大时间开始
int minimaTime= machines.length; //记录最短时间
int workNum=works.length; //机器数量
Arrays.sort(works,new myComparator());
//作业数如果小于机器数 ,直接返回最大的作业时间 其实也就是最短时间
if(workNum<minimaTime){
return works[0];
}else{
//作业数大于机器数的情况
for(int i=0;i<works.length;i++){
//选择最小的机器 任务时间加上
int flag=0;
//首先假设用第一个机器处理 ,也就是临时机器
int tmp=machines[flag];
//从剩余的机器中找运行时间最短的机器,进行加任下一个任务
for(int j=1;j<machines.length;j++){
//找最小值 进行加任务 有点像插入排序
if(tmp>machines[j]){
flag=j;
//记录下来
tmp=machines[j];
}
}
//将当前作业交给最小的机器执行
machines[flag]+=works[i];
}
//从所有机器中选出最后执行完成作业的机器 刚刚图解再最后找的是当前序列的最大值
minimaTime=findMax(machines);
return minimaTime;
}
}
private static int findMax(Integer[] machines) {
//先假设机器的 为最小值
int ret=machines[0];
//进行操作比对操作
for(int cur:machines){
//找到当前序列的最大值
if(ret<cur){
ret=cur;
}
}
//返回最大值 也是所有机器运行的最短时间
return ret;
}
}
class myComparator implements Comparator<Integer> {
@Override
public int compare(Integer a, Integer b) {
return b-a;
}
//按作业时间从大到小排序
}
7、活动选择
有n个需要在同一天使用同一个教室的活动a1, a2, …, an,教室同一时刻只能由一个活动使用。每个活动a[i]都有一个开始时间s[i]和结束时间f[i]。一旦被选择后,活动a[i]就占据半开时间([s[i],f[i])。如果([s[i],f[i])和([s[j],f[j])互不重叠,a[i]和a[j]两个活动就可以被安排在这一天。求使得尽量多的活动能不冲突的举行的最大数量
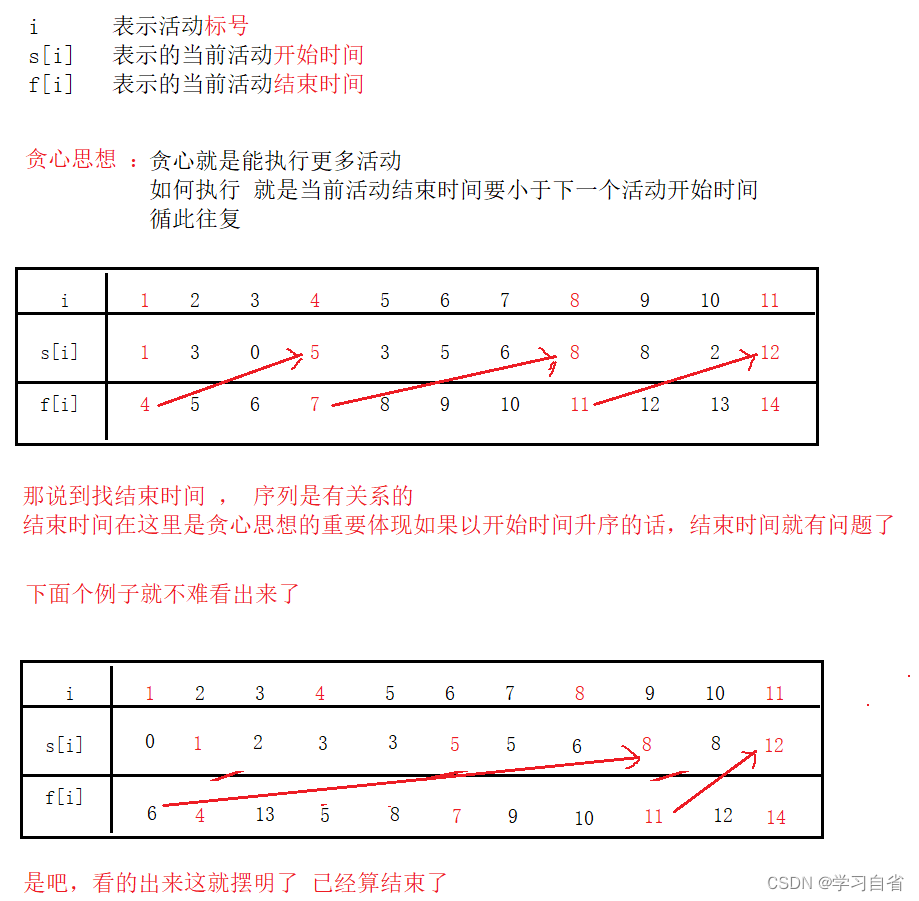
代码解析(附加注释):
public class ActivitySelection {
public static void main(String[] args) {
Scanner scanner=new Scanner(System.in);
int number=scanner.nextInt();
//活动 使用二维数组表示 行表示序号 列就表示0标 代表 开始时间和1标 代表 结束时间
int[][] act=new int[number][2];
int idx=0;
for(int i=0;i<act.length;i++){
act[i][0]=scanner.nextInt(); //表示开始时间
act[i][1]= scanner.nextInt(); //表示结束时间
}
//以结束时间排序 贪心就在于找结束时间 主要就是找
Arrays.sort(act,new MyComparator());
//这就是 活动选择
int ret=greedyActivitySelector(act);
System.out.println(ret);
}
public static int greedyActivitySelector(int[][] act){
//num表示活动个数 本身就是1个 所以num=1 i表示当前活动
int num=1,i=0;
//j=1表示下一个活动
for(int j=1;j<act.length;j++){
//表示下一个活动开始时间 大于 当前活动结束时间
if(act[j][0]>=act[i][1]){
//进行比对成功后 下一个活动也成了当前活动
i=j;
//每能进行一次比对 活动个数加一
num++;
}
}
return num;
}
}
class MyComparator implements Comparator<int[]>{
//以 活动结束时间 进行排序
@Override
public int compare(int[] o1, int[] o2) {
return o1[1]-o2[1];
}
}8、无重复区间
题目详细了解来源力扣 :力扣
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠
注意:可以认为区间的终点总是大于它的起点,区间[1,2]和[2,3]的边界相互“接触”,但没有相互重叠

代码解释(附加注释):
class MyComparatorNow implements Comparator<int[]>{
@Override
public int compare(int[] o1, int[] o2) {
//用来计算 前者排序
return o1[0]-o2[0];
}
}
public int eraseOverlapIntervals(int[][] intervals){
if(intervals.length==0){
return 0;
}
//此处进行排序 排序的是区间的开始位置 为以下的操作做准备
Arrays.sort(intervals,new MyComparatorNow());
int end=intervals[0][0]; //把当前位置作为准备的区间
int prev=0; //前一个区间
int count=0; //用来计数 要移除的区间
for(int i=1;i<intervals.length;i++){
//对比的是 前一个区间的末尾位置 大于 后一个区间的初识位置
//第二种情况
if(intervals[prev][1]>intervals[i][0]){
//当前范围内是大于后一个区间的初识位置,还要判断是否大于后一个区间的末尾位置
//前一个区间包含了后一个区间,那就说明了出现重复区间了
//第三种情况
if(intervals[prev][1]>intervals[i][1]){
//此处是包含后一个区间了 为了减少前一个大区间的影响,前一个大区间会被移除,留下后一个小区间
prev=i;
}
//当前无论是前一个区间还是后一个区间
//因为第二种情况 包含了 第三种情况 都是要进行移除数量+1
count++;
}else{//第一种情况
//如果 前一个区间的末尾值 小于 后一个区间的初始值
//那就将下一个区间作为对比区间 当前不是重叠区间
prev=i;
}
}
//返回区间个数
return count;
}总结:贪心算法针对最多最少类问题,可以进行一系列局部最优后完成整体最优,如果实际上问题,个例问题过多不就成了全部枚举,贪心算法是尽可能一系列局部最优,个别枚举。