笔者在源码笔记1之中分析过ClickHouse的聚合函数的实现,但是对于各个接口函数的实际如何共同工作的源码,回头看并没有那么明晰,主要原因是没有结合Aggregator的类来一起分析聚合函数的是如果工作起来的。所以决定重新再完成一篇聚合函数的源码梳理的文章,帮助大家进一步的理解ClickHouse之中聚合函数的工作原理。 本系列文章的源码分析基于ClickHouse v19.16.2.2的版本。
1.IAggregateFunction接口梳理
话不多说,直接上代码,笔者这里会将所有聚合函数的核心接口代码全部列出,一一梳理各个部分:
构造函数
IAggregateFunction(const DataTypes & argument_types_, const Array & parameters_)
: argument_types(argument_types_), parameters(parameters_) {}复制
上面的代码实现了IAggregateFunction接口的构造函数,初始化了该接口的两个成员变量:
argument_type:函数的参数类型,比如函数select sum(a), sum(b), c from test group by c, 这里a,b分别是UInt16类型与Double类型,那么这个sum(a)与sum(b)的参数就不同。parameters: 参数,实际类型为std::vector<Field>。它代表着函数的除了数据的输入参数之外的其他参数。比如聚合函数topk,其中需要传入的k的值就在parameters之中。
内存分配接口
在Clickhouse的聚合执行过程之中,所有的聚合函数都是通过列来进行的。而这里有两个重要的问题:
- 列内存从哪里分配
- 分配的内存结构,长度是如何的 笔者在梳理下面代码的过程之中给出解答,
/** Create empty data for aggregation with `placement new` at the specified location.
* You will have to destroy them using the `destroy` method.
*/
virtual void create(AggregateDataPtr place) const = 0;
/// Delete data for aggregation.
virtual void destroy(AggregateDataPtr place) const noexcept = 0;复制
IAggregateFunction定义的两个接口create与destory接口完成了内存结构与长度的确定,这里可能描述的不是很明白,这里了解Doris聚合实现的同学可以这样理解。create函数本身就是完成了Doris聚合函数之中init函数所完成的工作。这里通过子类IAggregateFunctionDataHelper的实现代码来进一步理解它做了什么事情:
void create(AggregateDataPtr place) const override
{
new (place) Data;
}
void destroy(AggregateDataPtr place) const noexcept override
{
data(place).~Data();
}复制
这部分代码很简单,Data就是模板派生的类型,然后通过placement new与placement delete的方式完成了Data类型的构造与析构。而这个Data类型就是聚合函数存储中间结果的类型,比如sum的聚合函数的派生类型是类AggregateFunctionSumData的内存结构,它不仅包含了聚合结果的数据sum同时也包含了一组进行聚合计算的函数接口add,merge等:
template <typename T>
struct AggregateFunctionSumData
{
T sum{};
void add(T value)
{
sum += value;
}
void merge(const AggregateFunctionSumData & rhs)
{
sum += rhs.sum;
}
T get() const
{
return sum;
}
};复制
这里就是通过create与destory函数调用AggregateFunctionSumData的构造函数与析构函数。而问题又绕回第一个问题了,这部分内存是在哪里分配的呢?
aggregate_data = aggregates_pool->alignedAlloc(total_size_of_aggregate_states, align_aggregate_states);
createAggregateStates(aggregate_data);复制
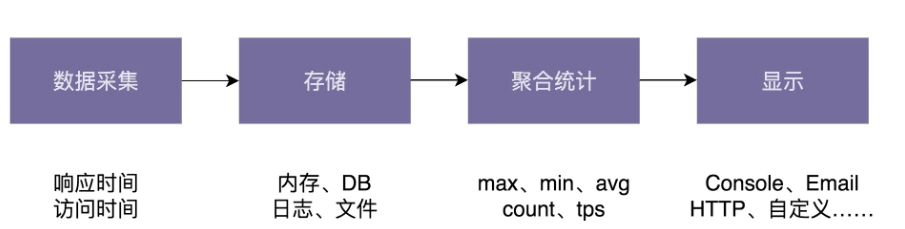
在进行聚合运算时,通过Aggregator之中的内存池进行单行所有的聚合函数的数据结果的内存分配。并且调用createAggregateStates依次调用各个聚合函数的create方法进行构造函数的调用。这部分可能有些难理解,我们接着看下面的流程图,来更好的帮助理解:

create函数在聚合的流程之中的作用
通过上述流程图可以看到,create这部分就是在构造聚合hash表时,进行内存初始化工作的,而这部分内存不仅仅包含了聚合函数的结果数据,还包含了对应聚合算子的函数指针。后文我们分析计算接口的时候也会同样看到。接下来,来看destory就很容易理解了,就是在聚合计算结束或取消时,遍历hash表,并调用析构函数对hash表中存储的Data类型调用析构函数,而最终的内存伴随着aggregates_pool内存池的析构而同时释放。
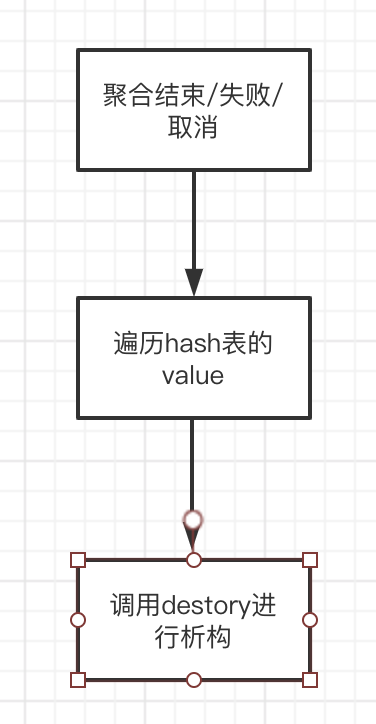
detory函数在聚合流程之中的作用
函数计算接口
接下来就是聚合函数最核心的部分,聚合函数的计算。
/** Adds a value into aggregation data on which place points to.
* columns points to columns containing arguments of aggregation function.
* row_num is number of row which should be added.
* Additional parameter arena should be used instead of standard memory allocator if the addition requires memory allocation.
*/
virtual void add(AggregateDataPtr place, const IColumn ** columns, size_t row_num, Arena * arena) const = 0;
/// Merges state (on which place points to) with other state of current aggregation function.
virtual void merge(AggregateDataPtr place, ConstAggregateDataPtr rhs, Arena * arena) const = 0;
/** Contains a loop with calls to "add" function. You can collect arguments into array "places"
* and do a single call to "addBatch" for devirtualization and inlining.
*/
virtual void addBatch(size_t batch_size, AggregateDataPtr * places, size_t place_offset, const IColumn ** columns, Arena * arena) const = 0;复制
IAggregateFunction定义的3个接口:
add函数将对应AggregateDataPtr指针之中数据取出,与列columns中的第row_num的数据进行对应的聚合计算。addBatch函数:这是函数也是非常重要的,虽然它仅仅实现了一个for循环调用add函数。它通过这样的方式来减少虚函数的调用次数,并且增加了编译器内联的概率,同样,它实现了高效的向量化。merge函数:将两个聚合结果进行合并的函数,通常用在并发执行聚合函数的过程之中,需要将对应的聚合结果进行合并。
这里的两个函数类似Doris之中聚合函数的update与merge。接下来我们看它是如何完成工作的。
首先看聚合节点Aggregetor是如何调用addBatch函数:
/// Add values to the aggregate functions.
for (AggregateFunctionInstruction * inst = aggregate_instructions; inst->that; ++inst)
inst->that->addBatch(rows, places.data(), inst->state_offset, inst->arguments, aggregates_pool);复制
这里依次遍历AggregateFunction,并调用addBatch接口。而addBatch接口就是一行行的遍历列,将参数列inst->arguments与上文提到create函数构造的聚合数据结构的两列列数据进行聚合计算:
void addBatch(size_t batch_size, AggregateDataPtr * places, size_t place_offset, const IColumn ** columns, Arena * arena) const override
{
for (size_t i = 0; i < batch_size; ++i)
static_cast<const Derived *>(this)->add(places[i] + place_offset, columns, i, arena);
}复制
这里还是调用了add函数,我们通过AggregateFunctionSum作为子类来具体看一下add的具体实现:
void add(AggregateDataPtr place, const IColumn ** columns, size_t row_num, Arena *) const override
{
const auto & column = static_cast<const ColVecType &>(*columns[0]);
this->data(place).add(column.getData()[row_num]);
}复制
这里其实还是调用上文提到的AggregateFunctionSumData的内存结构的add函数完成聚合计算。而这个add函数就是一个简单的相加逻辑,这样就完成了简单的一次聚合运算。
void add(T value)
{
sum += value;
}复制
而merge函数的实现逻辑类似于add函数,这里就不展开再次分析了。
函数结果输出接口
最后就是聚合函数结果输出接口,将聚合计算的结果重新组织为列存。
/// Inserts results into a column.
virtual void insertResultInto(ConstAggregateDataPtr place, IColumn & to) const = 0;复制
首先看聚合节点Aggregator是如何调用insertResultInto函数的
data.forEachValue([&](const auto & key, auto & mapped)
{
method.insertKeyIntoColumns(key, key_columns, key_sizes);
for (size_t i = 0; i < params.aggregates_size; ++i)
aggregate_functions[i]->insertResultInto(
mapped + offsets_of_aggregate_states[i],
*final_aggregate_columns[i]);
});复制
Aggregetor同样是遍历hash表之中的结果,将key列先组织成列存,然后调用insertResultInto函数将聚合计算的结果也转换为列存。 这里我们找一个sum函数的实现,来看看insertResultInto函数接口是如何工作的:
void insertResultInto(ConstAggregateDataPtr place, IColumn & to) const override
{
auto & column = static_cast<ColVecResult &>(to);
column.getData().push_back(this->data(place).get());
}复制
其实很简单,就是调用AggregateDataPtr,也就是AggregateFunctionSumData的get()函数获取sum计算的结果,然后添加到列内存之中。
get函数接口的实现如下:
T get() const
{
return sum;
}复制
2.聚合函数的注册流程
有了上述的背景知识,我们接下来举个栗子。来看看一个聚合函数的实现细节,以及它是如何被使用的。
AggregateFunctionSum
这里选取了一个很简单的聚合算子Sum,我们来看看它实现的代码细节。 这里我们可以看到AggregateFunctionSum是个final类,无法被继承了。而它继承IAggregateFunctionHelp类与IAggregateFunctionDataHelper类。
IAggregateFunctionHelp类 通过CRTP让父类可以直接调用子类的add函数指针而避免了虚函数调用的开销。IAggregateFunctionHelper类则包含了Data的模板数据类型,也就是上文提及的AggregateFunctionSumData进行内存结构的create,destory等等。
这里我们就重点看,这个类override了getName方法,返回了对应的名字时sum。并且实现了我们上文提到核心方法。
template <typename T, typename TResult, typename Data>
class AggregateFunctionSum final : public IAggregateFunctionDataHelper<Data, AggregateFunctionSum<T, TResult, Data>>
{
public:
using ResultDataType = std::conditional_t<IsDecimalNumber<T>, DataTypeDecimal<TResult>, DataTypeNumber<TResult>>;
using ColVecType = std::conditional_t<IsDecimalNumber<T>, ColumnDecimal<T>, ColumnVector<T>>;
using ColVecResult = std::conditional_t<IsDecimalNumber<T>, ColumnDecimal<TResult>, ColumnVector<TResult>>;
String getName() const override { return "sum"; }
AggregateFunctionSum(const DataTypes & argument_types_)
: IAggregateFunctionDataHelper<Data, AggregateFunctionSum<T, TResult, Data>>(argument_types_, {})
, scale(0)
{}
AggregateFunctionSum(const IDataType & data_type, const DataTypes & argument_types_)
: IAggregateFunctionDataHelper<Data, AggregateFunctionSum<T, TResult, Data>>(argument_types_, {})
, scale(getDecimalScale(data_type))
{}
DataTypePtr getReturnType() const override
{
if constexpr (IsDecimalNumber<T>)
return std::make_shared<ResultDataType>(ResultDataType::maxPrecision(), scale);
else
return std::make_shared<ResultDataType>();
}
void add(AggregateDataPtr place, const IColumn ** columns, size_t row_num, Arena *) const override
{
const auto & column = static_cast<const ColVecType &>(*columns[0]);
this->data(place).add(column.getData()[row_num]);
}
void merge(AggregateDataPtr place, ConstAggregateDataPtr rhs, Arena *) const override
{
this->data(place).merge(this->data(rhs));
}
void serialize(ConstAggregateDataPtr place, WriteBuffer & buf) const override
{
this->data(place).write(buf);
}
void deserialize(AggregateDataPtr place, ReadBuffer & buf, Arena *) const override
{
this->data(place).read(buf);
}
void insertResultInto(ConstAggregateDataPtr place, IColumn & to) const override
{
auto & column = static_cast<ColVecResult &>(to);
column.getData().push_back(this->data(place).get());
}
private:
UInt32 scale;
};复制
之前我们讲到AggregateFunction的函数就是通过AggregateDataPtr指针来获取AggregateFunctionSumData的地址,来调用add实现聚合算子的。我们可以看到AggregateFunctionSumData实现了前文提到的add, merge, write,read四大方法,正好与接口IAggregateFunction一一对应上了。
template <typename T>
struct AggregateFunctionSumData
{
T sum{};
void add(T value)
{
sum += value;
}
void merge(const AggregateFunctionSumData & rhs)
{
sum += rhs.sum;
}
void write(WriteBuffer & buf) const
{
writeBinary(sum, buf);
}
void read(ReadBuffer & buf)
{
readBinary(sum, buf);
}
T get() const
{
return sum;
}
};复制
ClickHouse在Server启动时。main函数之中会调用registerAggregateFunction的初始化函数注册所有的聚合函数。 然后调用到下面的函数注册sum的聚合函数:
void registerAggregateFunctionSum(AggregateFunctionFactory & factory)
{
factory.registerFunction("sum", createAggregateFunctionSum<AggregateFunctionSumSimple>, AggregateFunctionFactory::CaseInsensitive);
}复制
也就是完成了这个sum聚合函数的注册,后续我们get出来就可以愉快的调用啦。(这部分有许多模板派生的复杂代码,建议与源码结合梳理才能事半功倍~~)
3.要点梳理
第二小节解析了一个聚合函数与接口意义对应的流程,这里重点梳理聚合函数实现的源码要点:
- 各个聚合函数核心的实现
add,merge与序列化,内存结构初始化,内存结构释放的接口。 - 各个函数的实现需要继承IAggregateFunctionDataHelper的接口,而它的父类是
IAggregateFunctionHelper与IAggregateFunction接口。 - ClickHouse的聚合函数保证了每次循环遍历一个Block只调用一个
IAggregateFunction的聚合函数,这样最大程度上确保了向量化执行的可能性,减少了数据偏移与依赖。
4. 小结
好了,到这里也就把ClickHouse聚合函数部分的代码梳理完了。 除了sum函数外,其他的函数的执行也是同样通过类似的方式依次来实现和处理的,源码阅读的步骤也可以参照笔者的分析流程来参考。 笔者是一个ClickHouse的初学者,对ClickHouse有兴趣的同学,欢迎多多指教,交流。
5. 参考资料
官方文档 ClickHouse源代码
ClickHouse源码笔记5:聚合函数的源码再梳理 - 腾讯云开发者社区-腾讯云