n皇后问题
题目:
按照国际象棋的规则,皇后可以攻击与之处在同一行 或同一列 或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例1
输入:n = 4
输出:[[".Q..",
"...Q",
"Q...",
"..Q."],
["..Q.",
"Q...",
"...Q",
".Q.."]]
示例2
输入:n = 1
输出:[["Q"]]
提示:
1 <= n <= 9
分析:
其实就是要抓住可以搜索的三个条件
-
同行不能有棋子
//其实就是遍历列 for(int col = 0; col < n; col++){ if(map[x][col] == 'Q'){ return false; } } -
同列不能有棋子
//其实就是遍历行 for(int row = 0; row < n; row++){ if(map[row][y] == 'Q'){ return false; } } -
同斜线不能有棋子
同斜线比较麻烦,因为有左斜线和右斜线
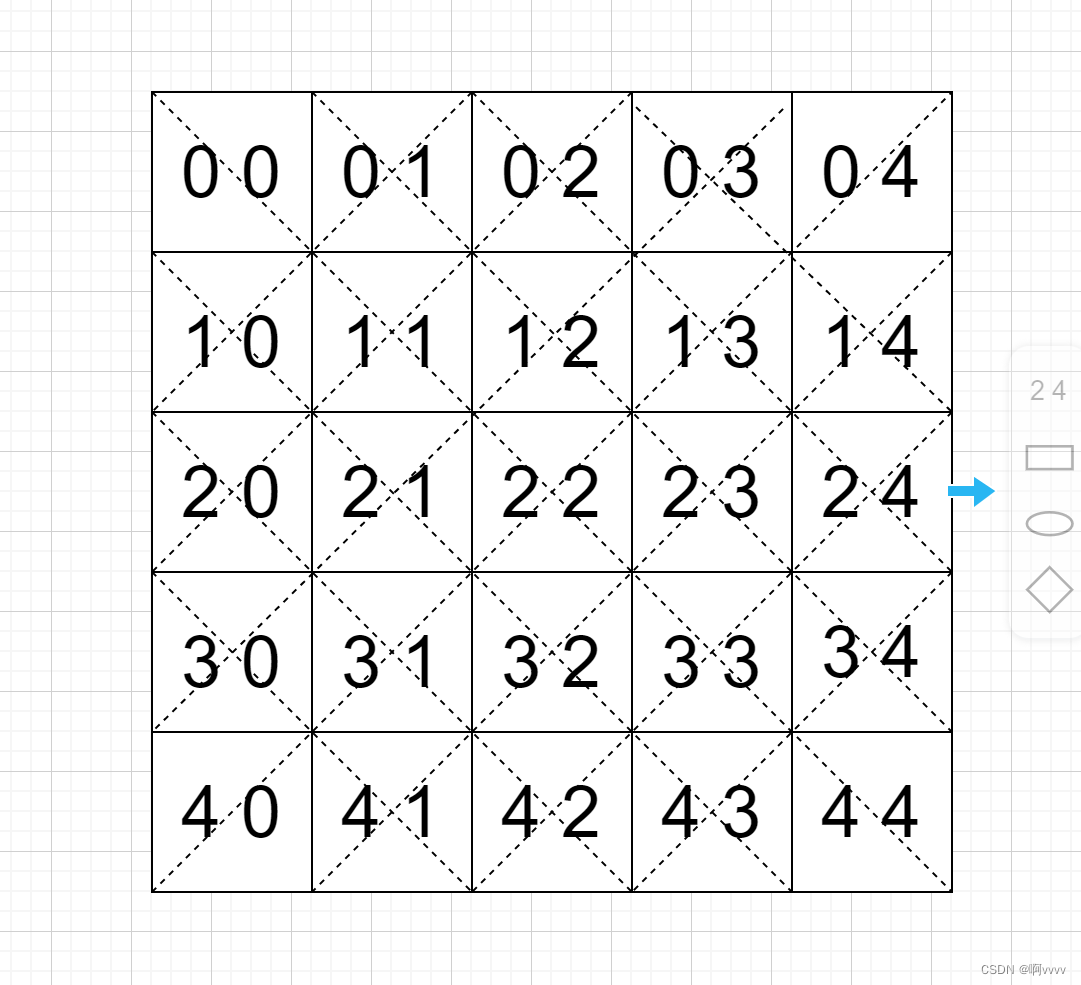
从当前点往右下
从当前坐标开始,往下x,y都增加
//往右下 int i = x + 1, j = y + 1; while(i < map.length && j < map.length){ if(map[i][j] == 'Q'){ return false; } i++; j++; }从当前点往左上
从当前坐标开始,往上x,y都减小
//往左上 i = x - 1; j = y - 1; while(i >= 0 && j >= 0 ){ if(map[i][j] == 'Q'){ return false; } i--; j--; } 从当前点往右上
从当前坐标开始,往上,x减小,y增加
//往右上 i = x - 1; j = y + 1; while (i >= 0 && j < map.length) { if(map[i][j] == 'Q'){ return false; } i--;j++; } 从当前点往左下
从当前坐标开始,往下,x增加,y减小
//往左下 i = x + 1; j = y - 1; while(i < map.length && j >= 0){ if(map[i][j] == 'Q'){ return false; } i++;j--; }
将上面三个代码合一
boolean isVaild(int x, int y,char[][] map){
//同一 行|列 不能有棋子
for(int i = 0; i < map.length; i++){
if(map[x][i] == 'Q' || map[i][y] == 'Q'){
return false;
}
}
//同一斜线不能有棋子
//往右下
int i = x + 1, j = y + 1;
while(i < map.length && j < map.length){
if(map[i][j] == 'Q'){
return false;
}
i++; j++;
}
//往左上
i = x - 1; j = y - 1;
while(i >= 0 && j >= 0 ){
if(map[i][j] == 'Q'){
return false;
}
i--; j--;
}
//往右上
i = x - 1; j = y + 1;
while (i >= 0 && j < map.length) {
if(map[i][j] == 'Q'){
return false;
}
i--;j++;
}
//往左下
i = x + 1; j = y - 1;
while(i < map.length && j >= 0){
if(map[i][j] == 'Q'){
return false;
}
i++;j--;
}
return true;
}
根据上面代码,我们也可以知道肯定需要当前点搜索的坐标
我们以行为递增条件,然后每次遍历一行
这样我们就有了坐标
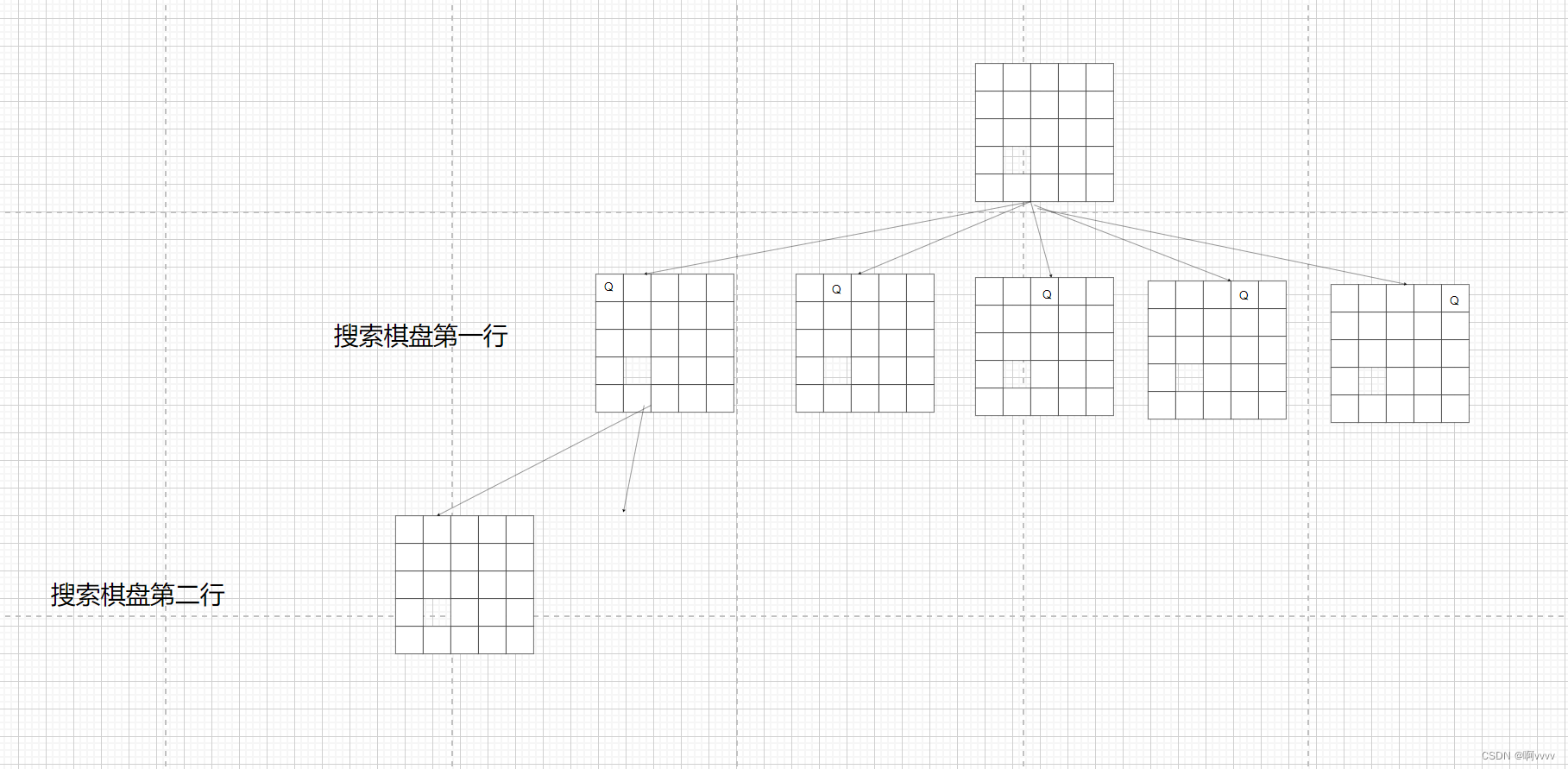
整体就是这样一个搜索过程,在最后一行收集答案即可
void dfs(int n, int row, char[][] map){
if(row == n){
//收集答案
List<String> tmp = new ArrayList();
for(int i = 0; i < n; i++){
tmp.add(new String(map[i]));
}
ans.add(tmp);
return;
}
for(int col = 0; col < n; col++){
if(isVaild(row,col,map) == true && map[row][col] == '.'){
//当前坐标可以放置棋子
map[row][col] = 'Q';
dfs(n,row+1,map);
//回溯,清除棋子
map[row][col] = '.';
}
}
}
整体代码如下
class Solution {
List<List<String>> ans = new ArrayList();
char[][] map;
public List<List<String>> solveNQueens(int n) {
map = new char[n][n];
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
map[i][j] = '.';
}
}
dfs(n,0,map);
return ans;
}
void dfs(int n, int row, char[][] map){
if(row == n){
//收集答案
List<String> tmp = new ArrayList();
for(int i = 0; i < n; i++){
tmp.add(new String(map[i]));
}
ans.add(tmp);
return;
}
for(int col = 0; col < n; col++){
if(isVaild(row,col,map) == true && map[row][col] == '.'){
map[row][col] = 'Q';
dfs(n,row+1,map);
map[row][col] = '.';
}
}
}
boolean isVaild(int x, int y,char[][] map){
//同一 行|列 不能有棋子
for(int i = 0; i < map.length; i++){
if(map[x][i] == 'Q' || map[i][y] == 'Q'){
return false;
}
}
//同一斜线不能有棋子
//往右下
int i = x + 1, j = y + 1;
while(i < map.length && j < map.length){
if(map[i][j] == 'Q'){
return false;
}
i++; j++;
}
//往左上
i = x - 1; j = y - 1;
while(i >= 0 && j >= 0 ){
if(map[i][j] == 'Q'){
return false;
}
i--; j--;
}
//往右上
i = x - 1; j = y + 1;
while (i >= 0 && j < map.length) {
if(map[i][j] == 'Q'){
return false;
}
i--;j++;
}
//往左下
i = x + 1; j = y - 1;
while(i < map.length && j >= 0){
if(map[i][j] == 'Q'){
return false;
}
i++;j--;
}
return true;
}
}