题目描述

原题描述：491. 递增子序列

解题思路

此题也是子集问题，但和 90.子集II （子集问题+startIndex去重） 的区别在于：（1）存储结果集判定条件；（2）输入数据的排列顺序；（3）去重方式

1. 存储结果集判定条件：只有当结果的个数大于或等于2时，才能存储；
2. 输入数据的排列方式：因存储的是原数据的递增子序列，因此需要保留原排列顺序
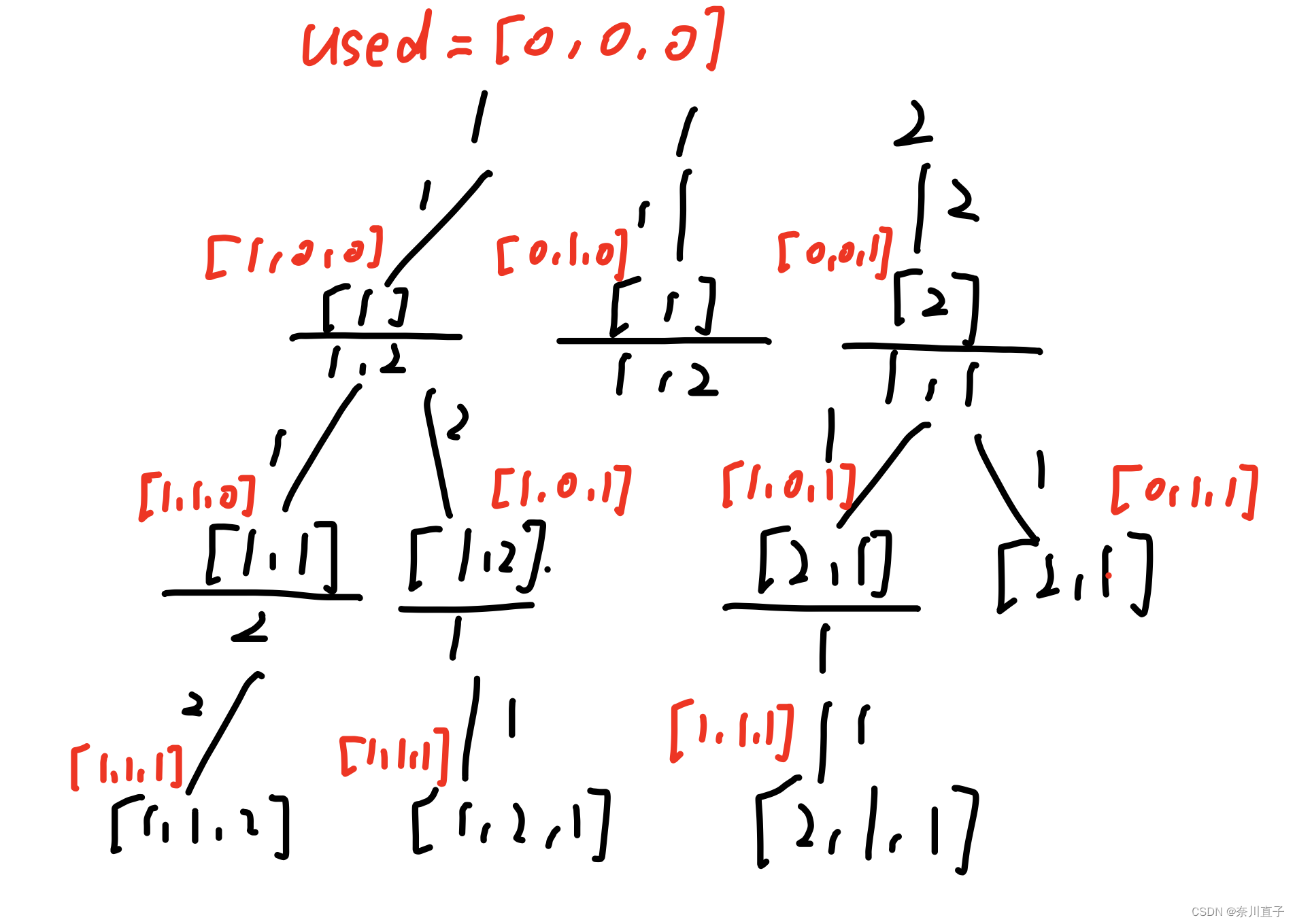
3. 去重方式：原数据中并不一定全是递增排序，因此可能会出现重复的数字，但并不相邻排列，因此不能用之前的去重方式进行去重。由于去重的为单层，出现过的重复元素，因此可以在每层遍历的时候设置一个Hash表判定对应元素是否出现过，若出现过，则跳过该种情况，没出现过则记录该种情况。

1、使用unordered_set作为Hash表

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(vector<int> nums, int startIndex) {
        // 将数列存入结果集中
        if(path.size() >= 2) {
            res.push_back(path);
        }        
        unordered_set<int> record;          // 树层去重，因此只用记录每层中是否选取重复数值
        for(int i = startIndex; i < nums.size(); i++) {
            // 结果中为空或者为递增数列时，如果每存储过该元素，则存入，否则跳过此种情况
            if(path.size() == 0 || nums[i] >= path.back()) {                
                if(record.find(nums[i]) == record.end()) {      // 没存过时存入，存过的话说明出现重复元素，跳过
                    record.insert(nums[i]);
                    path.push_back(nums[i]);
                    backtracking(nums, i + 1);
                    path.pop_back();
                }                
            }            
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {        
        backtracking(nums, 0);
        return res;
    }
}; 

2、使用数组作为Hash表

因为题中条件已经规定了nums的取值范围为[-100, 100]，故通过加上100的方式，把数映射到[0, 200]中，共201个数值。

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(vector<int> nums, int startIndex) {
        // 将数列存入结果集中
        if(path.size() >= 2) {
            res.push_back(path);
        }        
        int record[201] = {0};          // 采用数组方式，因nums范围为[-100,100]，使用+100作为偏移量，将nums映射到[0,200]之间（共201个数）
        for(int i = startIndex; i < nums.size(); i++) {
            // 结果中为空或者为递增数列时，如果每存储过该元素，则存入，否则跳过此种情况
            if(path.size() == 0 || nums[i] >= path.back()) {                
                if(record[nums[i] + 100] == 0) {      // 没存过时存入，存过的话说明出现重复元素，跳过
                    record[nums[i] + 100]++;
                    path.push_back(nums[i]);
                    backtracking(nums, i + 1);
                    path.pop_back();
                }                
            }            
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {        
        backtracking(nums, 0);
        return res;
    }
}; 

参考文章：491.递增子序列