491.递增子序列

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

示例 1：

输入：nums = [4,6,7,7]

输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]] 

示例 2：

输入：nums = [4,4,3,2,1]

输出：[[4,4]] 

问题分析：

注意本题不能先排序！！例如nums=[4,7,6,7]，如果排序成4,6,7,7就会出现[4,6,7,7]的集合，不符合要求，打破了原来数组的顺序。

 1、递归函数的参数与返回值

数组nums、搜索下标startIndex

2、终止条件

当path元素个数大于1就收集结果

3、单层搜索的逻辑

定义一个map，记录树层数字出现的次数，为了去重

依旧一个for循环

①如果单层遍历到第二个数字之后（path里已经有数字了）如果比当前path中最后一个数字小，就不是递增子序列，就继续向树层后遍历

②如果树层出现过遍历到的数字，就继续向树层后遍历（用getOrDefault方法）

然后就是用map记录、向path增加数字、回溯、移除等常规操作

class Solution {
        List<List<Integer>> result=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        backtracking(nums,0);
        return result;
    }
    public void backtracking(int[] nums,int startIndex){
        if (path.size()>1){//如果大于1就收集结果
            result.add(new ArrayList<>(path));
            //return; 不要加return，因为要取树上的所有节点
        }
        HashMap<Integer,Integer> map=new HashMap<>();//去重，记录树层数字出现次数
        for (int i=startIndex;i< nums.length;i++){
            if (!path.isEmpty()&&nums[i]<path.get(path.size()-1)){//要从进path的第二个元素开始，不加!path.isEmpty()报错
                continue;                                          // 如果此时遍历的数大于path里最后的数，则继续向后遍历
            }
            if(map.getOrDefault(nums[i],0)>=1){//如果树层出现过就继续遍历。getOrDefault如果存在key,则返回其对应的value,否则返回给定的默认值
                continue;
            }
            map.put(nums[i],map.getOrDefault(nums[i],0)+1);
            path.add(nums[i]);
            backtracking(nums,i+1);
            path.remove(path.size()-1);
        }

    }
}

---

 46.全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]

输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 

示例 2：

输入：nums = [0,1]

输出：[[0,1],[1,0]] 

示例 3：

输入：nums = [1]

输出：[[1]] 

问题分析：

本题不用startIndex，因为元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了

1、递归函数的参数与返回值

数组

2、终止条件

如果path的长度与数组长度相等就收集结果

3、单层搜索的逻辑

若path中已有这个元素，就跳过并继续遍历，之后就是常规操作。

class Solution {
    List<List<Integer>> result=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    public List<List<Integer>> permute(int[] nums) {
        backtracking(nums);
        return result;
    }
    public void backtracking(int[] nums){
        if (nums.length== path.size()){//全排序所有元素都加入到集合
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i=0;i<nums.length;i++){
            if (path.contains(nums[i])){//排除上一层已存在的数，寻找path中不存在的数
                continue;
            }
            path.add(nums[i]);
            backtracking(nums);
            path.remove(path.size()-1);
        }
    }
}

---

 47.全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]

输出： [[1,1,2], [1,2,1], [2,1,1]] 

示例 2：

输入：nums = [1,2,3]

输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

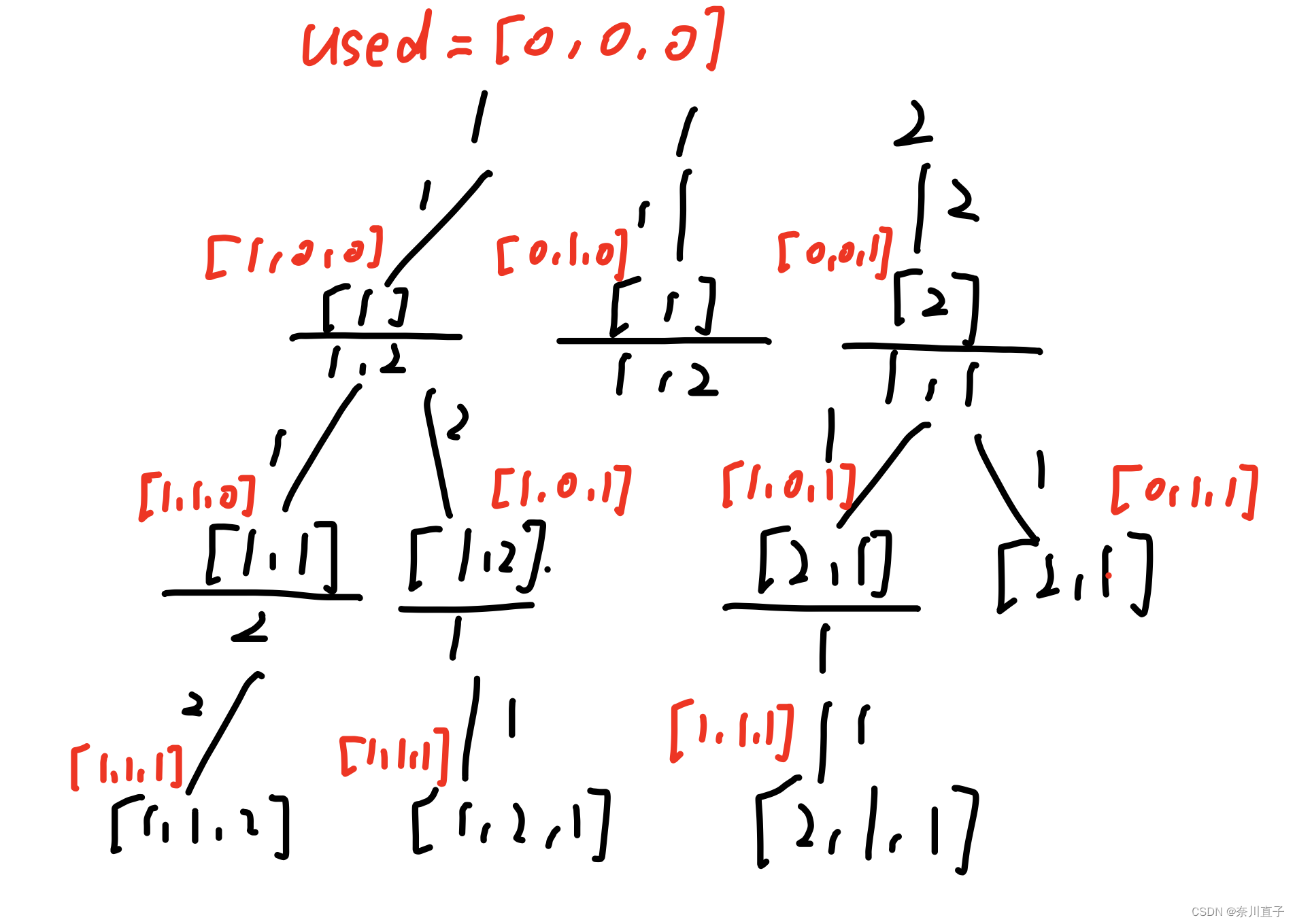
 问题分析：

1、递归函数的参数和返回值

int数组nums和boolean数组used

2、终止条件

当num和path的长度相等，就收集结果

3、单层搜索的逻辑

当i>0&&nums[i]==nums[i-1]&&used[i-1]==false时，继续遍历。used[i-1]==false代表前一个未读取（同一树层）

当used[i]==false就进行常规操作，意味着同一树枝还未开始处理

 

class Solution {
        List<List<Integer>> result=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
    public List<List<Integer>> permuteUnique(int[] nums) {
        boolean[] used=new boolean[nums.length];
        Arrays.fill(used,false);//布尔值分配给指定的布尔数组的每个元素。
        Arrays.sort(nums);
        backtracking(nums,used);
        return result;
    }
    public void backtracking(int[] nums,boolean[] used){
       if (nums.length== path.size()){
           result.add(new ArrayList<>(path));
           return;
       }
       for (int i=0;i< nums.length;i++){
           if (i>0&&nums[i]==nums[i-1]&&used[i-1]==false){//前一个未读取且相等（树层）
               continue;
           }
           if (used[i]==false){//同一树枝num[i]没开始处理
            used[i]=true;
           path.add(nums[i]);
           backtracking(nums,used);
           path.remove(path.size()-1);
           used[i]=false;
           }
       }
    }
}