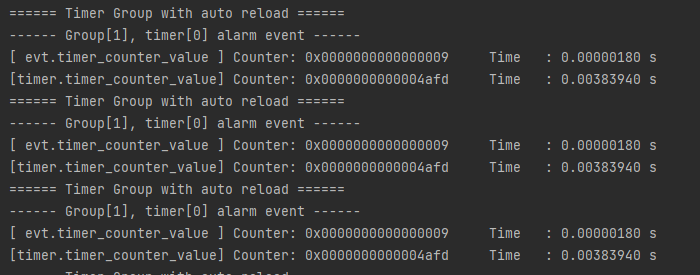
今天学了一下午这个
B
C
N
F
BCNF
BCNF与
3
N
F
3NF
3NF,有感而发,特来总结。好像好久不打键盘了,这手好像刚长出来的一样。本文浅显的分析一下两种范式的关系与不同以及判断方法和分解算法,以做总结。
B
C
N
F
BCNF
BCNF范式的定义如下:
设属性集合
U
=
{
A
,
B
,
C
,
D
,
.
.
.
,
}
U= \left\{ A,B,C,D,...,\right\}
U={A,B,C,D,...,},函数依赖集合
F
=
{
f
1
,
f
2
,
.
.
.
,
}
F=\left\{f_{1},f_{2},...,\right\}
F={f1,f2,...,},其中
f
1
f_{1}
f1形如
A
→
B
A\rightarrow B
A→B.如果模式
R
=
(
U
,
F
)
R=(U,F)
R=(U,F)满足
B
C
N
F
BCNF
BCNF范式,则应该有对于任意一个
f
i
=
H
1
→
H
2
f_{i}=H_{1}\rightarrow H_{2}
fi=H1→H2来说,
H
1
H_{1}
H1应该满足以下两个条件:
- H 1 H_{1} H1为超键
- 该依赖是平凡的( H 2 H_{2} H2是 H 1 H_{1} H1的子集)
这是为了防止有某个函数依赖
B
→
A
B \rightarrow A
B→A出现,其中
B
B
B不是超键,在此基础上我们来看
3
N
F
3NF
3NF的定义:
其与
B
C
N
F
BCNF
BCNF的差别为
3
N
F
3NF
3NF加入了第
3
3
3点
- 每一个在 H 2 − H 1 H_{2}-H{1} H2−H1中的属性都应该被某个候选键所包含
这里注意一个小细节,虽然第
3
3
3点是这样说,但是实际操作时对于一个函数依赖
α
→
β
\alpha \rightarrow \beta
α→β判断其是否是
3
N
F
3NF
3NF的,首先要看
α
\alpha
α是否是超键,如果不是超键就要看
β
\beta
β中的每个属性是否包含于
F
F
F的某个候选键当中。那么问题来了,问什么要加入这个奇怪的第
3
3
3条?其原因就是不让某个非主属性引起函数依赖的传递。
接下来说一下BCNF的分解方法:
对于一个不是
B
C
N
F
BCNF
BCNF的模式来说,遍历其所有的函数依赖,检查其是否满足上面那两条,如果不满足,就将当前模式分解为
R
1
=
(
α
,
β
)
R1=(\alpha,\beta)
R1=(α,β),
R
2
=
(
R
−
(
β
−
α
)
)
R2=(R-(\beta-\alpha))
R2=(R−(β−α))。分解完成之后,还要看
R
2
R2
R2是否是满足
B
C
N
F
BCNF
BCNF的:如果满足算法停止,否则继续对
R
2
R2
R2进行分解,在
R
2
R2
R2上检查
B
C
N
F
BCNF
BCNF时,一定要在
F
F
F的闭包
F
+
F^{+}
F+上看其是否是
B
C
N
F
BCNF
BCNF的。来看下面这个例子:
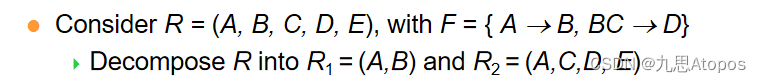
对于
R
2
R_{2}
R2来说,应该先看
R
2
R_{2}
R2上的函数依赖的左部有没有
R
2
R_{2}
R2上的候选键。但是
F
F
F中没有关于
R
2
R_{2}
R2的函数依赖,所以应该先求
F
F
F的闭包。在
F
F
F的闭包中有一个函数依赖为
A
C
→
D
AC \rightarrow D
AC→D,而
A
C
E
ACE
ACE为候选键,所以这一定不是
B
C
N
F
BCNF
BCNF,继续向下分解为
R
3
=
(
A
,
C
,
D
)
R3=(A,C,D)
R3=(A,C,D),
R
4
=
(
A
,
C
,
E
)
R4=(A,C,E)
R4=(A,C,E)
我们来回顾一下 B C N F BCNF BCNF的分解方法:
- 其分解的时候保证了无损连接
- 无损连接是啥?就是一个模式 R R R拆分成了 R 1 R_{1} R1和 R 2 R_{2} R2之后,经过 R 1 R_{1} R1与 R 2 R_{2} R2自然连接,又能转换回 R R R,前后 R R R中的行不多不少
- 为什么保留了无损连接?保留无损连接的条件是: R 1 ∩ R 2 → R 1 R_{1}\cap R_{2} \rightarrow R_{1} R1∩R2→R1 和 R 1 ∩ R 2 → R 2 R_{1}\cap R_{2} \rightarrow R_{2} R1∩R2→R2 这两个条件满足其一即可。对于 B C N F BCNF BCNF拆出的 R 1 R_{1} R1和 R 2 R_{2} R2其公共部分就是 α \alpha α,而 R 1 R_{1} R1( α , β ) \alpha,\beta) α,β)就已经满足了 R 1 ∩ R 2 → R 1 R_{1}\cap R_{2} \rightarrow R_{1} R1∩R2→R1 这个条件。
- 但是不能保证函数依赖都被留下。
- 为什么不能保证留下函数依赖?考虑这个例子: U = { A , B , C , D } U= \left\{ A,B,C,D\right\} U={A,B,C,D}, F = { A → C , B → C D } F=\left\{A\rightarrow C,B\rightarrow CD\right\} F={A→C,B→CD}, A A A不是候选键,分解为 ( A , C ) (A,C) (A,C)和 ( A , B , D ) (A,B,D) (A,B,D),则 B → C D B\rightarrow CD B→CD这个依赖一定保留不下来。
- 为什么一定要保留函数依赖?现在 R 1 R_{1} R1和 R 2 R_{2} R2是无损连接,假设有一个依赖 A → B A\rightarrow B A→B这个依赖没有被保留下来,现在向 R 1 ( 有 A 没 B ) R_{1}(有A没B) R1(有A没B)插入一行 A A A,向 R 2 ( 有 B 没 A ) R_{2}(有B没A) R2(有B没A)插入一行 B B B,在自然连接回去就会产生错误。
写到这里就不得不说一下
B
C
N
F
BCNF
BCNF与
3
N
F
3NF
3NF的关系了,首先来看一个例子:
设有一个属性集合
U
=
{
J
,
K
,
L
}
U= \left\{ J,K,L\right\}
U={J,K,L},其函数依赖集合为
F
=
{
J
K
→
L
,
L
→
K
}
F=\left\{JK\rightarrow L,L \rightarrow K\right\}
F={JK→L,L→K},先看候选键,其左部属性为
J
J
J,双部属性为
K
,
L
K,L
K,L,又发现
J
K
JK
JK和
J
L
JL
JL可以作为候选键,由于
L
→
K
L \rightarrow K
L→K不满足
B
C
N
F
BCNF
BCNF的定义,所以必须按照
B
C
N
F
BCNF
BCNF分解算法将其分解,但是我们注意到不论如何分解,
J
K
→
L
JK\rightarrow L
JK→L这个函数依赖一定不会被保留下来。所以
B
C
N
F
BCNF
BCNF虽然可以做到无损分解,但是不能保证能保留下函数依赖。所以放宽
B
C
N
F
BCNF
BCNF的条件,如果能满足第
3
3
3点,我们就将其称为好的
3
N
F
3NF
3NF。
下面说
3
N
F
3NF
3NF的分解算法:算出
F
F
F的正则覆盖
F
c
F_{c}
Fc,然后按照正则覆盖里的所有模式进行分解,如果最后没有原来
F
F
F的候选键,就加一个候选键组成的模式