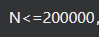目录
一. 基本概念
1.时间复杂度
2.空间复杂度
二.实例分析
实例(1):旋转数组
方法1:暴力旋转法(时间复杂度加空间复杂度分析)
方法2 :三步整体逆序法 (时间复杂度加空间复杂度分析)
实例(2):斐波那契递归的时间复杂度和空间复杂度分析
实例(3):169. 多数元素
方法1:随机法(时间复杂度加空间复杂度分析)
方法2:分治递归
方法3:投票算法(个人更喜欢称为擂台算法)
一. 基本概念
1.时间复杂度
(1)基本概念:
算法的时间复杂度的表达式是一个以问题规模N为自变量的函数。(问题规模一般与函数形参接收的值有关,可以是某个形参的值,字符串的长度,递归的阶数等等)
(2)计算方式
- 求算法的时间复杂度第一步:先求出问题规模为N情形下算法中基本语句的执行次数f(N).(基本语句可以是循环语句,分支语句等等)
- 对于递归函数我们还需计算出问题规模为N情形下,函数被调用的次数g(N);
- 求算法的时间复杂度第二步:将表达式f(N)*g(N)化为大O的渐进表示法(对于非递归函数g(N)为1)
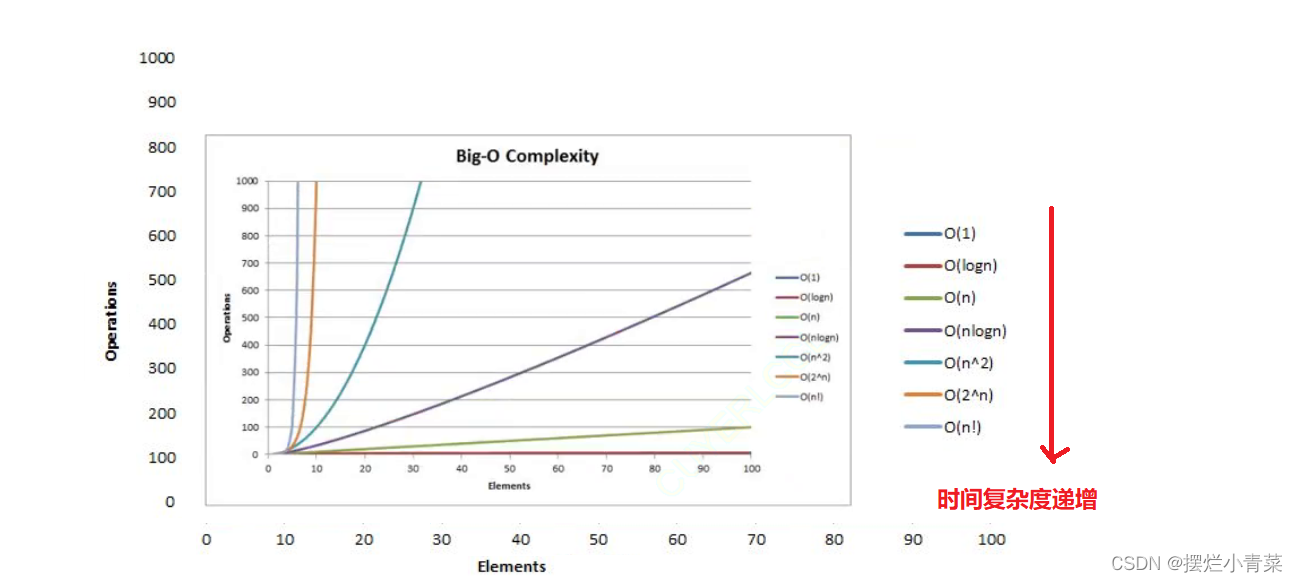
大O的渐进表示法:大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数,得到的结果就是大O阶。
另外有些算法的时间复杂度存在最好、平均和最坏情况
我们只关注算法的最坏运行情况。
2.空间复杂度
(1)基本概念:
- 空间复杂度也是以问题规模N为自变量的函数,是对一个算法在运行过程中临时占用存储空间大小的量度。
(2)计算方式
- 计算空间复杂度的第一步:
计算函数在执行时函数栈帧上同一时刻存在的变量的最大个数f(N),对于递归算法,还要需要计算递归过程中函数同一时刻开辟的函数栈帧的最大个数g(N)。
- 计算空间复杂度的第二步:
将g(N)*f(N)化为大O的渐进表示法(非递归函数g(N)=1);
表达式g(N)*f(N)化为大O的渐进表示法的规则与时间复杂度相应的规则完全一样。
二.实例分析
实例(1):旋转数组
189. 轮转数组 - 力扣(Leetcode)
- 问题描述:
给你一个数组,将数组中的元素向右轮转
k个位置,其中k是非负数。示例 :
输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]示例 :
输入:nums = [-1,-100,3,99], k = 2 输出:[3,99,-1,-100] 解释: 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100]
题解接口定义(C++):
class Solution { public: void rotate(vector<int>& nums, int k) { } };
方法1:暴力旋转法(时间复杂度加空间复杂度分析)
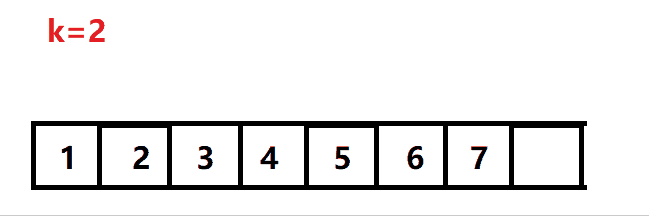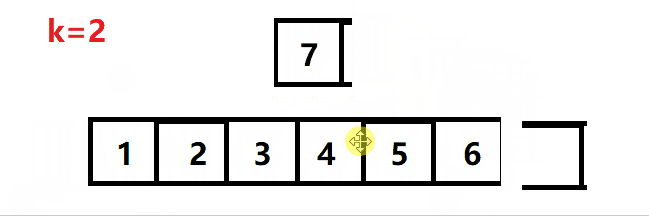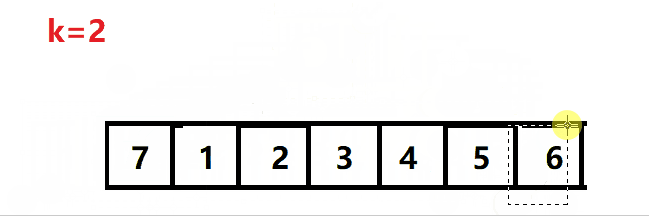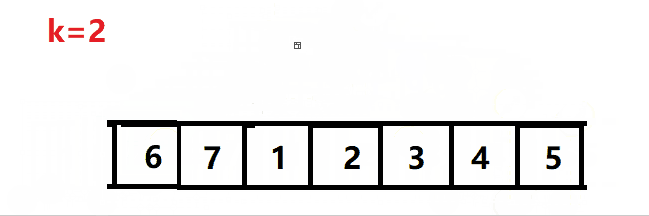
暴力旋转法的动图解析:
(暴力法无法通过leetcode的最后一个测试用例)
思路就是逐个字符地完成旋转:
class Solution { public: void rotate(vector<int>& nums, int k) { int sz = nums.size(); int n = k%sz; while(n--) { int i=sz-1; int tem = nums[sz-1]; for(i=sz-1;i>0;i--) { nums[i]=nums[i-1]; } nums[0]=tem; } } };
- 算法的时间复杂度分析:
由于每完成一个数字的旋转就要挪动N个数字,因此该算法for循环语句执行的次数为k*N
(k为要旋转的数字个数,N为数组的元素个数)(k取模后k<=N-1)
本例中k和N都是影响程序运行时间的变量:大O阶表达式中可以存在多个变量
算法的时间复杂度: O(N*k);
- 算法的空间复杂度分析:
算法中创建的临时变量个数为常数个;
算法的空间复杂度为: O(1)
暴力法无法通过leetcode的最后一个测试用例:
方法2 :三步整体逆序法 (时间复杂度加空间复杂度分析)
三步整体逆序法的思路:
class Solution { public: void Reverse (int start,int end,vector<int>& nums) { while(start < end) { int tem = nums[start]; nums[start]= nums[end]; nums[end]=tem; start++; end--; } } void rotate(vector<int>& nums, int k) { int sz = nums.size(); k%=sz; Reverse(0,sz-1,nums); Reverse(0,k-1,nums); Reverse(k,sz-1,nums); } };
- 算法的时间复杂度分析:(N为数组元素个数,k为要逆序元素个数)
- 第一步整体逆序,在逆序函数Reverse中循环语句总共要执行N/2次
- 第二步Reverse(0,k-1,nums),函数中循环语句总共执行k/2次
- 第三步Reverse(k,sz-1,nums),函数中循环语句总共执行(N-k)/2次
因此算法的时间复杂度为O(N);
- 算法空间复杂度分析:(N为数组元素个数,k为要逆序元素个数)
roate函数中创建的变量个数为常数个,Reverse函数中创建的变量也为常数个
因此算法的空间复杂度为O(1);
- 可见这是一个非常高效的算法。
实例(2):斐波那契递归的时间复杂度和空间复杂度分析
int Fib(int n) { if (n > 2) { return Fib(n - 1) + Fib(n - 2); } return (2 == n)? 2 : 1; }
- 时间复杂度分析:
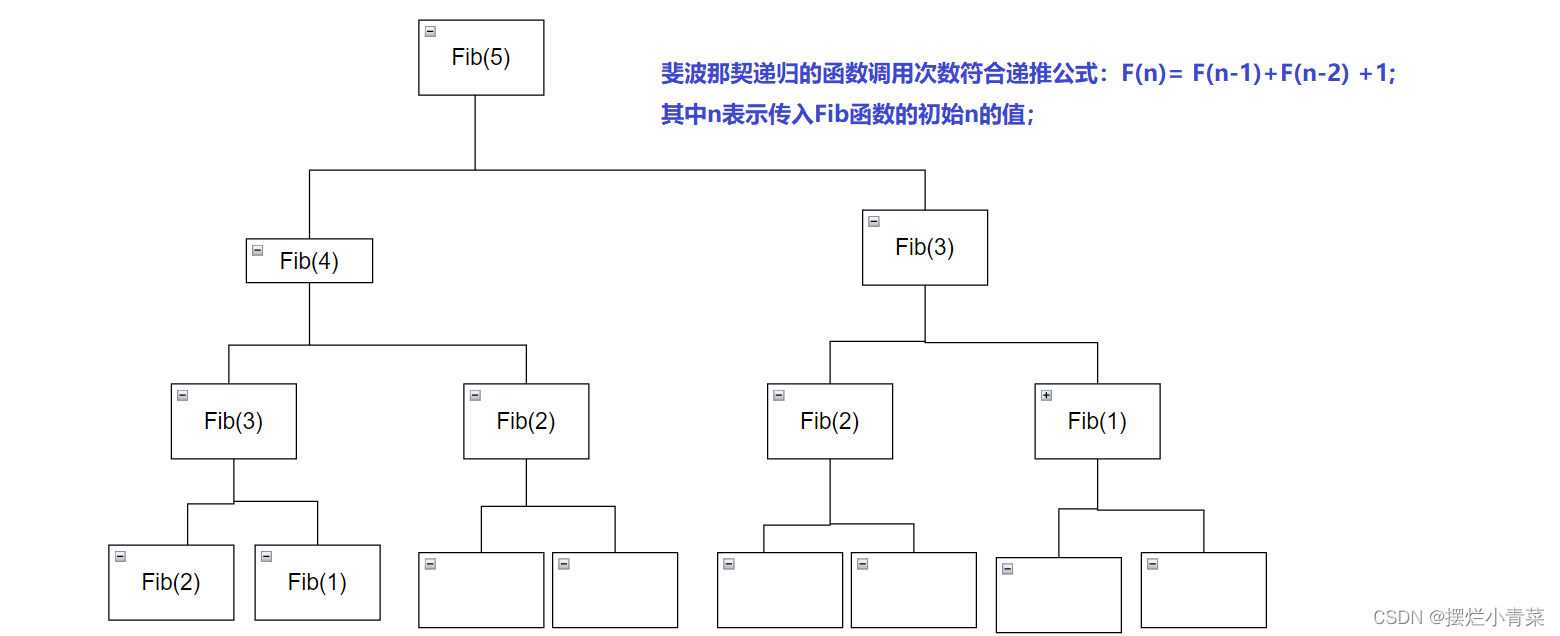
以n=5为例分析递归树:
然而求上述递推公式的通项式太过麻烦(要用到待定系数构造法),我们选择采用一种更简单的分析法:先将二叉树补全。
可以看到各层之间的函数调用次数成等比数列。
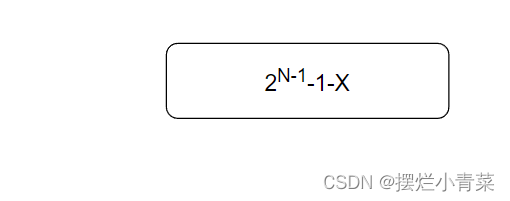
利用等比数列求和公式,可以求得Fib(N)的斐波那契递归函数调用总次数为:
当N足够大时,补上节点个数X相比于指数项可以忽略不计,因此根据大O阶的渐进表示法:
斐波那契递归的时间复杂度为:O(2^N)
- 空间复杂度分析:
4号Fib(2)压栈后会立马出栈:
因此分析可知:图中的四块栈帧空间会被各次函数调用重复利用,因此斐波那契递归函数Fib(N)同一时刻开辟的最大函数栈帧的个数为N个;
斐波那契递归的空间复杂度为: O(N);
实例(3):169. 多数元素
169. 多数元素 - 力扣(Leetcode)
- 问题描述:
给定一个大小为 n 的数组
nums,返回其中的多数元素。多数元素是指在数组中出现次数大于n/2的元素。你可以假设数组是非空的,并且给定的数组总是存在多数元素。示例 1:
输入:nums = [3,2,3] 输出:3示例 2:
输入:nums = [2,2,1,1,1,2,2] 输出:2
题解接口定义(C++):
class Solution { public: int majorityElement(vector<int>& nums) { } };
方法1:随机法(时间复杂度加空间复杂度分析)
由于我们要找的数组元素在数组中的存在个数占比超过百分之五十,因此我们可以考虑利用随机数生成器产生数组下标范围内的随机数来随机定位一个数组元素判断其是否符合题目条件。
class Solution { public: int majorityElement(vector<int>& nums) { srand((unsigned int)time(nullptr)); 用时间戳设定随机数种子 int sz = nums.size(); while(1) { int ans = (rand()%sz); 产生数组下标范围的随机整数 int i=0; int count =0; for(i=0;i<sz;i++) 判断随机定位的元素是否符合题目条件 { if(nums[i]==nums[ans]) { count++; } } if(count>sz/2) { return nums[ans]; } } } };该解法的时间复杂度分析十分有意思。
- 算法时间复杂度分析:
- 我们假设找到符合条件的数组元素总共要随机寻找X次
- 要求算法的时间复杂度,我们则要设法求出X的数学期望
- X是一个取值为整数1到正无穷的离散型随机变量
- 计算每个X的取值对应的概率,并得到X的分布列(为了方便计算分析我们假设多数元素恰好占数组元素个数的一半):
该分布列的数学期望为:
通过数列的错位相减法可以求出数列 i * (1/2)^i 的前X项和,再取X趋向正无穷的极限可以得到E(X)=2;
所以总体来说,大概只需随机取两次数组元素就可以取到多数元素,再经过两次遍历数组元素验证结果的正确性,该算法for语句执行次数的数学期望为2N(N为数组的元素个数)
因此算法的时间复杂度为:O(N)
- 算法的空间复杂度:
函数中创建的变量个数为常数个.
算法的空间复杂度为:O(1)
方法2:分治递归
如果数
a是数组nums的众数,如果我们将数组nums进行二等分,那么a必定是至少一部分的众数,因此我们就可以使用分治法解决这个问题:将数组二等分成左右两部分,分别求出左半部分的众数 a1 以及右半部分的众数 a2,随后在 a1 和 a2 中选出正确的众数。数组的左半边和右半边的众数又可以用相同的方法去求,由此便形成递归直到所有的子问题都是长度为
1的数组。
class Solution { public: int GetMulti(int left,int right , vector<int>&nums) //封装一个递归函数 { //递归函数的返回值代表是区间的众数 int mid = (left+right)/2; //找出二分点 int rightMulti=nums[left]; int leftMulti=nums[right-1]; if(right > left+1) //如果区间中的元素超过一个则继续二 //分区间 { rightMulti = GetMulti(mid,right,nums); //求右半区间的众数 leftMulti = GetMulti(left,mid,nums); //求左半区间的众数 } if(rightMulti==leftMulti)//左右半区间众数相同直接返回 { return rightMulti; } int i=0; int count =0; for(i=left;i<right;i++) //验证右半区间的众数是否为整个区间的众数(拿左边的判断也可以) { if(rightMulti==nums[i]) { count++; } } if(count>(right-left)/2) //判断若是众数则将其返回 { return rightMulti; } else { return leftMulti; } } int majorityElement(vector<int>& nums) { int sz = nums.size(); return GetMulti(0,sz, nums); } };
图解递归树:
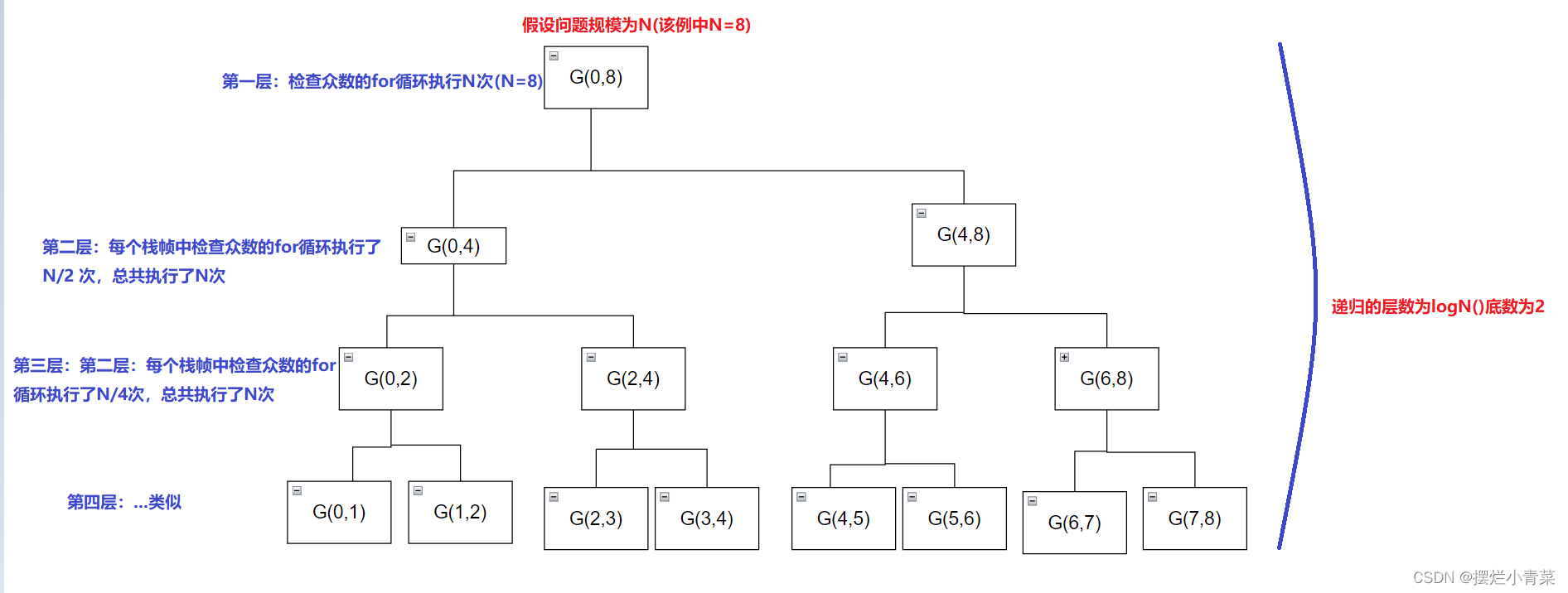
为了方便作图,我们将递归函数名简化为G,由于引用形参一直为nums不变,所以图中省去递归函数的引用形参:以八个元素的数组为例,递归函数的初始传参为G(0,8)
- 分治法在本题中合理性的分析:
- 算法时间复杂度分析:
可以看到递归树的每一层中,各函数检查众数的for循环执行的次数总和都为N,而递归的深度(递归树的层数为logN(二分对数底数为2))。
因此算法的时间复杂度为 : O(N*logN);
- 算法的空间复杂度分析:
从上面的递归树易知:该递归函数执行的过程中,同一时刻同时开辟的函数栈帧的最大个数为logN(底数为2),每个栈帧中的变量个数为常数个。
因此算法的空间空间复杂度为: O(logN)
方法3:投票算法(个人更喜欢称为擂台算法)
算法的核心思路:
如果我们把众数记为+1,把其他数记为−1,将它们全部加起来,显然和大于
0。
- 设定一个计数器count=0,创建一个变量用于存储假设的众数winner
- 第一个元素先赋值给假设的众数winner,count置为1,然后开始遍历数组。
- 遍历过程中,遇到和winner相等的元素,count++,否则count--
- 若count减为0,winner则替换为当前遍历到的数组元素,并且count置为1(表示当前元素为假设的众数)
- 根据算法的核心思路,winner最后存储的就是数组的众数
class Solution { public: int majorityElement(vector<int>& nums) { int sz = nums.size(); int winner =nums[0]; //先假定第一个元素为众数 int count =1; //count 置为1 int i=0; for(i=1;i<sz;i++) { if(nums[i]==winner) { count++; } else { count --; } if(0==count) //count减为0后winner则替换 { winner = nums[i]; count=1; } } return winner; } };
算法动画解析:
- 算法的时间复杂度:O(n);
- 算法的空间复杂度: O(1) ;