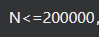排序(sorting)是按关键字的非递减或非递增顺序对一组记录重新进行整队(或排列)的操作。确切描述如下:

假设含有 n 个记录的序列为
{r1 ,r2 , … ,rn} (3-1)

它们的关键字相应为
{k1 ,k2 , … ,kn}

对式(3-1)的记录序列进行排序就是要确定序号 1,2,···,n 的一种排列
p1,p2 , … ,pn

使其相应的关键字满足如下的非递减(或非递增)的关系:
kp1<=kp2<=… <=kpn (3-2)

也就是使式(3-1)的记录序列重新排列成一个按关键字有序的序列
{rp1<=rp2<=…<=rpn} (3-3)

当待排序记录中的关键字 ki(i=1,2,…,n)都不相同时,则任何一个记录的无序序列经排序后得到的结果是唯一的;反之,若待排序的序列中存在两个或两个以上关键字相等的记录时,则排序所得到的记录序列的结果不唯一。假设 ki=kj(1<=i<=n,1<=j<=n, i 不等于 j),且在排序前的序列中 ri 领先于 rj (即i<j)。若在排序后的序列中 ri 仍领先于 rj,则称所用的排序方法是稳定的;反之,若可能使排序后的序列中 rj 领先于 ri ,则称所用的排序方法是不稳定的。

根据在排序过程中涉及的存储器不同,可将排序方法分为两大类:(1) 内部排序:在排序进行的过程中不使用计算机外部存储器的排序过程。(2) 外部排序:在排序进行的过程中需要对外存进行访问的排序过程。本文仅讨论各种内部排序的方法。

待排序的记录序列可以用顺序表表示,也可以用链表表示。但是我现在讨论的排序算法一律以下列说明的顺序表为操作对象。

内部排序的过程是一个逐步扩大记录的有序序列长度的过程。通常在排序的过程中.参与排序的记录序列中可划分为两个区域:有序序列区和无序序列区,其中有序序列区中的记录已按关键字非递减有序排列。使有序序列区中记录的数目增加一个或几个的操作称为一趟排序。下面以选择排序(selection sort)为例剖析内部排序的过程。

在选择排序的过程中，待排记录序列的状态为

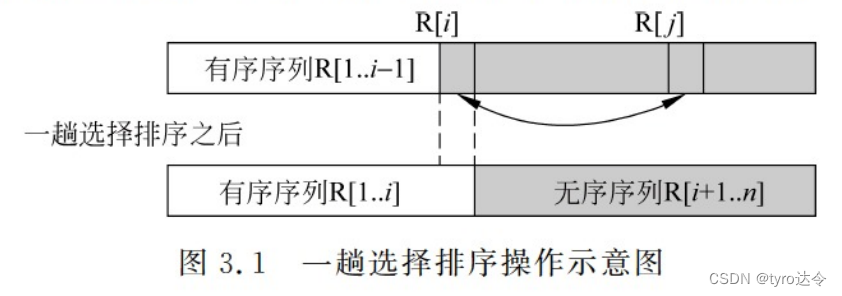
并且有序序列中所有记录的关键字均不大于无序序列中记录的关键字,则第 i 趟选择排序的操作是,从无序序列 R[i…n]的 n-i+1 个记录中选出关键字最小的记录 R[j]和 R[i]交换,从而使有序序列区从 R[1…i-1]扩大至 R[1…i],如图 3.1 所示。

一躺选择排序的算法如下：

整个选择排序的过程是一趟选择排序过程的多次重复,融合 SelectPass,其算法如下：

例如,对下列一组关键字:

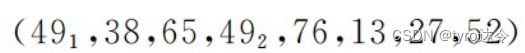
进行选择排序过程中,每一趟排序之后的状况如图 3.2 所示。其中 491和 492表示两个关键字同为 49 的不同记录.

从上述选择排序的过程可见,在内部排序的过程中主要进行下列两种基本操作:(1)比较两个关键字的大小；(2)将元素从一个位置移动至另一个位置。因此对内部排序的时间复杂度的分析就是以这两种操作的执行次数为依据。从算法 3.1 可见,在第趟选择排序过程中,需进行 n-i次关键字间的“比较”和交换记录时所需的至多 3 次“移动”记录操作。

整个选择排序过程中,需进行n(n-1)/2次关键字间的比较和至多 3(n-1)次移动记录因此它的时间复杂度为 O(n²)。选择排序是在原记录数据空间上通过记录的交换进行的。只在交换记录时需要用一个辅助工作变量,因此它的空间复杂度为 O(1)。

内部排序的方法很多,就排序算法的时间复杂度来区分,则可分为三类:(1)简单的排序方法,其时间复杂度为 O(n);(2)先进的排序方法,其时间复杂度为 O(nlogn);(3)基数排序,其时间复杂度为 O(dXn)。