08_旷视轻量化网络--ShuffleNet V1

1.1 简介

ShuffleNetV1是旷视科技（Face++）在2017年提出的一种专为移动设备设计的高效卷积神经网络（CNN）架构。它的主要目标是在保证模型精度的同时，极大地降低计算成本，使其更适合资源受限的环境，如手机和其他移动设备。

该网络出自论文《ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices》。

关键创新点

组卷积（Group Convolution）与通道重排（Channel Shuffle）：
- ShuffleNetV1利用组卷积来减少计算量。组卷积是将输入通道分为几个小组，每个小组独立进行卷积运算，这样可以显著减少计算资源的需求。但是，组卷积的一个缺点是它可能会限制信息在不同组之间的流动，导致特征表示能力下降。
- 为了解决这个问题，ShuffleNetV1引入了“通道重排”（Channel Shuffle）操作。在组卷积之后，这个操作会打乱组内特征图的顺序，促进不同组之间的信息交流，增强模型的学习能力并扩大感受野，从而改善了模型的性能。
优化1x1卷积：
- 注意到在ResNeXt等网络中，1x1卷积的计算量占据了相当大的比例，ShuffleNetV1进一步优化了这一部分，也将1x1卷积替换成组卷积，以进一步减少计算负担。

ShuffleNetV1 Block结构

每个基本块通常包含一个分组的1x1卷积（用于降维和升维），接着是一个分组的3x3卷积（用于特征提取），最后是通道混洗操作，以及可能的快捷连接（类似于ResNet中的残差连接）以保持梯度流动。

网络结构特点

ShuffleNetV1整体结构简洁高效，通过精心设计的组卷积和通道混洗操作，在不牺牲太多精度的前提下，实现了极高的计算效率，非常适合于实时的移动端应用。

应用场景

图像分类、物体检测、人脸识别等计算机视觉任务，特别是在对模型大小和运行速度有严格要求的移动或嵌入式设备上。

ShuffleNetV1的成功不仅在于其提出的创新技术，还在于它在实际应用中的高效表现，为后续轻量级网络的设计提供了重要的思路和方法。

1.2 分组卷积

ShuffleNetV1中的分组卷积（Group Convolution）是一种优化卷积层计算效率的技术，其灵感来源于AlexNet中使用的分组思想，但在这里被进一步发展和优化以适应轻量级网络的需求。

在传统的卷积操作中，所有的输入通道与输出通道之间都会进行卷积计算。而在分组卷积中，输入通道被划分为若干组，每一组内的输入通道仅与相应组的输出通道进行卷积。这样做可以显著减少计算量和参数数量，因为每个组的卷积操作是独立且并行的。

ShuffleNetV1中的应用

减少计算复杂度：通过将输入通道分成几个组，每个组内的卷积操作独立进行，减少了每次卷积的计算量。例如，如果输入通道被分为两组，那么原本需要在所有输入通道上执行的完整卷积现在只需在每组的一半通道上进行，这直接减少了计算资源的需求。
促进信息流动：尽管分组卷积有助于减少计算量，但它也可能导致不同组之间缺乏有效的信息交流。为了解决这个问题，ShuffleNetV1引入了**通道混洗（Channel Shuffle）**操作。在一组卷积操作之后，通道混洗会重新排列特征图的通道顺序，使得下一层的卷积可以跨越原先的组边界，促进特征信息的跨组传播，提高模型的表达能力。

优势

高效性：显著降低了模型的计算复杂度（FLOPs），使得模型在资源受限的设备上也能快速运行。
轻量化：减少了模型的参数数量，有助于减小模型体积，便于部署和传输。
性能保持：在减少计算成本的同时，通过通道混洗等创新设计保持了模型的识别精度。

（下图出自CondenseNet)

1.3 通道重排

ShuffleNetV1中的通道重排（Channel Shuffle）是一种设计技巧，旨在解决分组卷积（Group Convolution）后通道间信息流通受限的问题。在分组卷积中，输入通道被分成几个不相交的组，每组独立进行卷积操作，这样的处理虽然减少了计算量，但也限制了不同组间特征的交互，可能影响模型的表达能力。

通道重排的目的：

促进信息交流：通道重排的目的是打破分组卷积造成的组间信息隔离，通过随机或者系统性地重新排列通道顺序，使得下一阶段的卷积层能接收到混合来自不同组的特征信息，增强了特征的多样性与模型的泛化能力。
保持感受野：通过跨组的信息交流，帮助网络更好地捕捉全局上下文信息，避免了因分组而可能产生的局部过度专业化现象。

实现效果：

提升性能：通过增加特征图中信息的流动性，通道重排有助于提高模型的识别精度和泛化能力。
计算开销低：通道重排的操作相比额外的卷积层或复杂操作而言，计算成本几乎可以忽略不计，不会显著增加模型的运行时间或内存占用。

总结：

通道重排是ShuffleNetV1架构中的一项关键创新，它有效地解决了分组卷积的局限性，促进了特征通道间的跨组信息交流，是实现模型轻量化与高效性的核心技术之一。通过这种简单而有效的方法，ShuffleNetV1在保持高推理精度的同时，大幅降低了模型的计算复杂度和参数量，非常适合移动和嵌入式设备的应用场景。

通道重排的具体实现步骤：

输入准备：假设输入特征图的形状为(batch_size, channels, height, width)，其中channels是要被重排的通道数。
确定分组数：首先确定想要将通道分为多少组，记为G。这意味着每个组将包含大约channels // G个通道（如果channels不能被G整除，则前几个组可能多一个通道）。
通道拆分：将输入特征图的通道按组分开，形成一个形状为(batch_size, G, channels // G, height, width)的张量。这里，我们把原来的通道维度分割成了两个维度，一个是组的维度，另一个是组内通道的维度。
通道混洗：接下来是最关键的步骤，需要在组间对通道进行混洗。这可以通过以下方式完成：
- 将上述张量重塑为(batch_size, channels, height, width)的形式，但在这个过程中，需要对组内通道和组间的索引进行交错排列。具体来说，对于第g组内的第i个通道（在新排列中是第i + g*(channels // G)个通道），将其放置在新通道维度的第g + i*(G // channels)个位置上。这个过程可以用循环或者更高效的张量操作实现。
- 在PyTorch等框架中，这可以通过特定的张量操作函数（如torch.permute()和切片操作）或直接使用channel_shuffle函数实现，该函数通常会利用索引操作来进行高效混洗。
输出：经过上述操作后，得到的张量就是通道重排后的结果，维持了原有的(batch_size, channels, height, width)维度，但内部通道顺序已经按照指定的方式进行了重组。

通过这种通道重排机制，ShuffleNetV1能够确保分组卷积后的特征不仅在组内有较好的特征提取，同时组间信息也得到了有效的融合，从而提高了模型的表示能力。

1.4 网络结构

网络组成部分

基础块（Building Block）
- ShuffleNetV1的基础块由几个关键操作组成：分组1x1卷积用于降维，分组3x3卷积进行特征提取，以及通道重排操作。
- 具体来说，首先使用分组1x1卷积减少输入特征图的通道数，以降低计算成本，然后进行分组3x3卷积进行空间特征的提取。为了克服分组带来的信息孤立问题，紧随其后的通道重排操作混合了不同组的特征，确保信息在通道间充分交流。
- 如果需要保持输入和输出通道数一致，会在分组1x1卷积后加入一个升维的分组1x1卷积。
下采样块（Downsample Block）
- 在网络的某些阶段开始时，会使用带有步长为2的3x3卷积来缩小特征图的空间尺寸，同时增加通道数，实现下采样和特征的进一步提取。
网络层次结构
- ShuffleNetV1通常由多个阶段（stages）构成，每个阶段由多个基础块串联而成，每个阶段结束时可能会有下采样块来改变特征图的尺寸和深度。
- 网络的开始通常有一个标准卷积层用于图像到特征图的转换，接着是多个逐步增加深度的阶段，最后是全局平均池化（Global Average Pooling）、全连接层（Fully Connected Layer）和softmax分类器，用于图像分类任务。

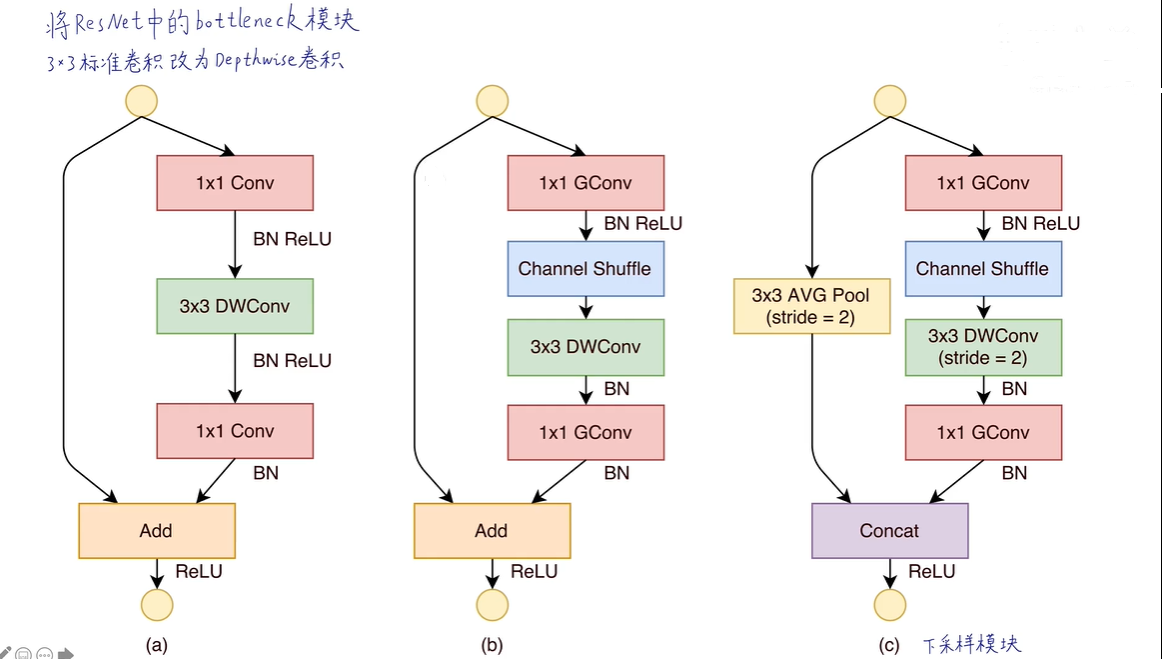
图（a）是一个典型的带有深度可分离卷积的残差结构，ShuffleNet_V1在此基础上设计出ShuffleNet单元。图（b）则是stride=1时的ShuffleNet单元，使用1x1分组卷积代替密集的1x1卷积，降低原1x1卷积的开销，同时加入Channel Shuffle实现跨通道信息交流。图（c）则是stride=2时的ShuffleNet单元，因为需要对特征图进行下采样，因此在图（b）结构基础上对残差连接分支采用stride=2的3x3全局平局池化，然后将主干输出特征和分支特征进行concat，而不再是add，大大的降低计算量与参数大小。

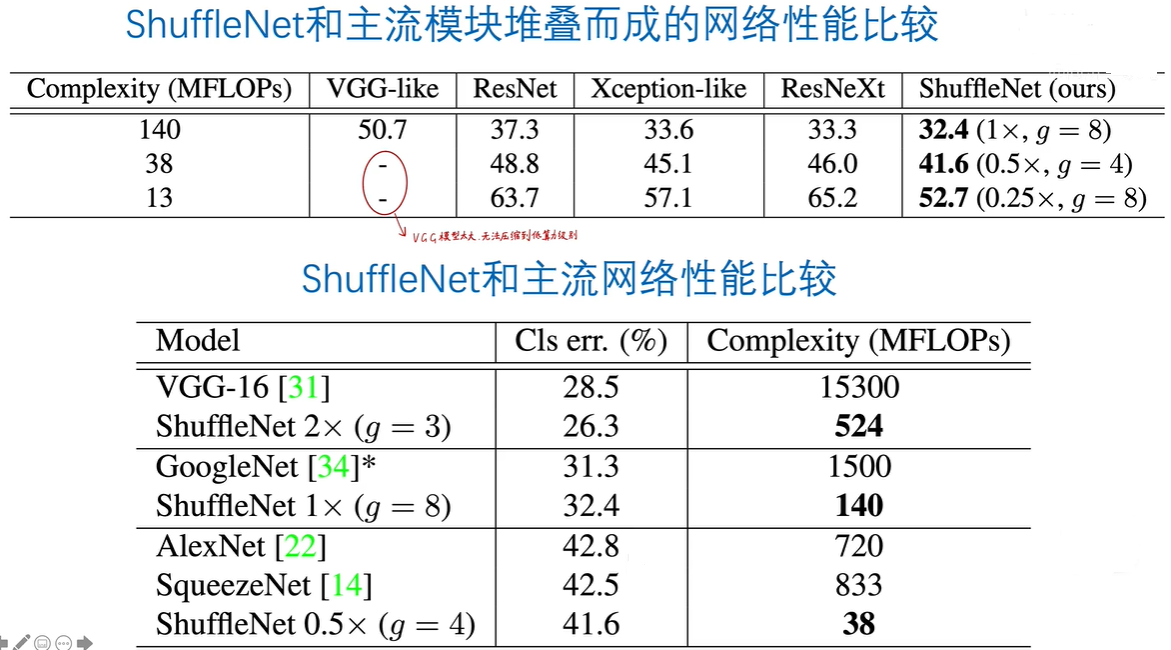
1.5 与其他网络的比较

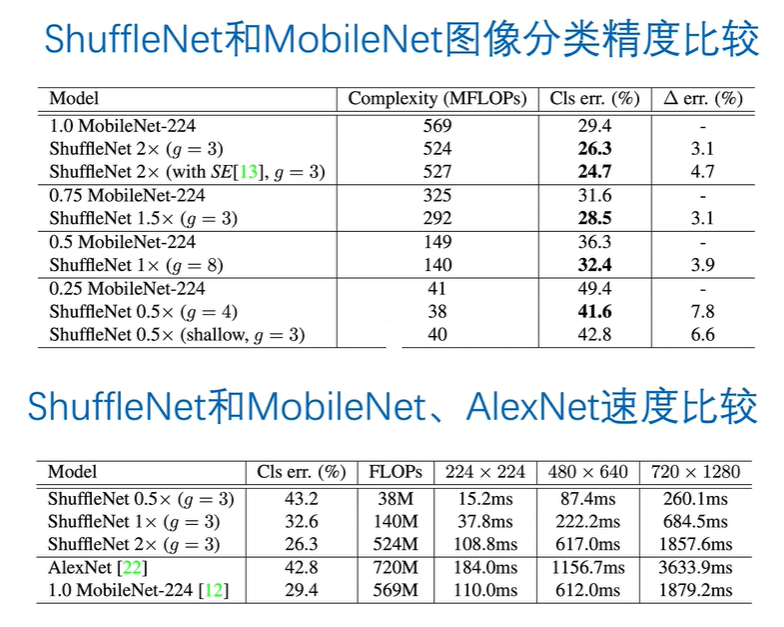
2.pytorch模型复现

# Author:SiZhen
# Create: 2024/6/4
# Description: pytorch实现shufflenetV1
import torch
import torch.nn as nn
import  torch.nn.functional as F
from  torch.nn import init
from collections import OrderedDict

# 1x1卷积（降维/升维）
def conv1x1(in_chans,out_chans,n_groups=1):
    return nn.Conv2d(in_chans,out_chans,kernel_size=1,stride=1,groups=n_groups)

#3x3深度卷积
def conv3x3(in_chans,out_chans,stride,n_groups=1):
    #不管步长为多少，填充总为1
    return nn.Conv2d(in_chans,out_chans,kernel_size=3,padding=1,stride=stride,groups=n_groups)

#通道混洗
def channel_shuffle(x,n_groups):
    #获得特征图所有维度的数据
    batch_size,chans,height,width=x.shape
    #对特征通道进行分组
    chans_group = chans//n_groups
    #reshape新增特征图的维度
    x = x.view(batch_size,n_groups,chans_group,height,width)
    #通道混洗（将输入张量的指定维度进行交换）
    x = torch.transpose(x,1,2).contiguous()
    #reshape降低特征图的维度
    x = x.view(batch_size,-1,height,width)
    return x

class ShuffleUnit(nn.Module):
    def __init__(self,in_chans,out_chans,stride,n_groups=1):
        super(ShuffleUnit, self).__init__()
        #1x1分组卷积降维后的维度
        self.bottle_chans = out_chans//4
        #分组卷积的分组数
        self.n_groups = n_groups
        #是否进行下采样
        if stride ==1:
            #不进行下采样，分支和主干特征形状完全一致，直接执行add相加
            self.end_op = 'Add'
            self.out_chans = out_chans
        elif stride==2:
            #进行下采样，分支和主干特征形状完全一致，分支也需进行下采样，而后再进行concat拼接
            self.end_op = 'Concat'
            self.out_chans = out_chans-in_chans

        #1x1 卷积进行降维
        self.unit_1 = nn.Sequential(conv1x1(in_chans,self.bottle_chans,n_groups=n_groups),
                                    nn.BatchNorm2d(self.bottle_chans),
                                    nn.ReLU())

        #3x3深度卷积进行特征提取
        self.unit_2 = nn.Sequential(conv3x3(self.bottle_chans,self.bottle_chans,stride,n_groups=n_groups),
                                    nn.BatchNorm2d(self.bottle_chans))

        #1x1 卷积进行升维
        self.unit_3 = nn.Sequential(conv1x1(self.bottle_chans,self.out_chans,n_groups=n_groups),
                                    nn.BatchNorm2d(self.out_chans))

        self.relu = nn.ReLU(inplace=True)

    def forward(self,inp):
        #分支的处理方式（是否需要下采样）
        if self.end_op == 'Add':
            residual = inp
        else:
            residual = F.avg_pool2d(inp,kernel_size=3,stride=2,padding=1)

        x = self.unit_1(inp)
        x = channel_shuffle(x,self.n_groups)
        x = self.unit_2(x)
        x = self.unit_3(x)
        #分支与主干融合的方式
        if self.end_op == 'Add':
            return self.relu(residual +x)
        else:
            return self.relu(torch.cat((residual,x),1))

class ShuffleNetV1(nn.Module):
    def __init__(self,n_groups,n_classes,stage_out_chans):
        super(ShuffleNetV1, self).__init__()
        #输入通道
        self.in_chans = 3
        #分组组数
        self.n_groups = n_groups
        #分类个数
        self.n_classes = n_classes

        self.conv1 = conv3x3(self.in_chans,24,2)
        self.maxpool = nn.MaxPool2d(3,2,1)

        #Stage 2
        op = OrderedDict()
        """
    op = OrderedDict() 这行代码创建了一个有序字典（Ordered Dictionary）对象。
    有序字典是Python中的一个数据结构，它类似于常规的字典，但保持了元素插入的顺序。
    这意味着当你遍历有序字典时，元素会按照你插入它们的顺序被访问，
    这对于某些需要保持操作或层顺序的应用场景非常有用，比如在定义神经网络模型时。
    在PyTorch的上下文中，OrderedDict 常常用于构建nn.Sequential模型时，来确保添加到模型中的层（模块）按照添加的顺序被应用。
         """
        unit_prefix = 'stage_2_unit_'
        #每个Stage的首个基础单元都需要进行下采样，其他单元不需要
        op[unit_prefix+'0'] = ShuffleUnit(24,stage_out_chans[0],2,self.n_groups)
        for i in range(3):
            op[unit_prefix+str(i+1)]=ShuffleUnit(stage_out_chans[0],stage_out_chans[0],1,self.n_groups)
        self.stage2 = nn.Sequential(op)

        #Stage 3
        op = OrderedDict()
        unit_prefix='stage_3_unit_'
        op[unit_prefix+'0'] = ShuffleUnit(stage_out_chans[0],stage_out_chans[1],2,self.n_groups)
        for i in range(7):
            op[unit_prefix+str(i+1)] = ShuffleUnit(stage_out_chans[1],stage_out_chans[1],1,self.n_groups)
        self.stage3 = nn.Sequential(op)

        #Stage 4
        op = OrderedDict()
        unit_prefix = 'stage_4_unit_'
        op[unit_prefix+'0'] = ShuffleUnit(stage_out_chans[1],stage_out_chans[2],2,self.n_groups)
        for i in range(3):
            op[unit_prefix+str(i+1)] = ShuffleUnit(stage_out_chans[2],stage_out_chans[2],1,self.n_groups)
        self.stage4 = nn.Sequential(op)

        #全局平均池化
        self.global_pool = nn.AdaptiveAvgPool2d((1,1))
        #全连接层
        self.fc = nn.Linear(stage_out_chans[-1],self.n_classes)
        #权重初始化
        self.init_params()

    #权重初始化
    def init_params(self):
        for m in self.modules():
            if isinstance(m,nn.Conv2d):
                nn.init.kaiming_normal_(m.weight,mode='fan_out')
                if m.bias is not None:
                    nn.init.zeros_(m.bias)
            elif isinstance(m,nn.BatchNorm2d):
                nn.init.ones_(m.weight)
                nn.init.zeros_(m.bias)
            elif isinstance(m,nn.Linear):
                nn.init.normal_(m.weight,0,0.01)
                nn.init.zeros_(m.bias)
    def forward(self,x):
        x = self.conv1(x)
        x = self.maxpool(x)
        x = self.stage2(x)
        x = self.stage3(x)
        x = self.stage4(x)
        x = self.global_pool(x)
        x = x.view(x.size(0),-1)
        x = self.fc(x)
        return x

#不同分组数对应的通道数也不同
stage_out_chans_list = [[144,288,576],[200,400,800],[240,480,960],
                        [272,544,1088],[384,768,1536]]

def shufflenet_v1_groups1(n_groups=1,n_classes=1000):
    model = ShuffleNetV1(n_groups=n_groups,n_classes=n_classes,
                         stage_out_chans=stage_out_chans_list[n_groups-1])
    return model

def shufflenet_v1_groups2(n_groups=2,n_classes=1000):
    model = ShuffleNetV1(n_groups=n_groups,n_classes=n_classes,
                         stage_out_chans=stage_out_chans_list[n_groups-1])
    return model

def shufflenet_v1_groups3(n_groups=3,n_classes=1000):
    model = ShuffleNetV1(n_groups=n_groups,n_classes=n_classes,
                         stage_out_chans=stage_out_chans_list[n_groups-1])
    return model

def shufflenet_v1_groups4(n_groups=4,n_classes=1000):
    model = ShuffleNetV1(n_groups=n_groups,n_classes=n_classes,
                         stage_out_chans= stage_out_chans_list[n_groups-1])
    return model

def shufflenet_v1_groupsother(n_groups=8,n_classes=1000):
    #groups>4
    modelother = ShuffleNetV1(n_groups=n_groups,n_classes=n_classes,
                         stage_out_chans=stage_out_chans_list[-1])
    return modelother
if __name__ == '__main__':
    device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
    model1 = shufflenet_v1_groups1().to(device)
    model2 = shufflenet_v1_groups2().to(device)
    model3 = shufflenet_v1_groups3().to(device)
    model4 = shufflenet_v1_groups4().to(device)
    modelother = shufflenet_v1_groupsother().to(device)