Tip: 如果你在进行深度学习、自动驾驶、模型推理、微调或AI绘画出图等任务，并且需要GPU资源，可以考虑使用UCloud云计算旗下的Compshare的GPU算力云平台。他们提供高性价比的4090 GPU，按时收费每卡2.6元，月卡只需要1.7元每小时，并附带200G的免费磁盘空间。通过链接注册并联系客服，可以获得20元代金券（相当于6-7H的免费GPU资源）。欢迎大家体验一下~

0. 简介

本文介绍了一种基于高斯喷洒的密集视觉同时定位与地图构建（VSLAM）新框架。最近基于高斯喷洒的SLAM取得了有希望的结果，但依赖于RGB-D输入且在跟踪方面较弱。为了解决这些局限性，《MGS-SLAM: Monocular Sparse Tracking and Gaussian Mapping with Depth Smooth Regularization》首次独特地将先进的稀疏视觉里程计与密集高斯喷洒场景表示相结合，从而消除了基于高斯喷洒的SLAM系统对深度图的依赖并增强了跟踪的鲁棒性。在这里，稀疏视觉里程计在RGB流中跟踪相机姿态，而高斯喷洒负责地图重建。这些组件通过多视图立体（MVS）深度估计网络相互连接。我们提出了一种深度平滑损失，以减少估计深度图的负面影响。此外，稀疏视觉里程计和密集高斯地图之间的尺度一致性通过稀疏-密集调整环（SDAR）得以保持。相关代码已经在Github开源了

1. 主要贡献

所提出系统的关键贡献总结如下：

• 首次引入结合稀疏视觉里程计和三维高斯喷洒的SLAM系统，实现仅使用RGB图像作为输入构建密集高斯地图。
• 开发了一种预训练的多视图立体（MVS）深度估计网络，该网络利用稀疏里程计关键帧及其姿态来估计先验深度图，从而为高斯地图重建提供关键的几何约束。
• 提出了一种几何深度平滑损失方法，以最小化估计的先验深度图不准确性对高斯地图的不利影响，并指导其对准到正确的几何位置。
• 提出了一种稀疏-密集调整环（SDAR）策略，以统一稀疏视觉里程计和密集高斯地图的尺度一致性。

2. 方法

我们的方法使用RGB图像作为输入，并行执行相机姿态估计和逼真的密集地图构建。正如图2所示，该方法的核心思想是使用预训练的多视图立体（MVS）网络将单目稀疏视觉里程计与密集高斯喷洒地图相结合，并通过稀疏-密集调整环（SDAR）保持稀疏点云地图与密集高斯地图之间的尺度一致性。

图2. 系统流程。系统以RGB视频流作为输入，并行运行前端和后端处理。在前端，稀疏视觉里程计从图像中提取特征块以估计姿态。这些估计的姿态和图像作为输入被传递到预训练的多视图立体（MVS）网络，该网络估计先验深度图。在后端，估计的先验深度图和图像结合前端提供的姿态被用作监督信息来构建高斯地图。前端和后端通过稀疏-密集调整环（SDAR）策略保持尺度一致性。

具体来说，在前端部分，通过跟踪RGB图像为后端提供粗略的相机姿态和先验深度图（参见III-A节）。在后端部分，使用高斯表示密集地图，并联合优化地图和前端提供的粗略姿态（参见III-B节）。在系统组件部分，报告系统初始化、系统关键帧选择以及通过SDAR策略校正稀疏点云地图与密集高斯地图之间的尺度（参见III-C节）。

3. 稀疏视觉里程计前端

为了实现更精确的相机姿态跟踪并在后端映射之前提供密集深度几何信息，我们的框架前端基于深度特征块视觉里程计（Deep Patch Visual Odometry, DPVO）算法【25】构建。DPVO是一种基于学习的稀疏单目视觉里程计方法，通过在特征块图上构建和优化误差来估计相机姿态并构建稀疏点云地图。

给定输入的RGB视频流，场景表示为一组相机姿态 $T\in SE(3{)}^N$ 和一系列从图像中提取的方形图像特征块 $P$，并将它们添加到双向特征块图中，该图将特征块与帧连接起来。方形特征块 $k$ 从帧$i$ 在帧 $j$ 中的重投影可以表示为：

$${\mathbf{p}}_j=\mathbf{K}{\mathbf{T}}_{ij}{\mathbf{p}}_i$$

其中，$\mathbf{K}$ 是相机内参矩阵，${\mathbf{T}}_{ij}$ 是从帧 $i$ 到帧 $j$ 的变换矩阵，${\mathbf{p}}_i$ 和 ${\mathbf{p}}_j$ 分别是特征块在帧 $i$ 和帧$j$ 中的坐标。

通过这种方式，DPVO 在特征块图上优化重投影误差，从而精确估计相机的姿态，并为后端的密集映射提供稀疏的几何深度信息。

$$\begin{array}{c}{\mathbf{P}}_k^{ij}\sim \mathbf{K}{\mathbf{T}}_j{\mathbf{T}}_i^{-1}{\mathbf{K}}^{-1}{\mathbf{P}}_k^i\end{array}$$

其中，$\mathbf{K}$ 是相机内参矩阵，${\mathbf{P}}_k^i=[u,v,1,d{]}^T$ 表示帧 $i$ 中的特征块 $k$，[u, v] 表示图像中的像素坐标，(d) 表示逆深度。

DPVO 的核心是一个更新算子，用于计算每条边 $(k,i,j)\in ϵ$ 的隐藏状态。它通过优化特征块图上的重投影误差来预测一个二维校正向量${\delta }_{ij}^k\in {\mathbb{R}}^2$ 和置信权重 ${\psi }_{ij}^k\in {\mathbb{R}}^2$。通过光流校正作为约束执行捆绑调整（Bundle Adjustment，BA），使用非线性最小二乘法进行迭代更新和相机姿态以及特征块深度的细化。捆绑调整的代价函数如下：

$$\begin{array}{c}\sum _{(k,i,j)\in ϵ}{\Vert \mathbf{K}{\mathbf{T}}_j{\mathbf{T}}_i^{-1}{\mathbf{K}}^{-1}{\mathbf{P}}_k^i-\left[{\bar{\mathbf{P}}}_k^{ij}+{\delta }_k^{ij}\right]\Vert }_{{\psi }_k^{ij}}^2\end{array}$$

其中，$\Vert \cdot {\Vert }_{\psi }$ 表示马氏距离，$\bar{\mathbf{P}}$ 表示特征块的中心。

3.1 多视图先验深度估计

后端的密集高斯映射需要几何深度图的监督。不同于之前的方法【26】，我们使用预训练的多视图立体（MVS）网络在DPVO的关键帧窗口上估计先验深度图，如图3所示。受单目深度估计方法【27】的启发，我们的MVS网络完全由二维卷积组成，采用由粗到细的结构逐步细化估计的先验深度图，以减少MVS网络的运行时间。

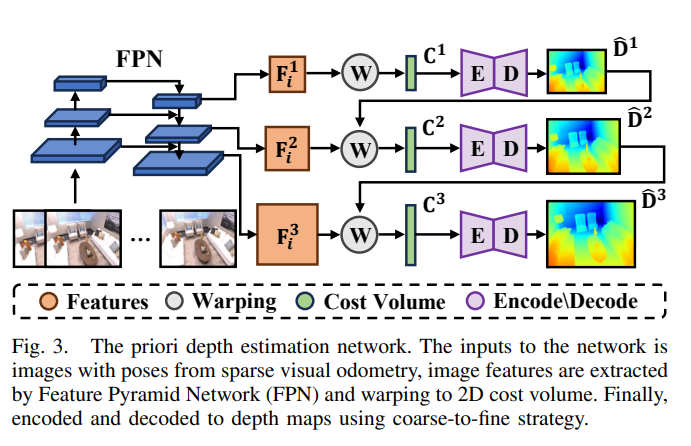
图3. 先验深度估计网络。网络的输入是来自稀疏视觉里程计的图像及其相机姿态。通过特征金字塔网络（Feature Pyramid Network, FPN）提取图像特征，并通过变形操作转换为二维代价体积。最后，采用由粗到细的策略对特征进行编码和解码，生成深度图。

具体来说，当前由稀疏视觉里程计跟踪的帧被用作参考图像 $I^0$。此外，我们使用之前的 $N$ 个关键帧作为一系列原始图像 $I^{n\in 1,\dots ,N}$。这些图像及其相应的相机姿态作为MVS网络的输入。利用特征金字塔网络（FPN）模块，我们为每个图像提取三层图像特征 $F_i^s$，其中 $s$ 表示层索引，$i$ 表示图像索引。每一层包含的图像特征是上一层长度和宽度的两倍。在每一层中，原始图像的图像特征通过可微分的变形操作与参考图像的图像特征点对点相乘，得到维度为 $D\times H^s\times W^s$ 的代价体积，并通过二维卷积编码和解码获得每一层的先验深度图。上一层估计的深度图被上采样作为下一层的参考深度图，以减少下一层的深度样本数量。每一层都进行类似的编码和解码操作，最终深度图在三层之后估计完成，以实现由粗到细的效果。我们的MVS深度估计网络在ScanNet数据集【28】上进行训练，采用尺度不变的损失函数以适应稀疏视觉里程计的相对姿态：

$$\begin{array}{c}{\mathcal{L}}_{si}^s=\sqrt{\frac{1}{H^s{W}^s}\sum _{i,j}{\left(g_{i,j}^s\right)}^2-\frac{\lambda }{{\left(H^s{W}^s\right)}^2}{\left(\sum _{i,j}{g}_{i,j}^s\right)}^2}\end{array}$$

其中，$g^s_{i,j} = \uparrow_{\text{gt}}(\log \hat{D}^s_{i,j} - \log D^{\text{gt}}{i,j}) $。$D^{\text{gt}}{i,j}$ 表示一个真实的深度图，通过上采样操作 ${\uparrow }_{\text{gt}}$ 对齐到预测深度 ${\hat{D}}_{i,j}^s$ 的大小。常数 $\lambda$ 为 0.85。

此外，损失函数中还添加了多视图损失和法线损失，以保持深度估计的几何一致性：

$$\begin{gathered} {\mathcal{L}}_{mv}^s=\frac{1}{N{H}^s{W}^s}\sum _{n,i,j}\left|{\uparrow }_{gt}\log {\mathbf{T}}_{0n}({\hat{D}}_{i,j}^s)-\log D_{n,i,j}^{gt}\right|\text{(4)} \\ {\mathcal{L}}_{normal}^s=\frac{1}{2H^s{W}^s}\sum _{i,j}(1-{\hat{N}}_{i,j}^s\cdot N_{i,j}^s)\text{(5)} \end{gathered}$$

其中，$T_{0n}$ 表示从参考图像到原始图像 $n$ 的变换矩阵。${\hat{N}}_{i,j}^s$ 和$N_{i,j}^s$ 分别表示预测的法向量和真实的法向量。最终的多视图立体（MVS）深度估计网络损失函数如下：

$$\mathcal{L}=\sum _{s=0}^l\frac{1}{2^s}({\lambda }_{si}{\mathcal{L}}_{si}^s+{\lambda }_{mv}{\mathcal{L}}_{mv}^s+{\lambda }_{normal}{\mathcal{L}}_{normal}^s)(6)$$

其中 $l$ 为2，我们将损失权重 ${\lambda }_{si}$、${\lambda }_{mv}$ 和 ${\lambda }_{normal}$ 分别设置为1.0、0.2和1.0。

4. 三维高斯喷洒映射后端(核心)

后端的主要职责是进一步优化前端提供的粗略姿态并映射高斯场景。这个部分的关键在于可微渲染和深度平滑正则化损失，通过计算渲染结果与真实值之间的损失，并通过反向梯度传播调整粗略姿态和高斯地图。

4.1 可微高斯地图表示

我们使用三维高斯喷洒作为场景的密集表示。三维高斯喷洒是一种高效的三维空间表示方法，它以类似点云的方式映射场景，避免了像NeRF那样在空间的空白区域进行采样，并且能够实时渲染。单个三维高斯 $p_i\in {\mathbb{R}}^3$ 在三维场景中的影响如下：

$$f(p_i)=\sigma (o_i)\cdot \exp (-\frac{1}{2}(p_i-{\mu }_i{)}^T{\Sigma }^{-1}(p_i-{\mu }_i))(7)$$

其中，$o_i\in \mathbb{R}$ 表示高斯分布的透明度，${\mu }_i\in {\mathbb{R}}^3$ 是高斯分布的中心，$\Sigma =RS{S}^T{T}^T\in {\mathbb{R}}^{3,3}$ 是协方差矩阵，由 $S\in {\mathbb{R}}^3$ 缩放分量和 $R\in {\mathbb{R}}^{3,3}$ 旋转分量计算得出。三维高斯分布投影到图像平面的表达式如下：

$$\begin{array}{rl}{\mu }_I& =\pi ({\mathbf{T}}_{CW}\cdot {\mu }_W)\\ {\Sigma }_I& =JW{\Sigma }_W{W}^T{J}^T\end{array}\text{\hspace{1em}(8)(9)}$$

其中，$\pi (\cdot )$ 表示三维高斯中心的投影，$T_{CW}\in SE(3)$ 是从世界坐标到相机坐标的三维空间变换矩阵，$J$ 是投影变换的雅可比矩阵的线性近似，$W$ 是 $T_{CW}$ 的旋转分量。方程 (8) 和 (9) 是可微分的，这确保了高斯地图可以使用一阶梯度下降来连续优化地图的几何和光度，使地图能够渲染为逼真的图像。一个像素颜色 $C_p$ 是通过喷洒和混合来自 $N$ 个高斯的结果：

$$\begin{array}{c}{C}_p=\sum _{i\in N}{c}_i{o}_i\prod _{j=1}^{i-1}(1-o_j)\end{array}\text{\hspace{1em}(10)}$$

其中，$c_i$ 是高斯 $i$ 的颜色，$o_i$ 是高斯 $i$ 的透明度。

4.2 映射优化损失

我们修改了原始三维高斯喷洒的损失函数，并添加了更多几何约束，使其更适合像 SLAM 这样的在线映射系统。具体来说，我们的损失函数由四个部分组成：光度损失、深度几何损失、深度平滑正则化损失和各向同性损失。

在光度损失中，计算当前相机姿态 $T_{CW}$ 下渲染的彩色图像与真实彩色图像之间的 L1 损失：

$$\begin{array}{c}{\mathcal{L}}_{pho}={\Vert I(\mathcal{G},{\mathbf{T}}_{CW})-I^{gt}\Vert }_1\end{array}\text{\hspace{1em}(11)}$$

其中，$I(\mathcal{G},T_{CW})$是从高斯分布 $\mathcal{G}$ 渲染的彩色图像，$I_{gt}$ 是真实的彩色图像。

$$\begin{array}{c}{D}_p=\sum _{i\in N}{z}_i{o}_i\prod _{j=1}^{i-1}(1-o_j)\end{array}\text{\hspace{1em}(12)}$$

为了提高高斯地图的几何精度，我们同样渲染了深度图，类似于方程 (10)：

$$\begin{array}{c}{\mathcal{L}}_{geo}={\Vert D(\mathcal{G},{\mathbf{T}}_{CW})-{\bar{D}}_d\Vert }_1\end{array}\text{\hspace{1em}(13)}$$

其中，$D(G,T_{CW})$ 是从高斯分布 $\mathcal{G}$ 渲染的深度图，${\overline{D}}_d$ 是通过 SDAR 策略优化的先验深度图。优化过程见第 III-C 节。

从 MVS 网络获得的先验深度图可能并不完全准确。如图 4 所示，直接使用这些深度图会在高斯地图的几何重建中导致错误的引导。因此，我们引入了深度平滑正则化损失：

$$\begin{array}{c}{\mathcal{L}}_{smooth}={\Vert d_{i,j-1}-d_{i,j}\Vert }_2+{\Vert d_{i+1,j}-d_{i,j}\Vert }_2\end{array}\text{\hspace{1em}(14)}$$

其中，$d_{i,j}$ 表示渲染深度图中像素坐标 $(i,j)$ 的深度值。通过对渲染深度图中相邻像素进行正则化，它减少了先验深度图误差的影响。

…详情请参照古月居