这是C++算法基础-基础算法专栏的第七篇文章，专栏详情请见此处。

引入

        在C++语言中，int的可存储数据范围是-2147483648~2147483647，long long的可存储数据范围是-9223372036854775808~9223372036854775807，但是如果一些数据比long long的可存储数据还要大时，我们就不得不使用别的方法去储存与计算了，这种方法就是高精度计算。

        下面我们就来讲高精度加法的实现。

定义

        高精度计算（Arbitrary-Precision Arithmetic），也被称作大整数（bignum）计算，运用了一些算法结构来支持更大整数间的运算（数字大小超过语言内建整型）。

前置过程

        这里我们用数组来实现高精度计算。

        清除

        先做一个简单的清除数组的操作。

void clear(int a[]){
	for(int i=0;i<L;i++)
		a[i]=0;
}

        输入与储存 

        高精度计算数字的规模太大了，需要输入一个字符串，再把它放进数组里。

Q：怎样字符串转化为数组呢？

A：字符串的每一位都是字符，若想把它转化为数组，就需要用ASCII码进行偏移操作，将此字符减去‘0’。

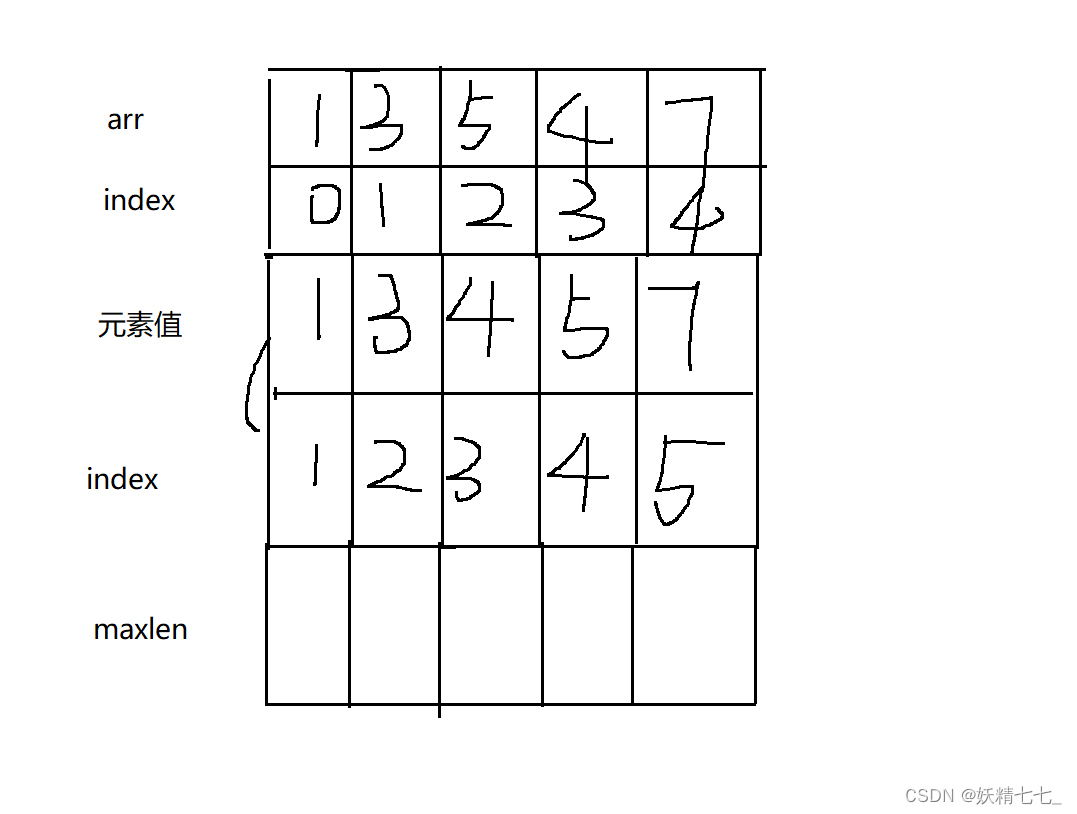
        还有一个问题，读入字符串时，数字最高位在字符串首（下标小的位置）。但是实际我们习惯在下标最小的位置存放数字的个位，即存储一个反转的字符串。

Q：为什么要存储一个反转的字符串呢？

A：这么做是因为两个数进行运算时通常从个位开始，且运算时数字的长度也有可能发生变化，但我们希望同样个位始终保持对齐，所以反转存储是最好的方式。

        下面给出高精度计算的读入与储存代码：

void read(int a[]){
	cin>>s;
	int L=s.size();
	for(int i=0;i<L;i++)
		a[i]=s[L-1-i]-'0';
}

        输出

        输出一个数组没什么难的，但在高精度计算中，我们不希望将数组中的前导零输出，故需要从最高位开始向下寻找第一个非零的位置，从这里开始输出。

        你会发现在代码中，终止条件是而不是，这是因为若这个数字本身就是0，则需要输出个位。

        下面给出高精度计算的输出代码：

void print(int a[]){
	int i;
	for(i=L-1;i>=1;i--){
		if(a[i]!=0)
			break;
	}
	for(;i>=0;i--)
		cout<<a[i];
	cout<<endl;
}

主体过程

        高精度加法的原理和小学学习的竖式加法是一样的。

​

        概括来说，从个位开始，将两个加数相对应的每一位相加，存进和的对应位置上，若当前位达到，进位，也就是将下一位加，并把当前位减。

        用高精度计算，先加个位，得，发现大于等于，所以将减，得，将其存入答案的个位，将十位加；

        再加十位，得，发现大于等于，所以将减，得，将其存入答案的十位，将十位加；

        最后加百位，得，发现不大于等于，所以直接将存入答案的百位。得到答案。

        下面给出高精度加法的代码：

void add(int a[],int b[],int c[]){
	clear(c);
	for(int i=0;i<L-1;++i){
		c[i]+=a[i]+b[i];
		if(c[i]>=10){
			c[i+1]+=1;
			c[i]-=10;
		}
	}
}

上一篇-浮点数二分查找的实现    C++算法基础专栏文章    下一篇-高精度减法的实现

每周六更新一篇文章，内容一般是自己总结的经验或是在其他网站上整理的优质内容

点个赞，关注一下呗~