前言

大家好久不见，今天想跟大家分享如何优雅地控制边界，边界的控制不是算法，更像是一门艺术，优秀的程序员能够优雅地控制边界，要成为一名优秀的程序员，我们就要去学习如何控制边界~

一、为什么需要控制边界？

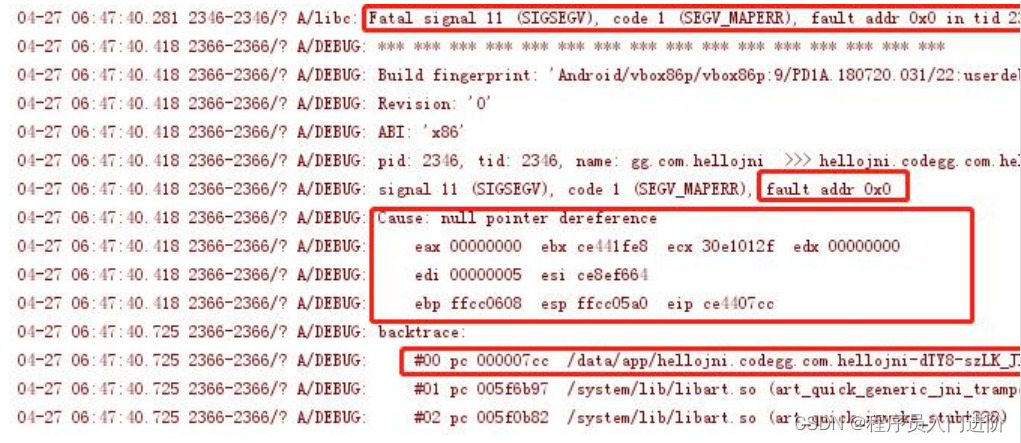
国有国界，家有家规，贸然地使用不属于自己的东西，是一件很危险的事情~，因此我们需要合理地控制边界！不然你很容易看到以下报错 ~

IndexOutOfBoundsException（JAVA）
Segmentation Fault（LINUX）

二、怎么优雅地控制边界？

回答这个问题前，我想问大家一个问题：让大家给一个班级分组，你会如何分？

方案一：按照固定人数来分
方案二：随意分，按照心情来分

为了方便以后的管理，我想你一定会选择方案一的~

那如何优雅地控制边界呢？

重要
统一管理方案，是优雅控制边界的重要方法！

三、令人抓狂的二分查找

3.1 题目概述

二分查找相信大家并不陌生，虽然原理很简单，但我们在手撕代码的时候就会出现各种各样的小问题，当你好不容易解决掉这些问题，却也一直在发懵，下次见到依然是发懵的状态，其实这就是边界没有搞清的原因。
再来读一下题：

点击做题：leetcode 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

3.2解题思路

二分查找的逻辑比较简单：在一个有序数组里，拿我们的目标值与target（目标值）与 mid 对应的值进行比较，根据比较的值，直接将区间缩小一半，直到找到那个数为止

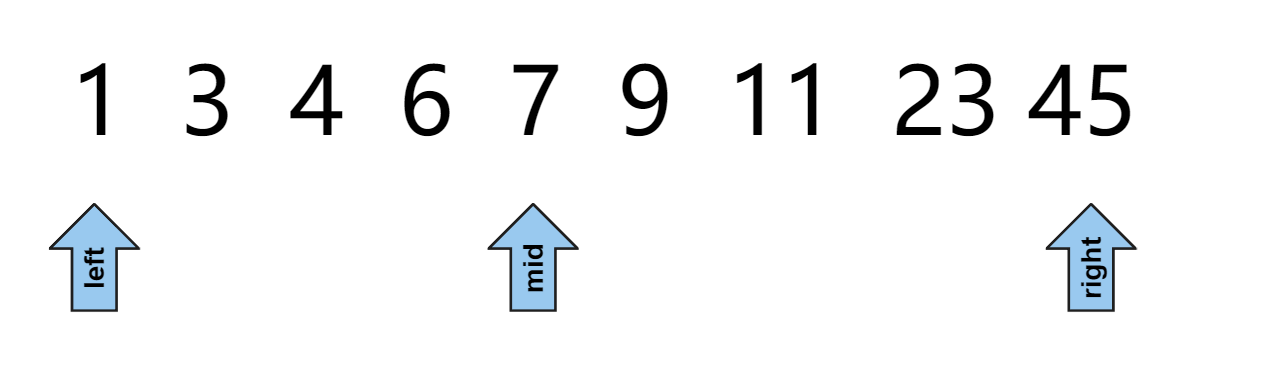
在这里插入图片描述
其实这样说是很不负责任的，什么时候停止？是left > right 还是left >= right ?

重要
有一个统一的标准很重要

这个统一的标准到底是啥呢，有两种方案可以选择：

边界自始至终都是有效的，left和right都是有意义的
左边界有意义，右边界无意义，或左边界无意义，右边界有意义

3.3 解决方案

方案一：边界都有效

如果左值left和右值right都有意义，那么我们在比较完mid和target之后，为保证新的left和right都有意义，对应要变换的边界就要跳过mid，如图：
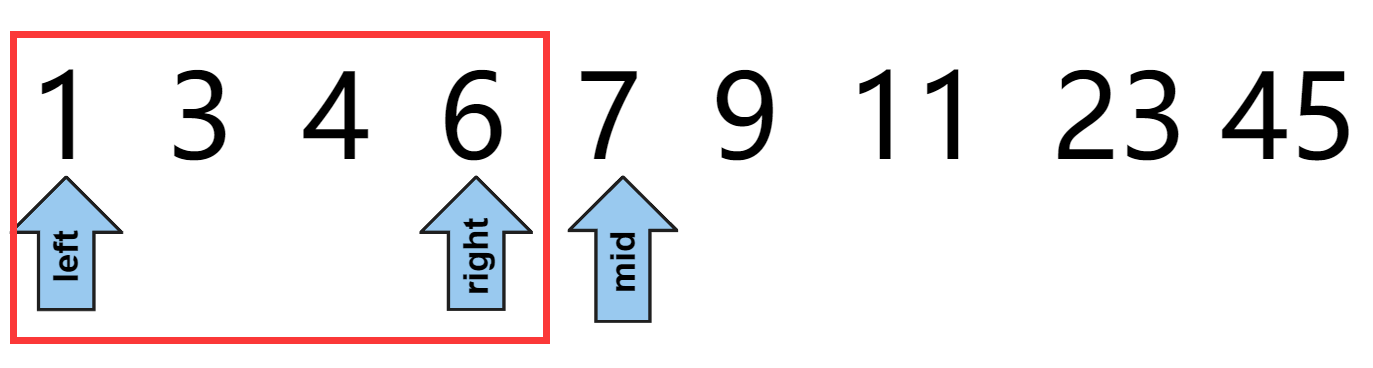
在这里插入图片描述

int right = numsSize - 1;//保证区间都是有效的 
while(left >= right)//既然有效就要二分查找
{
	    int mid = (left + right)/2;
        if(target == nums[mid])   return mid;
        
        //两次修正都要保证新的区间仍然有效
        if(target < nums[mid])    
            right = mid-1;    
        else        
            left = mid+1;        
}

方案二：有一个边界无效

如图，在最开始我们就让某一个区间无效，由于右区间较简单，因此采用右边界无效的方案

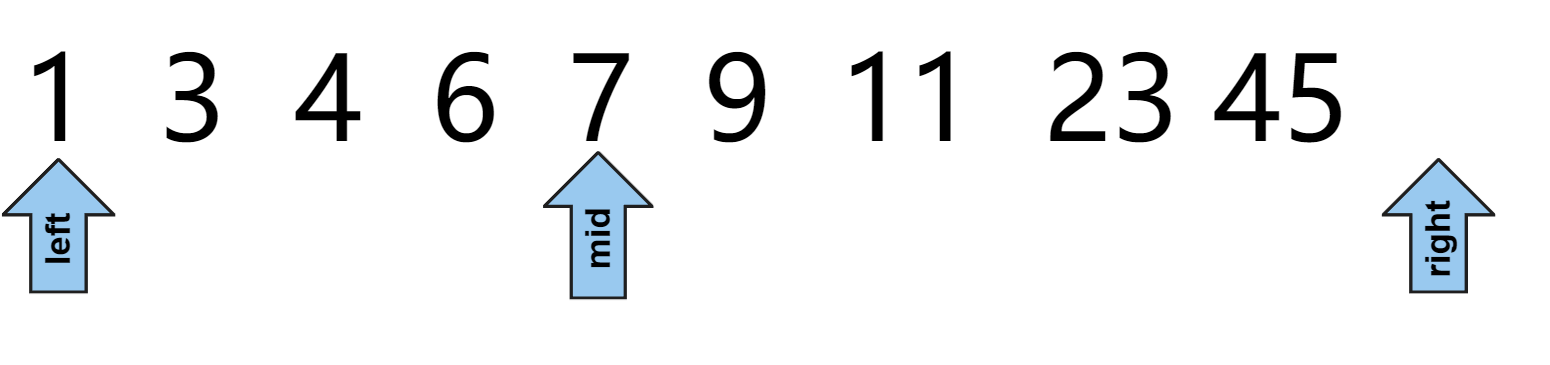
我们希望下一次缩小区间的时候，仍然是右区间无效，经过上一次mid与target比较后，我们已经清楚mid不是我们要找的，因此下一次调整区间，我们就可以让right直接到mid位置处，这样右区间仍然没有意义！
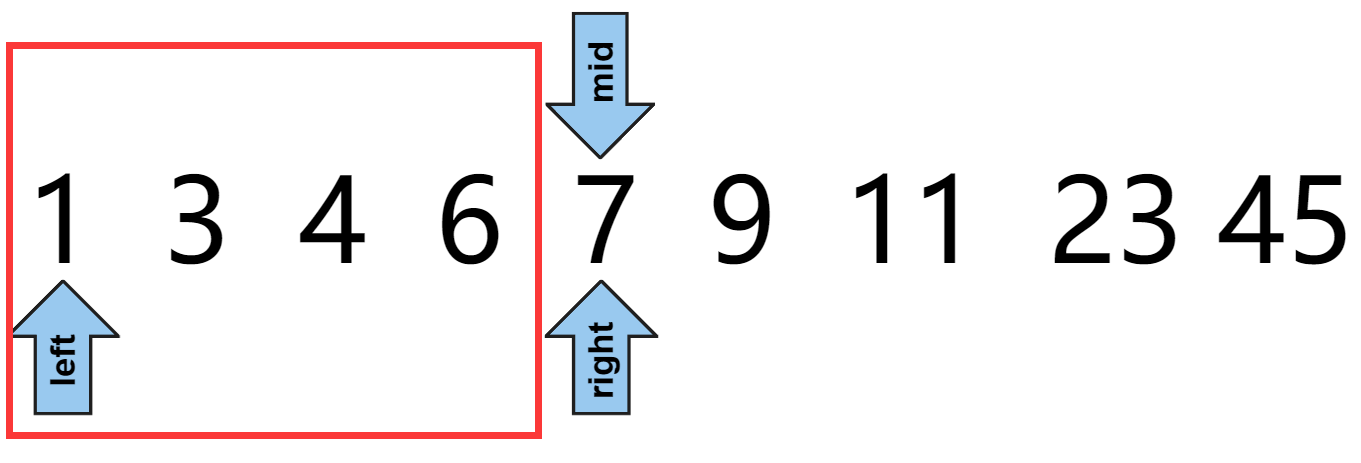
在这里插入图片描述

int right = numsSize;//保证右区间是无效的 
while(left > right)//等于是无效区间，不需要二分查找
{
	    int mid = (left + right)/2;
        if(target == nums[mid])   return mid;
        
        //两次修正都要保证新的区间仍然有效
        if(target < nums[mid])    
            right = mid;//保证新区间仍然是无效区间    
        else        
            left = mid+1;        
}

3.4参考代码

//方案一
int search(int* nums, int numsSize, int target){
    int left = 0;
    int right = numsSize-1;
    //int mid = 0;

    while(left <= right)
    {
        int mid = (left + right)/2;
        if(target == nums[mid])
        {
            return mid;
        }

        if(target < nums[mid])
        {
            right = mid-1;
        }
        else
        {
            left = mid+1;
        }
    }

    return -1;
}

//方案二
int search(int* nums, int numsSize, int target){
    int left = 0;
    int right = numsSize;


    while(left < right)
    {
        int mid = (left + right)/2;
        if(target == nums[mid])
        {
            return mid;
        }

        if(target < nums[mid])
        {
            right = mid;
        }
        else
        {
            left = mid+1;
        }
    }

    return -1;
}

3.5 总结

二分查找问题虽然较为简单，但对边界问题有着比较严格的要求，只有学会控制边界，才不会出现一些细节的错误，虽然二分查找的思维很简单，但细节决定成败，相信看到这里，你一定有所体悟

四、螺旋矩阵

讲解完二分查找，相信你对边界问题掌握的更好了，接下来你可以去挑战一下略有难度的螺旋矩阵了！

题目概述

点击做题：螺旋矩阵2

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
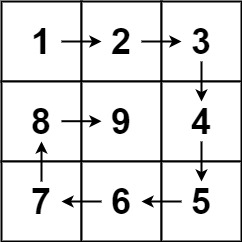
在这里插入图片描述

思路提示

同样的，我们要记住统一管理方案的原则，比如有四条边控制，我们应该怎么控制？
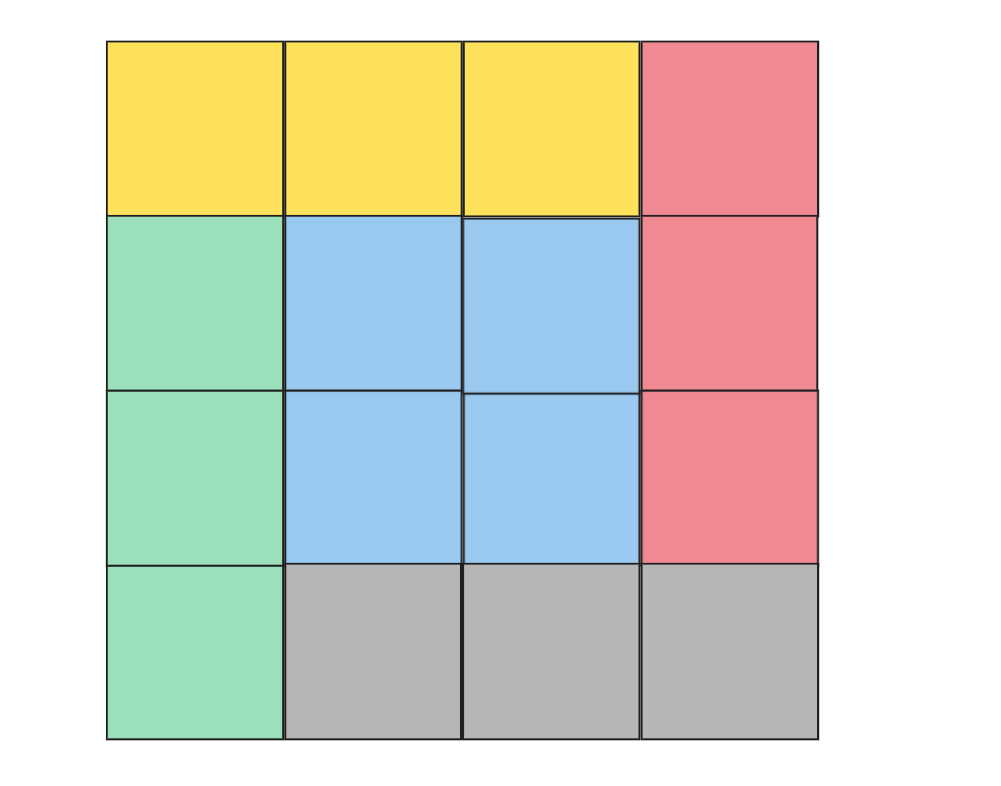
在这里插入图片描述
如图，第一行我们就只控制前三个，并且每一行或列都按照这个标准进行赋值，这样我们的边界就很难控制乱，第一行完成后，我们再去控制第二行，按照这样的标准一点点赋值

参考代码

int** generateMatrix(int n, int* returnSize, int** returnColumnSizes){

    *returnSize = n;
    *returnColumnSizes = (int*)malloc(sizeof(int) * n);

    int** result = (int**)malloc(sizeof(int*) * n);
    int i,j;
    for(i = 0; i < n; i++) {
        result[i] = (int*)malloc(sizeof(int) * n);
        (*returnColumnSizes)[i] = n;
    }

    int k = 1;
    int mid = n / 2;
    int startx = 0;
    int starty = 0;
    int offset = 1;
 
    int fre = n / 2;//一共要处理几层
    while(fre--)
    {       
        for(j = starty;j<n-offset;j++)
            result[startx][j] = k++;
        
        for(i = startx;i<n-offset;i++)
            result[i][j] = k++;
        
        for(;j>startx;j--)
            result[i][j] = k++;
        
        for(;i>starty;i--)
            result[i][j] = k++;
        
        startx++;
        starty++;
        offset++;
    }
   
    *returnSize = n;
    for(int i = 0;i<n;i++)
    {
        (*returnColumnSizes)[i] = n;
    }
   
   //单独判断是否为奇数个
    if(n%2){
        result[mid][mid] = k;
    }
    
    return result;
}