- 前言
- 一、背景知识
- 二、前序遍历
- 三、中序遍历
- 四、后序遍历
- 五、求二叉树中结点的个数
- - 1. 遍历+计数
  - - （1）前序遍历+计数
    - （2）中序遍历+计数
    - （3）后序遍历+计数
  - 2.分治算法思想（推荐）
敬请期待

前言

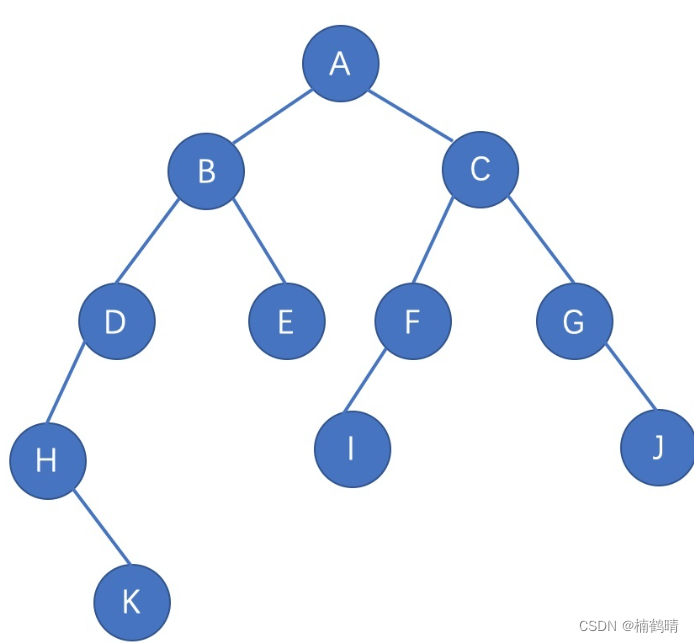
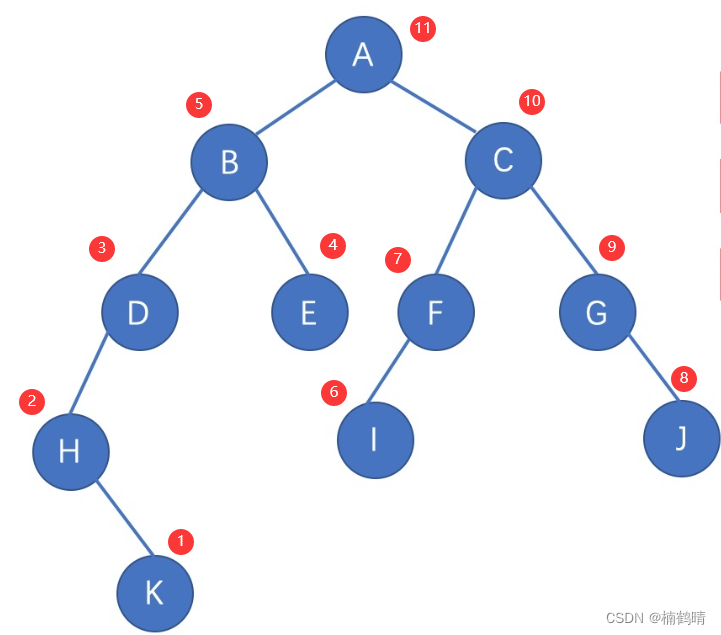
前面我们学习的数据结构主要是线性表，我们在学习的时候主要是学习对数据结构中的数据进行增删查改，但是我们会发现，对于普通的二叉树而言，插入一个数据可以在很多地方进行插入，删除数据也可以在很多地方进行删除，同样的道理，在没有一定规律的情况下，想要在普通的二叉树中进行查找数据也是很麻烦的，修改也是一样的道理，所以，学习普通二叉树的增删查改是没有任何意义的，今天我们重点学习的是二叉树的几种重要的遍历方式：前序遍历，中序遍历，后序遍历，层序遍历。其中，前面三种遍历方式需要我们对递归有一个很深层次的理解才能够搞懂！！！今天我们主要以下面这棵树作为例子进行讲解。

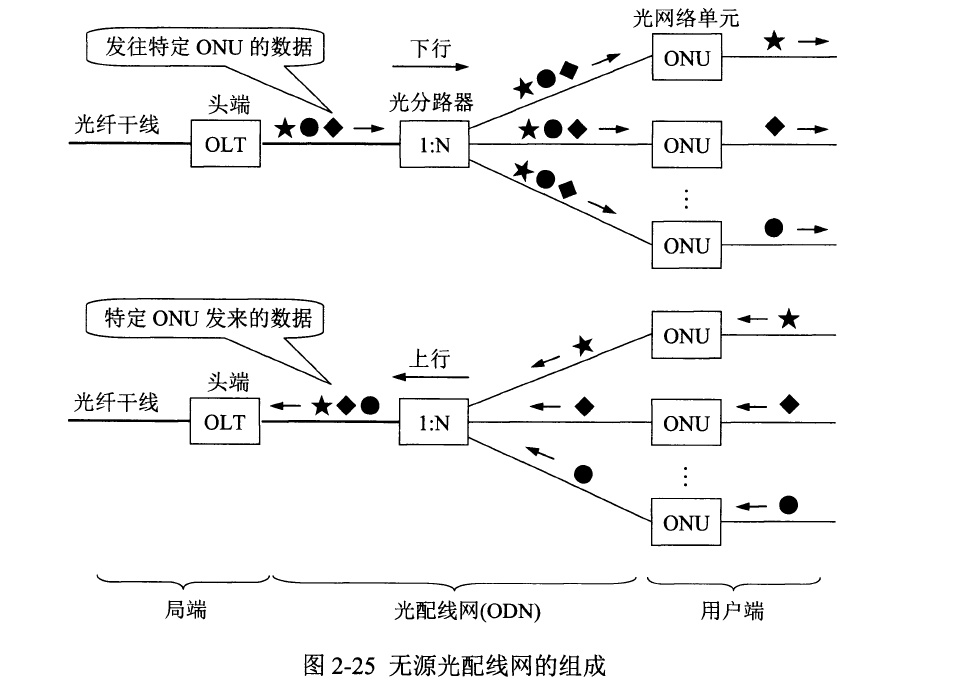
一、背景知识

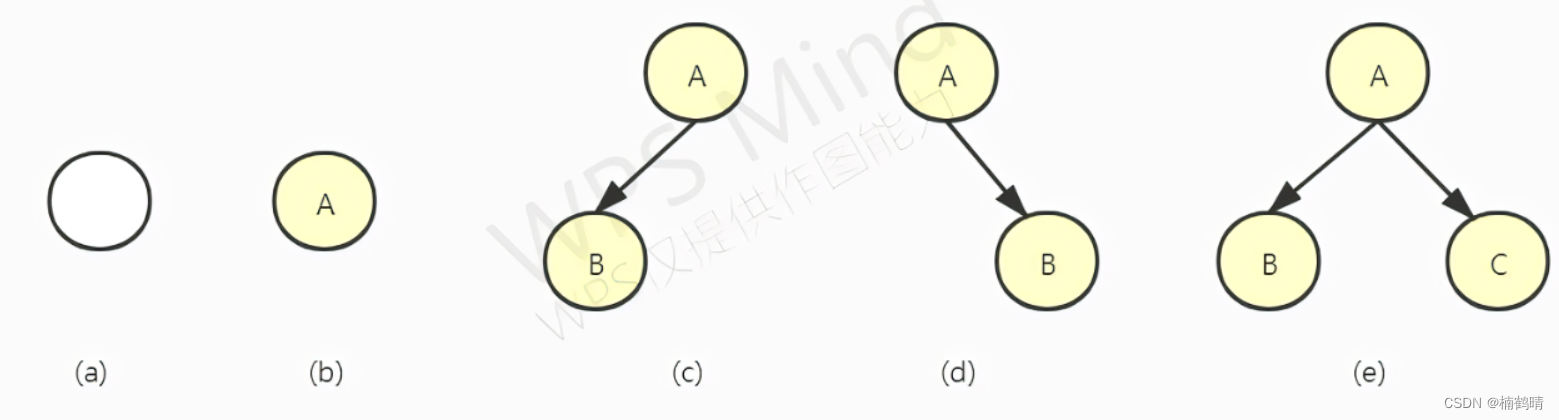
在学习二叉树的遍历之前我们需要知道，二叉树中可以分为很多的子树，每一棵子树都是由对应的根节点和左右子树组成的，其中根节点和左右子树都是有可能为空的，这个视具体情况而定。这个基本知识可以为后面学习递归和分治算法思想做很大的铺垫。任何的子树可能存在的情况为：空树，只有根节点，只有左子树，只有右子树，同时存在左右子树。

空树：即根节点为空指针的情况
只有根节点：根节点不为空，但是左右子树均为空
只有左子树：根节点和左子树不为空，右子树为空
只有右子树：根节点和右子树不为空，左子树为空
同时存在左右子树：根节点和左右子树均不为空

对应的就是下图的情况：
在这里插入图片描述

二、前序遍历

我们知道，树中的任何子树都是由根节点和左右子树构成的，对于每一棵子树而言，前序遍历方式的规则是：根节点，左子树，右子树。也就是说，我们可以将一棵树想象成很多的子树，我们在遍历一棵二叉树的时候，需要将所有的子树全部遍历完，而遍历方式就是规定了树中的遍历规则，即每一棵子树应该按照什么样的顺序去遍历访问。下面我们使用前序遍历的方式来详细介绍下图的遍历：
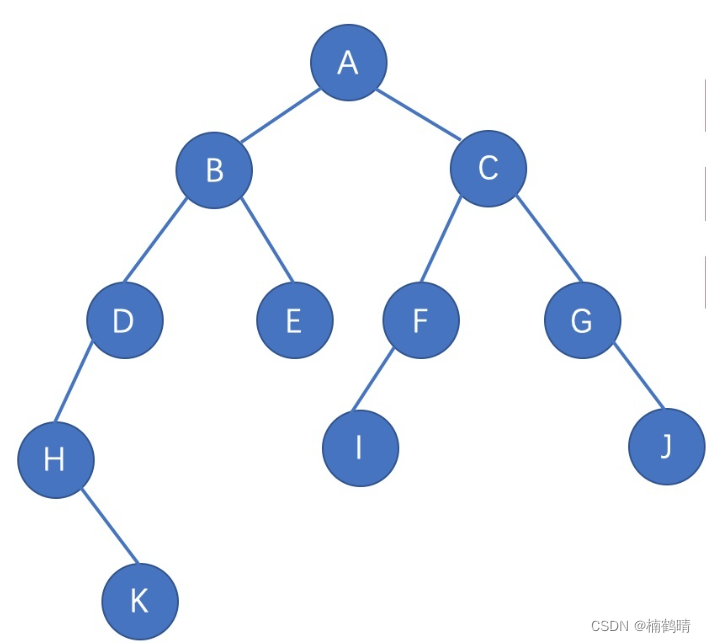
在这里插入图片描述

遍历过程：首先访问的是A结点对应的树，而A结点对应的树是由A结点和对应的左右子树构成的，根据前序遍历的方式，先访问的是A结点，然后访问A结点的左子树，A结点对应的左子树的根节点是B结点，所以接下来访问的就是B结点对应的树，B结点对应的树同样是由B结点和对应的左右子树构成，根据前序遍历的方式，先访问的是B结点，然后访问B结点的左子树，B结点对应的左子树就是D节点对应的树了，D结点对应的树是由D结点和对应的左右子树构成的，访问D结点的树时，先访问D结点，然后访问D结点对应的左子树，D结点对应的左子树是H结点对应的树，H结点对应的树同样是由D结点和对应的左右子树构成，访问H结点的树时先访问H结点，然后再访问H结点对应的左子树，我们会发现，当我们在访问H结点的左子树时，发现H结点的左子树是空，所以此时就会返回到H结点，此时对于H结点对应的树而言，H结点对应的树的根节点和左子树已经访问完成，所以接下来访问的就是H结点的右子树了，H结点的右子树是K结点对应的树，K结点对应的树是由K结点和对应的左右子树构成，访问K结点时，先访问的是K结点，然后访问K结点的树的左子树，访问K结点的左子树时，发现为空，所以此时应该访问K结点的右子树，发现也为空，所以此时会返回到H结点，H结点遍历完成，返回到D结点，此时相当于D结点的左子树遍历完成，所以接下来访问的是D结点的右子树，发现为空，返回到B结点，此时B结点对应的左子树访问完成，继续访问B结点的右子树，也就是E结点对应的树，E结点对应的树是由E结点和对应的左右子树构成，访问E树时，先访问E结点，再访问E树的左子树，访问E树的左子树时，发现为空，返回到E树，再访问右子树，发现为空，返回到B树，此时B树访问完成，也就是A树的左子树访问完成，接下来访问的就是A树的右子树了，情况和上面一样。

最后的遍历顺序为：
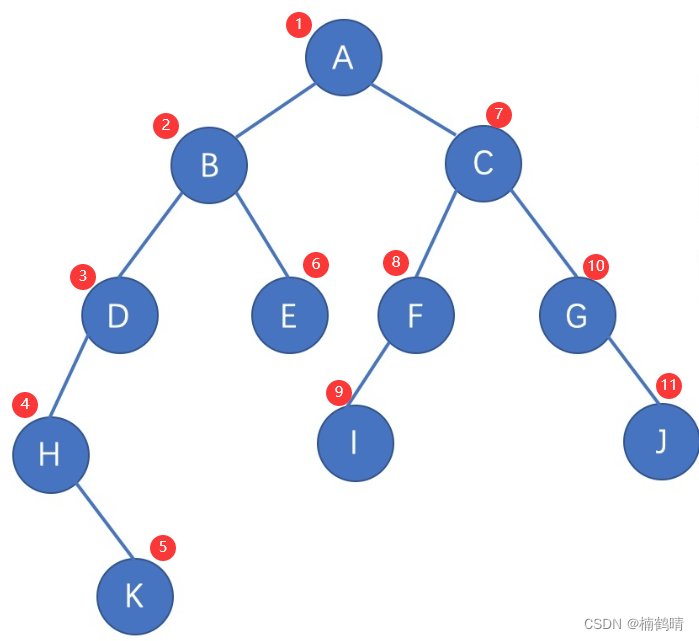
在这里插入图片描述
即：

代码实现

typedef int BTDataType;
// 链式二叉树的定义
typedef struct BinaryTreeNode
{
	BTDataType data;  // 数据域
	struct BinaryTreeNode* left;// 指向左子树的指针
	struct BinaryTreeNode* right;// 指向右子树的指针
}BTNode;

// 前序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

BTNode* CreateBinaryTree(BTDataType data)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		return NULL;
	}
	newnode->data = data;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}

int main()
{
// 手动创建树的结点
	BTNode* Node1 = CreateBinaryTree(1);
	BTNode* Node2 = CreateBinaryTree(2);
	BTNode* Node3 = CreateBinaryTree(3);
	BTNode* Node4 = CreateBinaryTree(4);
	BTNode* Node5 = CreateBinaryTree(5);
	BTNode* Node6 = CreateBinaryTree(6);
// 手动将创建的结点链接起来
	Node1->left = Node2;
	Node1->right = Node3;
	Node2->left = Node4;
	Node2->right = Node5;
	Node3->left = Node6;

	PrevOrder(Node1);
	return 0;
}

实验结果

根据上面对于前序遍历的分析，这里不难分析出这个结果。

三、中序遍历

中序遍历方式的规则是：左子树，根节点，右子树。注意在分析的过程是要将树分成很多子树进行访问的。这里同样以上面这棵树作为例子进行分析：
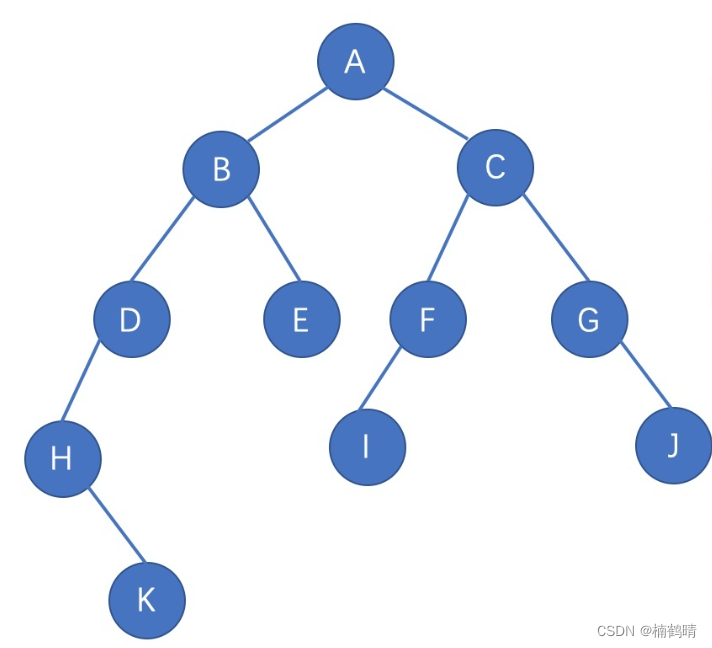
在这里插入图片描述

遍历过程：首先给到树的根节点，所以先访问到A树，但是访问A树时，需要先访问A树的左子树，所以接下来访问A树的左子树，A树的左子树是B树，访问B树时，需要先访问B树的左子树，接下来访问B树的左子树，B树的左子树是D树，访问D树时，需要先访问D树的左子树，D树的左子树是H树，访问H树时需要先访问H树的左子树，当我们访问H树的左子树时，我们发现H树的左子树是空树，所以直接返回到H树，那么H树的左子树访问完成之后就应该访问H树的根节点也就是H结点，H结点返回完之后返回H树的右子树，H树的右子树是K树，访问K树时需要先访问K树的左子树，当我们访问K树的左子树时，发现K树的左子树为空，所以返回到K树，继续访问K树的根节点，也就是K结点，再访问K树的右子树，K树的右子树为空，所以返回到H树，H树的右子树访问完成，返回到D树，D树的左子树访问完成，继续访问D树的根节点，也就是D结点，再访问D树的右子树，D树的右子树为空，返回到B树，B树的左子树访问完成，继续访问B树的根节点，也就是B结点，再访问B树的右子树，B树的右子树为E树，访问E树时需要先访问E树的左子树，E树的左子树为空，返回到E树，继续访问E树的根节点，也就是E结点，再访问E树的右子树，E树的右子树为空，返回到B树，B树的右子树访问完成，即B树访问完成，即A树的左子树访问完成，这个时候才可以访问A树的根节点，也就是A结点，再继续访问A树的右子树，访问A树的右子树的过程和访问A树的左子树一模一样。

最终的访问顺序为：
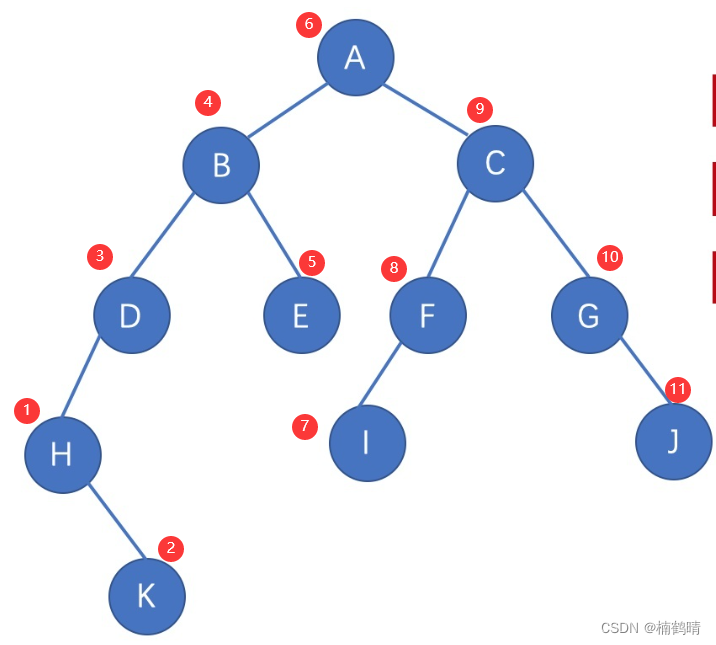
在这里插入图片描述
即：

代码实现

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

// 中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

BTNode* CreateBinaryTree(BTDataType data)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		return NULL;
	}
	newnode->data = data;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}

int main()
{
	BTNode* Node1 = CreateBinaryTree(1);
	BTNode* Node2 = CreateBinaryTree(2);
	BTNode* Node3 = CreateBinaryTree(3);
	BTNode* Node4 = CreateBinaryTree(4);
	BTNode* Node5 = CreateBinaryTree(5);
	BTNode* Node6 = CreateBinaryTree(6);

	Node1->left = Node2;
	Node1->right = Node3;
	Node2->left = Node4;
	Node2->right = Node5;
	Node3->left = Node6;

	InOrder(Node1);
	return 0;
}

实验结果

四、后序遍历

后序遍历的规则是：左子树，右子树，根节点。
在遍历的过程中同样需要将待分析的树分成很多的子树，然后依次分析每棵子树的访问，访问每一棵子树的时候，都需要知道每一棵子树都是由根节点和左右子树构成，根据后序遍历的规则，需要先遍历左子树，再遍历右子树，最后遍历根节点。这里同样以上面这棵树作为例子进行分析：
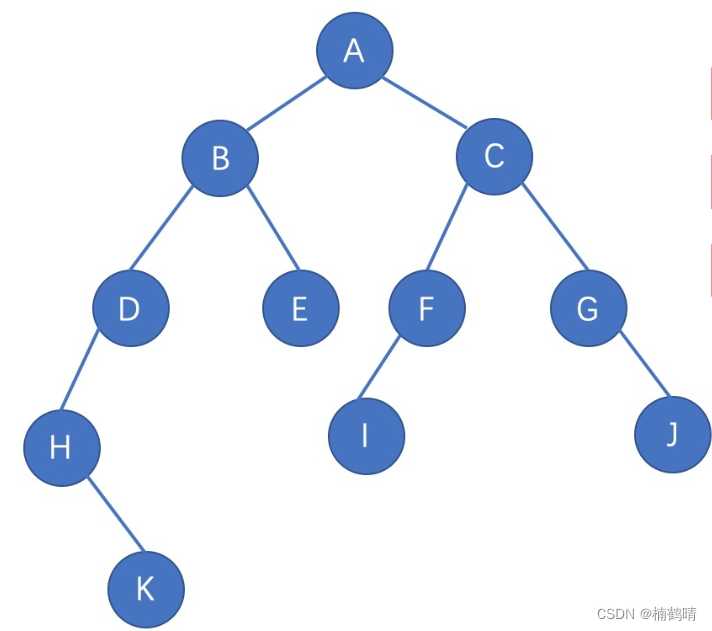
在这里插入图片描述

遍历过程：首先给到的条件是树的根节点，所以肯定从根节点进行分析，首先访问A树，访问A树时，需要先访问A树的左子树，A树的左子树是B树，访问B树时需要先访问B树的左子树，B树的左子树是D树，访问D树时，需要先访问D树的左子树，D树的左子树是H树，访问H树时，需要先访问H树的左子树，H树的左子树是空树，所以返回到H树，继续访问H树的右子树，H树的右子树是K树，访问K树时，先访问K树的左子树，K树的左子树是空树，返回到K树，继续访问K树的右子树，K树的右子树为空树，返回到K树，再访问K树的根节点，也就是K结点，K树访问完成之后，H树的右子树访问完成，继续访问H树的根节点，也就是H结点，H树访问完成之后，相当于D树的左子树访问完成，继续访问D树的右子树，D树的右子树为空，返回到D树，继续访问D树的根节点，也就是D结点，D树访问完成之后，相当于B树的左子树访问完成，继续访问B树的右子树，B树的右子树是E树，访问E树时，需要先访问E树的左子树，E树的左子树是空，返回到E树，继续访问E树的右子树，E树的右子树为空，返回到E树，继续访问E树的根节点，也就是E结点，E树访问完成之后，相当于B树的右子树访问完成，返回到B树，继续访问B树的根节点，也就是B结点，B树访问完成之后，相当于A树的左子树访问完成，然后继续访问A树的右子树，访问过程和访问A树的左子树一模一样，当A树的右子树访问完成之后，最后再继续访问A树的根节点，也就是A结点，当A树访问完成之后，整棵树的遍历即完成。

最终的访问顺序为：

即：
代码实现：

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

// 后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

BTNode* CreateBinaryTree(BTDataType data)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		return NULL;
	}
	newnode->data = data;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}

int main()
{
	BTNode* Node1 = CreateBinaryTree(1);
	BTNode* Node2 = CreateBinaryTree(2);
	BTNode* Node3 = CreateBinaryTree(3);
	BTNode* Node4 = CreateBinaryTree(4);
	BTNode* Node5 = CreateBinaryTree(5);
	BTNode* Node6 = CreateBinaryTree(6);

	Node1->left = Node2;
	Node1->right = Node3;
	Node2->left = Node4;
	Node2->right = Node5;
	Node3->left = Node6;

	PostOrder(Node1);
	return 0;
}

实验结果：

五、求二叉树中结点的个数

1. 遍历+计数

（1）前序遍历+计数

代码实现

// 求结点个数
int count = 0;
void TreeNodeSize1(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	// 前序遍历
	count++;
	TreeNodeSize1(root->left);
	TreeNodeSize1(root->right);
}

int main()
{
	BTNode* Node1 = CreateBinaryTree(1);
	BTNode* Node2 = CreateBinaryTree(2);
	BTNode* Node3 = CreateBinaryTree(3);
	BTNode* Node4 = CreateBinaryTree(4);
	BTNode* Node5 = CreateBinaryTree(5);
	BTNode* Node6 = CreateBinaryTree(6);

	Node1->left = Node2;
	Node1->right = Node3;
	Node2->left = Node4;
	Node2->right = Node5;
	Node3->left = Node6;

	TreeNodeSize1(Node1);
	printf("TreeNodeSize:%d\n", count);
	return 0;
}

实验结果

（2）中序遍历+计数

代码实现

// 求结点个数
void TreeNodeSize2(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	// 中序遍历
	
	TreeNodeSize2(root->left);
	count++;
	TreeNodeSize2(root->right);
}

int main()
{
	BTNode* Node1 = CreateBinaryTree(1);
	BTNode* Node2 = CreateBinaryTree(2);
	BTNode* Node3 = CreateBinaryTree(3);
	BTNode* Node4 = CreateBinaryTree(4);
	BTNode* Node5 = CreateBinaryTree(5);
	BTNode* Node6 = CreateBinaryTree(6);

	Node1->left = Node2;
	Node1->right = Node3;
	Node2->left = Node4;
	Node2->right = Node5;
	Node3->left = Node6;

	TreeNodeSize2(Node1);

	printf("TreeNodeSize:%d\n", count);
	return 0;
}

实验结果

（3）后序遍历+计数

代码实现

// 求结点个数
void TreeNodeSize3(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	// 后序遍历

	TreeNodeSize3(root->left);
	TreeNodeSize3(root->right);
	count++;
}

int main()
{
	BTNode* Node1 = CreateBinaryTree(1);
	BTNode* Node2 = CreateBinaryTree(2);
	BTNode* Node3 = CreateBinaryTree(3);
	BTNode* Node4 = CreateBinaryTree(4);
	BTNode* Node5 = CreateBinaryTree(5);
	BTNode* Node6 = CreateBinaryTree(6);

	Node1->left = Node2;
	Node1->right = Node3;
	Node2->left = Node4;
	Node2->right = Node5;
	Node3->left = Node6;


	TreeNodeSize3(Node1);

	printf("TreeNodeSize:%d\n", count);
	return 0;
}

实验结果

注意：
上面三种遍历+计数的方式虽然通过上面的测试可以计算出二叉树中结点的个数，但是如果多次调用就会出现一些问题，我们以前序为例：

int main()
{
	BTNode* Node1 = CreateBinaryTree(1);
	BTNode* Node2 = CreateBinaryTree(2);
	BTNode* Node3 = CreateBinaryTree(3);
	BTNode* Node4 = CreateBinaryTree(4);
	BTNode* Node5 = CreateBinaryTree(5);
	BTNode* Node6 = CreateBinaryTree(6);

	Node1->left = Node2;
	Node1->right = Node3;
	Node2->left = Node4;
	Node2->right = Node5;
	Node3->left = Node6;


	 TreeNodeSize1(Node1);
	 printf("TreeNodeSize:%d\n", count);

	TreeNodeSize1(Node1);
	printf("TreeNodeSize:%d\n", count);

	TreeNodeSize1(Node1);
	printf("TreeNodeSize:%d\n", count);
	return 0;
}

实验结果

我们会发现，上面的结果显然被累加了，所以结果显然是错误，因为我们是通过一个全局变量的计数器count来计数二叉树中结点的个数，所以我们每次在进行计数之前需要对计数器进行清零，防止累加。
代码实现

int main()
{
	BTNode* Node1 = CreateBinaryTree(1);
	BTNode* Node2 = CreateBinaryTree(2);
	BTNode* Node3 = CreateBinaryTree(3);
	BTNode* Node4 = CreateBinaryTree(4);
	BTNode* Node5 = CreateBinaryTree(5);
	BTNode* Node6 = CreateBinaryTree(6);

	Node1->left = Node2;
	Node1->right = Node3;
	Node2->left = Node4;
	Node2->right = Node5;
	Node3->left = Node6;

	count = 0;
	 TreeNodeSize1(Node1);
	printf("TreeNodeSize:%d\n", count);
	
	count = 0;
	TreeNodeSize1(Node1);
	printf("TreeNodeSize:%d\n", count);

	count = 0;
	TreeNodeSize1(Node1);
	printf("TreeNodeSize:%d\n", count);
	return 0;
}

实验结果

2.分治算法思想（推荐）

分治算法思想的本质其实也是一种递归的算法思想，其原理是通过将原来的问题分解为子问题，直到不能再分解为止。
像在使用分治算法思想求解二叉树的结点个数时，我们可以将求解的结点个数转换成：待求树的左子树的结点个数+右子树的结点个数+根节点，树中的每一棵子树都是采用这种递归的形式进行求解，直到递归到叶子节点时，叶子节点的左右子树均是空，此时返回的就是叶子结点本身的个数，也就是1，然后依次返回，最终即可求得结果。

代码实现

// 求结点个数
size_t TreeNodeSize4(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return TreeNodeSize4(root->left) + TreeNodeSize4(root->right) + 1;

int main()
{
	BTNode* Node1 = CreateBinaryTree(1);
	BTNode* Node2 = CreateBinaryTree(2);
	BTNode* Node3 = CreateBinaryTree(3);
	BTNode* Node4 = CreateBinaryTree(4);
	BTNode* Node5 = CreateBinaryTree(5);
	BTNode* Node6 = CreateBinaryTree(6);

	Node1->left = Node2;
	Node1->right = Node3;
	Node2->left = Node4;
	Node2->right = Node5;
	Node3->left = Node6;

	
	printf("TreeNodeSize:%zu\n", TreeNodeSize4(Node1));

	
	return 0;
}
}