- 💭 写在前面:本文旨在探讨不可变数据结构在 F# 编程中的应用,特别是如何利用递归记录类型来表示和操作数值表达式。通过定义存储整数的二叉树和数值表达式的类型,我们将展示不可变性如何简化程序的理解和维护。文章将对比 F# 与命令式编程语言(如 C 和 C++)在处理类似问题时的差异,强调 F# 不可变性的优势,并通过示例展示如何在 F# 中对表达式求值
目录
0x00 递归类型(Recursive Type)
0x01 关于 “值一旦定义就不会改变” 特性
0x01 举例:语法树
0x00 递归类型(Recursive Type)
让我们定义一个存储整数的(完整的)二叉树,归纳类型定义如下:
- 基本情况 (Base case):单个叶子是一个二叉树
- 归纳情况 (Inductive case):一个拥有两个子树的节点也是一棵树
type Tree = Leaf of int | Node of int * Tree * Tree
let t1: Tree = Node (3, Leaf 1, Leaf 2)
let t2: Tree = Node (5, Leaf 4, t1)
注意不可变性!在前面的例子中,如果我们将 更新为一个新值,会发生什么?这会影响
吗?
这是我们在命令式编程语言中所期望的,我们必须始终考虑内存状态和指针。
let t1 = Node (3, Leaf 1, Leaf 2)
let t2 = Node (5, Leaf 4, t1)
let t1 = Leaf 7 // 会发生What?t2会不会变?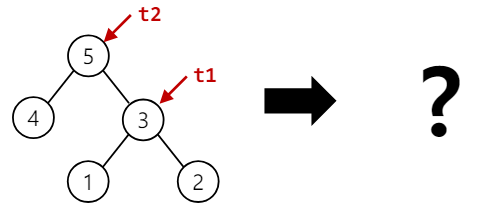
在 F# 中,一旦定义了值,它们就不会改变!(就像在数学中一样)
实际上,你并没有更新 ,你正在定义一个新值(Leaf 7)并给它一个名称
。因此,我们不必关心内存状态的 "副作用":
let t1 = Node (3, Leaf 1, Leaf 2)
let t2 = Node (5, Leaf 4, t1)
let t1 = Leaf 7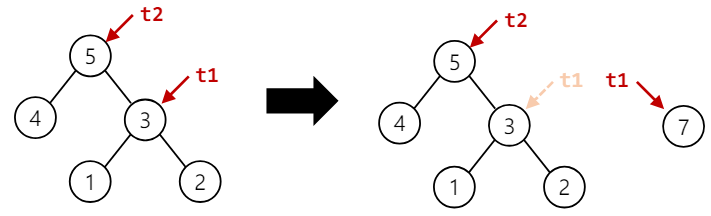
0x01 Immutability 特性(不可变特性)
"值一旦定义就不会改变"
这实际上是 F# 的核心特性,也挺好的,至少我们不必担心某个值在程序的其他地方被意外地修改。
let x = 12
let y = x + 1x 被定义为 12,y 被定义为 x + 1,即 13,也不会被改变。
如果我们需要表示和操作类似于你在问题中提到的数值表达式,可以使用 可辨识联合类型:
type Exp =
| Num of int
| Var of string
| Add of Exp * Exp
| Sub of Exp * Exp
| Mul of Exp * Exp
| Div of Exp * Exp
let e = Mul (Num 3, Add (Var "x", Num 1))这个 Exp 就是一个 递归记录类型 (discriminated union),它可以是一个整数,一个变量,或者是两个表达式相加、相减、相乘或者相除。
每一个 Exp 类型的值都是不可变的。一旦你创建了 e,它的结构和值都不能改变。
这种不可变性有助于编写健壮且容易理解的代码。
为了演示如何在 F# 中对这种表达式求值,我们举个例子。
假设我们有一个上下文(例如,一个字典)来存储变量的值:
let rec eval (exp: Exp) (context: Map<string, int>) =
match exp with
| Num n -> n
| Var v -> context.[v]
| Add (e1, e2) -> eval e1 context + eval e2 context
| Sub (e1, e2) -> eval e1 context - eval e2 context
| Mul (e1, e2) -> eval e1 context * eval e2 context
| Div (e1, e2) -> eval e1 context / eval e2 context
// 创建一个上下文
let context = Map.ofList [("x", 2)]
// 计算表达式 e 的值
let result = eval e context
printfn "The result of the expression is %d" result这就展示了如何在 F# 中处理不可变的数据结构,并使用递归函数来操作这些数据结构。
eval 是一个递归函数,接受一个表达式和一个上下文(变量值的映射)。
根据表达式的类型进行模式匹配,并计算出结果。
字典中存储了 ,通过 eval e context 计算出表达式
的值为
0x01 举例:语法树
让我们定义一个类型来表示数值表达式,我们在讲座中已经看到了一个类似的语言定义,附带问题:我们如何在 C 或 C++ 中表示这种类型?
type Exp =
Num of int
| Var of string
| Add of Exp * Exp
| Sub of Exp * Exp
| Mul of Exp * Exp
| Div of Exp * Exp
let e = Mul (Num 3, (Add (Var "x", Num 1)) 的语法树:

在 C/C++中,我们可以使用结构体来表示这个类型,然后通过指针来建立树形结构。
#include <iostream>
#include <string>
struct Exp {
enum class Type {
NUM,
VAR,
ADD,
SUB,
MUL,
DIV
};
Type type;
int numValue; // 仅在类型为 NUM 时有效
std::string varName; // 仅在类型为 VAR 时有效
Exp* left; // 左子表达式
Exp* right; // 右子表达式
};
// 创建一个新的表达式节点
Exp* makeNum(int value) {
Exp* exp = new Exp;
exp->type = Exp::Type::NUM;
exp->numValue = value;
exp->left = nullptr;
exp->right = nullptr;
return exp;
}
Exp* makeVar(const std::string& name) {
Exp* exp = new Exp;
exp->type = Exp::Type::VAR;
exp->varName = name;
exp->left = nullptr;
exp->right = nullptr;
return exp;
}
Exp* makeAdd(Exp* left, Exp* right) {
Exp* exp = new Exp;
exp->type = Exp::Type::ADD;
exp->left = left;
exp->right = right;
return exp;
}
Exp* makeSub(Exp* left, Exp* right) {
Exp* exp = new Exp;
exp->type = Exp::Type::SUB;
exp->left = left;
exp->right = right;
return exp;
}
Exp* makeMul(Exp* left, Exp* right) {
Exp* exp = new Exp;
exp->type = Exp::Type::MUL;
exp->left = left;
exp->right = right;
return exp;
}
Exp* makeDiv(Exp* left, Exp* right) {
Exp* exp = new Exp;
exp->type = Exp::Type::DIV;
exp->left = left;
exp->right = right;
return exp;
}
// 释放表达式树的内存
void freeExp(Exp* exp) {
if (exp) {
freeExp(exp->left);
freeExp(exp->right);
delete exp;
}
}
int main() {
// 创建示例表达式
Exp* e = makeMul(makeNum(3), makeAdd(makeVar("x"), makeNum(1)));
// 打印表达式类型
switch (e->type) {
case Exp::Type::NUM:
std::cout << "Num: " << e->numValue << std::endl;
break;
case Exp::Type::VAR:
std::cout << "Var: " << e->varName << std::endl;
break;
case Exp::Type::ADD:
std::cout << "Add" << std::endl;
break;
case Exp::Type::SUB:
std::cout << "Sub" << std::endl;
break;
case Exp::Type::MUL:
std::cout << "Mul" << std::endl;
break;
case Exp::Type::DIV:
std::cout << "Div" << std::endl;
break;
}
// 释放内存
freeExp(e);
return 0;
}我们使用了一个结构体来表示表达式的不同部分,并且定义了函数来创建和释放表达式树。这样可以在内存中构建出一个对应于给定表达式的树形结构,并且能够在使用完后释放这些内存。

📌 [ 笔者 ] 王亦优
📃 [ 更新 ] 2024.6.5
❌ [ 勘误 ] /* 暂无 */
📜 [ 声明 ] 由于作者水平有限,本文有错误和不准确之处在所难免,
本人也很想知道这些错误,恳望读者批评指正!| 📜 参考资料 Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. . |