下面来看三句话:
(1)一个数的补码等于原码取反加1
(2)减去一个数等于加这个数的补码
(3)一个数的反码就是这个数原码的每一位都取反
学过补码的同学应该都听过类似的表述,如果你觉得这三句话都对,那说明你还没有真的理解补码。
其实这三句话都是错的!下边来分析一下。
目录
1、计算机的运算器基本运行原理
2、无符号数和有符号数
3、模的概念
4、正数和负数的意义
5、减法的意义
6、反码和补码的意义
7、求负数补码的三种方法
(1)原码除符号位取反加1
(2)负数相反数所有位取反(含符号位)加1
(3)模+负数的结果,然后转成二进制编码,符号位为1
8、结论
1、计算机的运算器基本运行原理
计算机的硬件都是依据冯诺依曼体系架构的,硬件主要由运算器、控制器、存储器、输入设备、输出设备五大部分构成。而现代计算机在实际制造时,运算器和控制器是合二为一的,也叫中央处理单元(CPU)。在嵌入式产品中,甚至把运算器、控制器、存储器、输入设备接口、输出设备接口五大部分都合到一起,叫做单片机。
其中运算器也叫算数逻辑单元ALU(arithmetic and logic unit),主要负责算数运算、逻辑运算和移位运算。在算数运算这个模块中,可以实现加、减、乘、除的算数运算,而实际在硬件设计时,最基本的运算只有加法运算电路。减法是转化为加法运算的,减去一个正数等于加上这个数的相反数(负数)。而乘法和除法是通过移位运算和加法运算实现的。
2、无符号数和有符号数
运算器要进行运算的数实际都是以二进制编码形式存在的,编码本身没有正负之分,正负是人为规定的。下边介绍两个概念:无符号数和有符号数。
无符号数,就是数的二进制编码不包含符号位,所有的位都用来编码表示数,无符号数只有0和正数。
有符号数,就是数的二进制编码最高位是符号位,符号位为1,代表这个数是负数,符号位为0,代表这个数为正数或0。
例如,对于一个8位的二进制数。如果是无符号数,那么这个数的范围是0~255,一共256个数。如果是有符号数,那么这个数的范围是-128~127,也是256个数。有符号数最高位为符号位,除去最高位,其他7位编码范围为0000000~1111111,当最高位为0时,编码范围为00000000~01111111,代表0~127,一共128个数。当最高位位1时,编码范围为10000000~11111111,代表-128~-1,也是128个数。负数和非负数加起来一共是256个数。
注意对于8位有符号数来说,00000000代表0,而10000000不代表0,代表-128,后边会介绍。
3、模的概念
计算机中数的二进制编码有原码、反码和补码三种,数的存储和运算都是以反码形式进行的。
补码和反码的设计主要是为了解决有符号数的负数在计算机中的表示和运算问题。补码和反码能够使得计算机中的减法运算转换为加法运算,从而简化了计算机硬件设计。而对于正数,由于其不存在减法运算中的借位问题,因此其原码、反码和补码可以保持一致,以方便计算机处理。
要想搞清楚反码和补码的概念,先介绍一下“模”的概念:“模”是指一个计量系统的计数范围,如过去计量粮食用的斗、时钟等。计算机也可以看成一个计量机器,因为计算机的字长是定长的,即存储和处理的位数是有限的,因此它也有一个计量范围,即都存在一个“模”。如:时钟的计量范围是0~11,模=12。表示n位的计算机计量范围是,模=
。“模”实质上是计量器所能装的最大量,当计量器里所装的东西一达到最大量时,这个计量器就封装起来拿走了(也就是溢出),所以模的值在计量器上表示不出来,计量器上只能表示出模的余数,也就是不满时候的量。
4、正数和负数的意义
为了更好理解,我们把模这个计量器看成纸箱,里边装的东西是苹果。
对于有符号数来说,这种纸箱有两个,大小相同,一个初始状态是空的,用来往里装苹果,里边装的苹果的数目就是数值的大小;另外一个纸箱初始状态是满的,用来往出拿苹果,里边剩余苹果的数目就是数值的大小。为了区分两个纸箱,用0标志还没满过的用来装苹果的纸箱,用1标志曾经满过用来往出拿苹果的纸箱。0和1就是纸箱的符号位。
正数,相当于往纸箱里装东西,装的过程中,纸箱不能达到满的状态,因为一达到满的状态,纸箱得封装起来了,纸箱外余下的苹果就是0了。所以对于8位二进制数来说,最高位为0时的范围为0~127。
负数,相当于从已经满了的纸箱中往出拿苹果,拿的过程中,不能拿0个,因为如果什么都不拿,纸箱还是满的,不能开封,我们看不到里边的苹果。所以,对于8位二进制数来说,最高位为1时的范围是-128~-1。
对于无符号数来说,这个纸箱只有一个,大小是有符号数纸箱的2倍。这个纸箱只用来装苹果,而不往出拿。这就是为什么如果某个变量只有正,没有负的情况时,我们要把数据类型声明为无符号类型(unsigned),因为无符号的纸箱更大,放的苹果更多。如果声明为默认的有符号数据类型,纸箱虽然有两个,但有一个从来不用,用到的那个只有一半大了。
5、减法的意义
知道了正数和负数的意义,之后来看一下减法的意义。
例如要求20-10这个结果,可以先把20-10变为20+(-10)。这个问题可以看成有两箱苹果,一个是空纸箱里放入了20个苹果,一个是从满的纸箱里取出10个苹果,然后把两个纸箱里的苹果合到一起,如果苹果满箱了(溢出),那就把装满一箱的苹果拿走,剩余的不满箱的苹果就是20-10的结果。
所以20-10=20+(-10)=20+128-10=138,因为138>128,已经满箱溢出,因此最终结果=138-128=10。
那么在计算机中,这个过程是怎么计算的呢,那就要用到反码和补码了。
6、反码和补码的意义
对于减法来说,就是从装满苹果的纸箱中往出拿苹果。假设要拿走10个苹果,也就是减10。反码就是纸箱打开时所能看到的最多苹果数目减去10。8位有符号数纸箱最多能装128个苹果,至少先拿走1个苹果,纸箱才能打开,所以打开纸箱能看到的苹果最多为127个。所以反码=127-10=117。而纸箱中实际还剩余苹果数量=128-10=118个,比反码多1个,这个实际的数目就是补码。因为求反码就是除符号位之外,把原码其他位取反即可,更容易计算,所以要先求反码,再加1,求出补码。反码是求补码的过渡码。
特别要注意:正数的反码、补码和原码一样;0的反码和补码都是是00000000,负数的反码就是除符号位外其他各位取反,负数的补码就是反码加1,如图1所示。
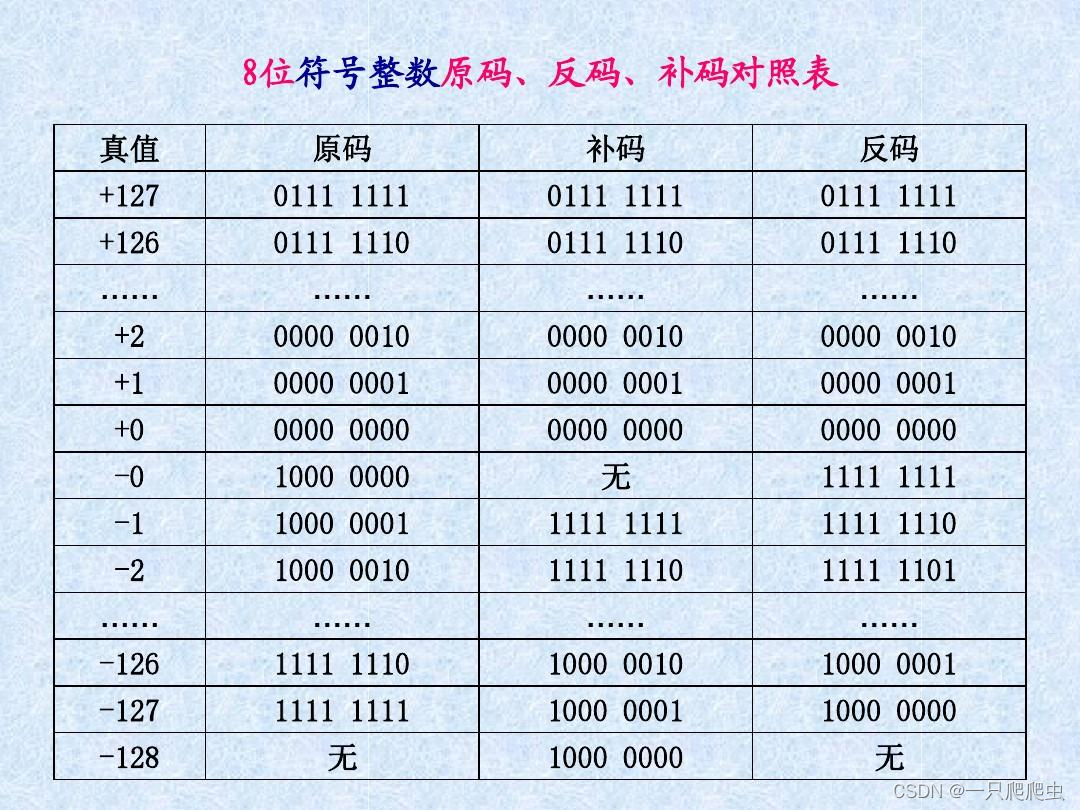
因为计算机中,数都是以补码存储的,所以
注意在计算20-10的过程中,不是求的10的补码,而是求的-10的补码,也就是减数的相反数的补码。
还要注意两点:
第一、两个数的运算实际上是以两个数的补码形式进行运算的。
第二、求负数的反码和补码过程不考虑符号位,而在两个补码运算过程中符号位是要参加运算的,不用考虑符号位是正还是负。也就是,求完两个数的补码后,两个补码连同符号位直接进行运算,就能得到正确结果了。
7、求负数补码的三种方法
以8位的有符号数-10为例:
(1)原码除符号位取反加1
-10的二进制原码为10001010,除符号位外取反后为11110101,加1为11110110,所以-10的补码为二级制数11110110。
(2)负数相反数所有位取反(含符号位)加1
-10的相反数为10,10的二进制编码为00001010,所有位取反为11110101,加1为11110110,所以-10的补码为二级制数11110110。
(3)模+负数的结果,然后转成二进制编码,符号位为1
8位有符号数的模为=128,模+(-10)=128-10=118,转化为二进制数为01110110,符号位置1为11110110,所以-10的补码为二级制数11110110。
三种方法得到的结果一样,第2种方法似乎比传统的第1种方法更快捷,如果这个负数比较大,那么第3种方法会更快捷。
8、结论
所以文章开始的那三句话准确的应该表述为:
(1)一个负数的补码等于原码取反(符号位不变)加1,非负数的补码等于原码
(2)减去一个数等于加这个数的相反数的补码
(3)一个负数的反码就是这个数原码的每一位都取反,其中符号位不变,非负数的反码等于原码。
(全文结束)