参考资料:活用pandas库
创建模型是持续性活动。当向模型中添加或删除变量时,需要设法比较模型,并需要统一的方法衡量模型的性能。
1、残差
模型的残差指实际观测值与模型估计值之差。
# 导入pandas库
import pandas as pd
# 读取数据集
housing=pd.read_csv(r"...\data\housing_renamed.csv")
# 展示数据
print(housing.head())
# 拟合一个多元线性回归模型
import statsmodels
import statsmodels.api as sm
import statsmodels.formula.api as smf
house1=smf.glm("value_per_sq_ft~ units+ sq_ft + boro",data=housing).fit()
print(house1.summary())
# 绘制模型残差
import seaborn as sns
import matplotlib.pyplot as plt
fig,ax=plt.subplots()
ax=sns.regplot(x=house1.fittedvalues,y=house1.resid_deviance,fit_reg=False)

(1)绘制残差散点图
# 通过boro变量为图着色。
res_df=pd.DataFrame({
'fittedvalues':house1.fittedvalues,
'resid_deviance':house1.resid_deviance,
'boro':housing['boro']
})
fig=sns.lmplot(x='fittedvalues',
y='resid_deviance',
hue='boro',
data=res_df,
fit_reg=False)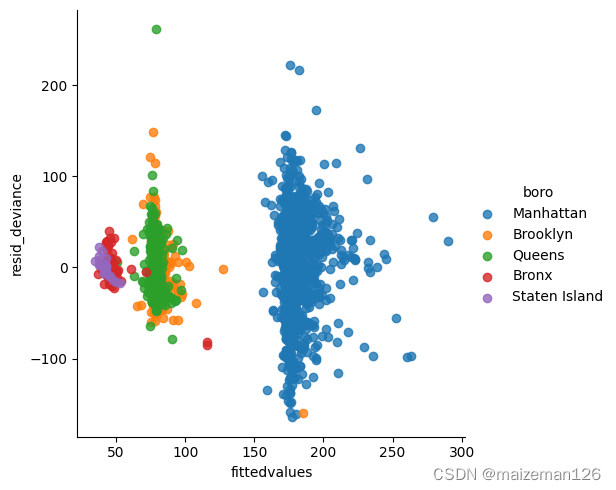
通过上图可见,当通过boro为点着色时,图中点簇收到了变量值的极大影响。
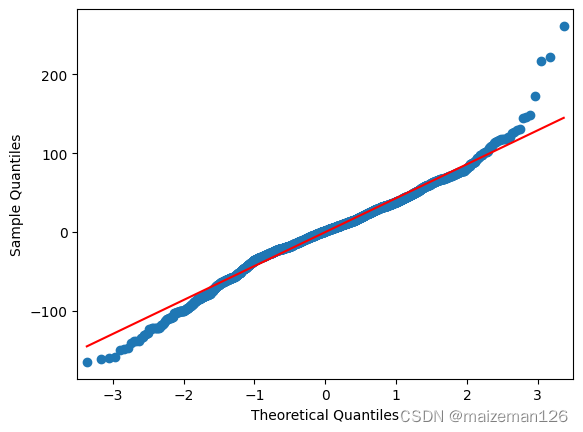
(2)Q-Q图
Q-Q图用于判断数据是否符合某个参考分布。许多模型都假设数据是正态分布的,因此Q-Q图常用于检验数据是否来自正态分布。
如果Q-Q图上的点在红线上,就表示数据符合参考分布,否则要转换数据。
from scipy import stats
resid=house1.resid_deviance.copy()
resid_std=stats.zscore(resid)
fig=statsmodels.graphics.gofplots.qqplot(resid,line='r')
(3)残差直方图
通过绘制残差直方图,观察数据是否呈正态分布。
fig,ax=plt.subplots()
ax=sns.histplot(resid_std,kde=True)
2、比较多个模型
有时需要比较多个模型,以便从中选出“最佳”模型。
(1)比较线性模型
首先拟合5个模型。请注意有些模型使用“+”运算符向模型中添加协变量,有些模型则使用“*”运算符进行添加。当在模型中指定交互时应使用“*”操作符,这意味着交互变量的行为不是彼此独立的,他们的值相互影响,而不是简单地相加。
# 原始住房数据集包含class列
# 使用“class”这个词会引发错误,因为class是python的关键字
# 把列重命名为type
f1="value_per_sq_ft ~ units + sq_ft + boro"
f2="value_per_sq_ft ~ units * sq_ft + boro"
f3="value_per_sq_ft ~ units + sq_ft * boro + type"
f4="value_per_sq_ft ~ units + sq_ft * boro + sq_ft * type"
f5="value_per_sq_ft ~ boro + type"
house1=smf.ols(f1,data=housing).fit()
house2=smf.ols(f2,data=housing).fit()
house3=smf.ols(f3,data=housing).fit()
house4=smf.ols(f4,data=housing).fit()
house5=smf.ols(f5,data=housing).fit()
model_results=pd.concat([house1.params,house2.params,
house3.params,house4.params,house5.params],axis=1).\
rename(columns=lambda x: "house"+str(x+1)).\
reset_index().\
rename(columns={"index":"params"}).\
melt(id_vars='params',var_name='model',value_name='estimate')
print(model_results.head())
查看大量值意义不大,可以把系数绘制出来,直观展现模型是如何估计彼此的相关参数的。
fig,ax=plt.subplots()
ax=sns.pointplot(x='estimate',y='params',hue="model",
data=model_results,
dodge=True,
join=False)
plt.tight_layout()
下面使用方差分析(ANOVA)方法来比较它们。方差分析会给出残差平方和(SSR),可以通过它来评估模型的性能(残差平方和越小,模型的拟合效果越好。)
model_names=['house1','house2','house3','house4','house5']
house_anova=statsmodels.stats.anova.anova_lm(
house1,house2,house3,house4,house5)
house_anova.index=model_names
print(house_anova)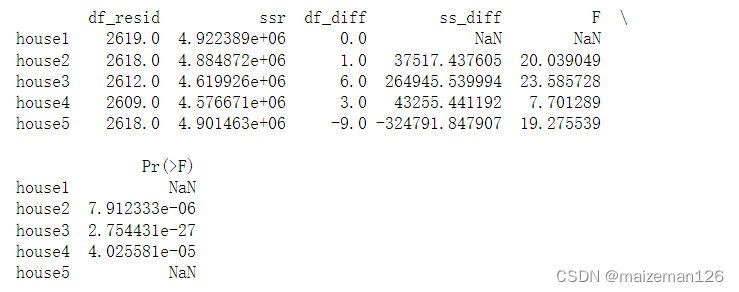
评估模型性能的另一种方法是使用赤池信息量准测(AIC)和贝叶斯信息准备(BIC)。这些方法均引入了与模型参数个数相关的惩罚项。因此,应尽量在模型的性能和简洁性之间做好平衡(简单优于复杂)。
(2)比较GLM
可以采用同样的方法评估和诊断GLM。不过,方差分析只评估模型的偏差。
def anova_deviance_table(*models):
return pd.DataFrame({
'df_residuals':[i.df_resid for i in models],
'resid_stddev':[i.deviance for i in models],
'df':[i.df_model for i in models],
'deviance':[i.deviance for i in models]
})
f1="value_per_sq_ft ~ units + sq_ft + boro"
f2="value_per_sq_ft ~ units * sq_ft + boro"
f3="value_per_sq_ft ~ units + sq_ft * boro + type"
f4="value_per_sq_ft ~ units + sq_ft * boro + sq_ft * type"
f5="value_per_sq_ft ~ boro + type"
glm1=smf.glm(f1,data=housing).fit()
glm2=smf.glm(f2,data=housing).fit()
glm3=smf.glm(f3,data=housing).fit()
glm4=smf.glm(f4,data=housing).fit()
glm5=smf.glm(f5,data=housing).fit()
glm_anova=anova_deviance_table(glm1,glm2,glm3,glm4,glm5)
print(glm_anova)(3)k折交叉验证
较差验证是另一种模型比较方法。它可以解释模型在新数据上的表现。这种方法会把数据分成k个部分,把其中一个部分用作测试集,把其余部分用作训练集来拟合模型。模型拟合好之后,使用测试集进行测试,并计算误差。不断重复这个过程,直到k个部分都测试过。
k通常取值介于 5和10之间。请注意,k值越大,所需要计算的时间越长,请根据实际情况选择合适的k值。